📄 اطبع pdf
00971504825082

🌐 English / الإنجليزية

<<< الحركة الدورانية >>>

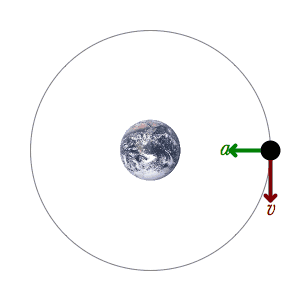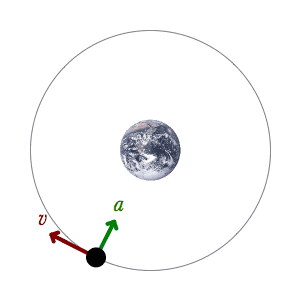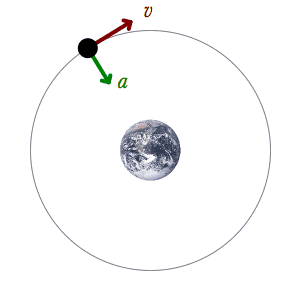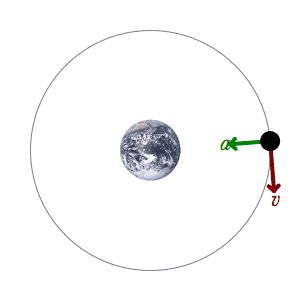
الإزاحة الزاوية

تذكر : الإزاحة الخطية = الموقع النهائي – الموقع الابتدائي

\[∆𝑥=𝑥_2−𝑥_1\]

الإزاحة الزاوية = الزاوية النهائية – الزاوية الابتدائية

\[∆𝜃=𝜃_2−𝜃_1\]

إذا تحرك جسم من نقطة الى اخرى وقطع قوس طوله \[s\] على محيط دائرة نصف قطرها \[r\] فإن الزاوية التي تقابل القوس تسمى بالإزاحة الزاوية ويرمز لها بالرمز \[𝜃\]

\[𝜃 =\frac{s}{r}\]

ملاحظة: الإزاحة الزاوية كمية متجهة. إذا كان الدوران عكس عقارب الساعة تأخذ إشارة موجبة (+)، وإذا كان الدوران مع عقارب الساعة تأخذ إشارة سالبة (-)

الراديان: يمثل الراديان الوحدة لقياس الإحداثيات الزاوية

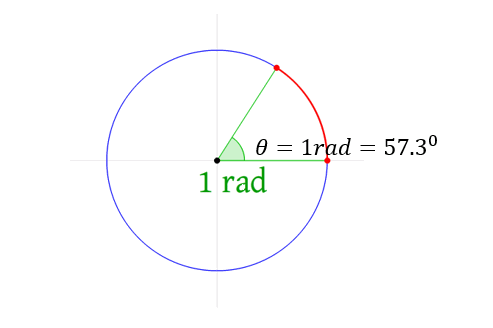
تحويل الوحدات: قد تجد الإزاحة الزاوية بوحدة الدرجات أو بوحدة الدورات (rev). يتم تحويل الزاوية إلى الراديان حسب معاملات التحويل التالية:

معامل التحويل من الدورات إلى الراديان	معامل التحويل من الدرجات إلى الراديان
\[2𝜋 (rad)= 1 rev\]	\[𝜋 (rad )= 180^0\]
مثال: جسم يتحرك حركة دائرية قطع إزاحة زاوية قدرها 2.25 دورة فكم يعادل بالراديان؟	مثال: جسم قطع إزاحة زاوية 120 درجة فكم يعادل بوحدة الراديان؟
\[𝜃 = 2.25 × 2𝜋 =14.13 rad\]	\[𝜃 = 120^0 × \frac{𝜋}{180}=2.1 rad\]

السرعة الزاوية

تذكر: السرعة المتجهة الخطية لجسم ما هي تغير الإحداثيات الخطية للجسم بالنسبة للزمن

السرعة الزاوية لجسم ما: هي تغير الإحداثي الزاوي للجسم مع الزمن

\[W_{avg}=\frac{∆𝜃 (rad)}{∆t (s)}= \frac{𝜃_2 - 𝜃_1}{t_2 -t_1}\]

التجربة 1: قياس السرعة الزاوية

اجعل الحركة الدائرية منتظمة (a𝛾=0.0)

اضغط على الخط البياني (𝜃-t)

الفترة الزمنية	الإزاحة الزاوية النهائية	الإزاحة الزاوية الابتدائية
\[t_2 - t_1= ....s\]	\[𝜃_2= .....rad\]	\[𝜃_1= ....rad\]

السرعة الزاوية	اتجاه السرعة الزاوية
\[W= \frac{𝜃_2 - 𝜃_1}{t_2 -t_1}= ......rad/s\]	إذا كان الدوران عكس عقارب الساعة إذا كان الدوران بإتجاه عقارب الساعة

معلومات مفيدة: السرعة الزاوية والسرعة الخطية

يكون متجه السرعة الخطية مماساً لمحيط الدائرة دائماً ويشير إلى اتجاه الحركة وينطبق على متجه الوحدة المماسي

لاحظ: يكون متجه السرعة الخطية عمودياً دائماً على متجه الموقع القطري

\[\vec r . \vec v = 0\]

يوجد علاقة بين السرعة الخطية والسرعة الزاوية

\[v = r \cdot w\]

\[1 \star\]

يتحرك جسم حركة دورانية منتظمة يعمل دورة واحدة كل ثانية فان سرعته الزاوية بوحدة \[Rad/s\]

أختر الإجابة الصحيحة

---

A

w= 4𝜋 rad/s

B

w= 𝜋 rad/s

C

w= 2𝜋 rad/s

D

w= 3𝜋 rad/s

اضغط هنا تظهر طريقة الحل

\[2 \star\]

مروحة تدور بسرعة زاوية قدرها \[60 𝜋 \; rad/s\] فان الزاوية التي تقطعها أحد شفراتها خلال زمن قدره \[3\;s\] تعادل

أختر الإجابة الصحيحة

---

A

∆𝜃=120 𝜋 rad

B

∆𝜃=60 𝜋 rad

C

∆𝜃=180 𝜋 rad

D

∆𝜃=220 𝜋 rad

\[3 \star\]

مروحة تدور في مسار دائري منتظم نصف قطره \[60\;cm\] حيث تقطع المروحة ثلاث دورات خلال زمن قدره \[2\;s\] فان سرعتها الخطية بوحدة \[m/s\] تعادل

أختر الإجابة الصحيحة

---

A

𝑣 = 3.64 m/s

B

𝑣 = 5.65 m/s

C

𝑣 = 2.41 m/s

D

𝑣 = 6.72 m/s

معلومات مفيدة: العجلة الزاوية

العجلة الزاوية المتوسطة (𝛼): وهي عبارة عن معدل السرعة الزاوية

\[𝛼_\text{avg} = \frac{W_2 - W_1}{t_2 - t_1}\]

وتقدر بوحدة \[\frac{rad}{s^2}\]

العجلة الزاوية للحركة الدائرية تحدث عندما يتحرك الجسم حركة دائرية بسرعة غير ثابتة

هناك علاقة بين العجلة الزاوية والعجلة الخطية

\[a = r \cdot 𝛼\]

التجربة 2: قياس التسارع الزاوي

اجعل الحركة الدائرية غير منتظمة

حرك أيقونة التسارع الزاوي واجعل قيمة للتسارع الزاوي لا تساوي الصفر

اضغط على الخط البياني (w-t)

الفترة الزمنية	السرعة الزاوية النهائية	السرعة الزاوية الابتدائية
\[t_2 - t_1= ....s\]	\[w_2= .....rad/s\]	\[w_1= ....rad/s\]

التسارع الزاوي	العجلة الخطية أو التسارع المماسي
\[𝛼 = a𝛾 = \frac{w_2 - w_1}{t_2 - t_1}= ......\frac{rad}{s^2}\] متوسط التسارع الزاوي = معدل تغير سرعة الزاوية خلال الزمن	(𝑎𝜀= at) اضغط على أيقونة التسارع المماسي راقب اتجاه التسارع المماسي \[a_t = 𝛼 \cdot r = ......\frac{m}{s^2}\] إذا كان لدينا جسم يتحرك بمسار دائري وبسرعة متغيرة هناك تسارع زاوي وبالتالي تسارع خطي

\[4\]

دولاب سيارة يتحرك بسرعة \[10\;\frac{rad}{s}\] غير سرعته فأصبحت \[15\;\frac{rad}{s}\] خلال زمن قدره \[10\;s\] فإن التسارع الزاوي للدولاب يعادل

أختر الإجابة الصحيحة

---

A

𝛼=4 𝑟𝑎𝑑/𝑠²

B

𝛼=2 𝑟𝑎𝑑/𝑠²

C

𝛼=1 𝑟𝑎𝑑/𝑠²

D

𝛼=0.5 𝑟𝑎𝑑/𝑠²

إلعب وتعلم

نتائج مهمة: العلاقة بين الحركة الخطية والحركة الدائرية

الحركة الخطية	الحركة الدائرية
الإزاحة الخطية (s)	الإزاحة الزاوية (θ)
السرعة الخطية (v)	السرعة الزاوية (ω)
العجلة الخطية (a)	العجلة الزاوية (α)

عزم قوة

نقول أن لقوة عزم إذا كانت القوة قادرة على إحداث حركة دورانية لجسم حول محور الدوران. وهو قيمة متجهة لقياس مدى قدرة قوة على تدوير الجسم حول محور ما، على أنه حاصل ضرب القوة بطول الذراع ويدعى العزم.

يرمز لعزم الدوران بالحرف الإغريقي "تاو" (τ)، ووحدته في النظام الدولي للوحدات هي نيوتن متر (N·m).

باستطاعتنا باستخدام قاعدة اليد اليمنى لإيجاد اتجاه متجه عزم الدوران. إذا وضعنا أصابعنا في اتجاه الذراع، وقمنا بلفها باتجاه القوة، سيشير الإبهام باتجاه متجه عزم الدوران.

محاكاة حساب عزم الدوران

القوة (N): ذراع القوة (m): الزاوية (درجة): احسب العزم

\[5 \star\]

في الشكل أدناه قوتين متساويتين أثرت على جسم قابل للدوران فأصبح الجسم يدور فإن أحد الإجابات التالية صحيحة

أختر الإجابة الصحيحة

---

A

𝜏𝐵 > 𝜏𝐴

B

𝜏𝐴 = 𝜏𝐵

C

𝜏𝐴 > 𝜏𝐵

D

لا يوجد إجابة صحيحة

محصلة العزوم

قد يكون هناك أكثر من قوة واحدة تؤثر على جسم ما، كل واحدة من هذه القوى قد تؤثر على الجسم من نقاط مختلفة. ثم إن كل قوة من هذه القوى ستولد عزم دوران على الجسم، ويكون عزم الدوران الكلي مجموع عزوم الدوران الفردية. ويكون اتجاه الدوران باتجاه العزم الأكبر.

مثال: محصلة العزوم

أوجد محصلة العزم. الجسم متأثر بقوتين وقابل للدوران حول محور يقع في مركز الجسم

F₁ = F₂ = 50 N

r₁ = 30 cm, r₂ = 50 cm

الحل:

القوة الأولى مقدارها 50 نيوتن وتبعد 30 سانتي متر عن محور الدوران والقوة تصنع زاوية 90 درجة مع الذراع وتجعل الجسم يدور عكس عقارب الساعة فإن عزمها موجب.

\[𝜏_1 = 𝑟_1 \cdot 𝐹_1 \cdot \sin{𝜃_1} = +0.3 × 50 × \sin{90} = +15 \, N \cdot m\]

القوة الثانية مقدارها 50 نيوتن وتبعد 50 سانتي متر عن محور الدوران والقوة تصنع زاوية 60 درجة مع الذراع وتجعل الجسم يدور مع عقارب الساعة فإن عزمها سالب.

\[𝜏_2 = 𝑟_2 \cdot 𝐹_2 \cdot \sin{𝜃_2} = -0.5 × 50 × \sin{60} = -21.65 \, N \cdot m\]

حساب محصلة العزم الكلي:

\[𝜏_{net} = 𝜏_1 + 𝜏_2 = +15 - 21.65 = -6.65 \, N \cdot m\]

الإشارة السالبة تدل على أن الجسم سوف يدور في النهاية مع عقارب الساعة.

حاسبة محصلة العزوم

قوة 1

القوة (نيوتن): الذراع (متر): الزاوية (درجة): الاتجاه: عكس عقارب الساعة (+) مع عقارب الساعة (-)

إضافة قوة جديدة احسب المحصلة

ملاحظة مهمة: متى ينعدم عزم الدوران لجسم؟

لاحظ: أي قوة تمر بمحور الدوران أو توازي محور الدوران فإن عزمها معدوم.

في هذه المحاكاة يوجد أوزان مختلفة على لعبة الميزان لكل منهما عزم دوران. القوة المؤثرة هي وزن الجسم. في الطرف الأيسر الجسم وزنه ثابت \[F_0=12.5 N\]

نقطة ارتكاز اللعبة هي الوتد

أكمل بيانات الجدول وفي كل مرة طبق على التجربة للتأكد من النتائج

محصلة العزوم \[𝜏_{net}=𝜏_1+𝜏_0\]	عزم القوة على يسار الوتد \[𝜏_0=𝑟_0 \cdot 𝐹_0 \cdot \sin{90}\]	عزم القوة على يمين الوتد \[𝜏_1=𝑟_1 \cdot 𝐹_1 \cdot \sin{90}\]
\[𝜏_{net}=........\]	\[m_1=5 \, Kg, \, r_1=10 \, m\] \[................\]	\[m_2=8 \, Kg, \, r_1=6 \, m\] \[................\]
\[𝜏_{net}=........\]	\[m_1=7 \, Kg, \, r_1=3 \, m\] \[................\]	\[m_2=9 \, Kg, \, r_2=3 \, m\] \[................\]
\[𝜏_{net}=........\]	\[m_1=3 \, Kg, \, r_1=8 \, m\] \[................\]	\[m_2=8 \, Kg, \, r_2=3 \, m\] \[................\]
\[𝜏_{net}=........\]	\[m_1=5 \, Kg, \, r_1=10 \, m\] \[................\]	\[m_2=2 \, Kg, \, r_1=2 \, m\] \[................\]

المصدر: https://www.golabz.eu/lab/circular-motion-9

اكتب تعليقا واذا كان هناك خطأ اكتبه وحدد مكانه Write a comment, and if there is mistake, write and specify its location

No comments:

Post a Comment