Physics
بنك الأسئلة المجال الكهربائي وقانون جاوس |
📄 اطبع pdf
00971504825082
\[1 \star\]
أحد وحدات القياس التالية تكافئ وحدة قياس المجال الكهربائي
أختر الإجابة الصحيحة
A
\[Kg.m.A^{-1}.s^{-2}\]
B
\[Kg.m.A^{-1}.s^{-3}\]
C
\[Kg.m.A^{-1}.s^{-1}\]
D
\[Kg.m.A^{-2}.s^{-2}\]
اضغط هنا تظهر طريقة الحل
\[2\star\]
مجال كهربائي شدته \[E=500\frac{N}{C}\]وضع إلكترون داخل المجال
فإن القوة الكهربائية المؤثرة على الإلكترون تعادل
\[q_e=1.6×10^{-19}C\]
أختر الإجابة الصحيحة
A
\[Fe=4×10^{-17} \;\;N\;\;\;\;\;\;\] عكس اتجاه المجال
B
\[Fe=4×10^{-17} \;\;N\;\;\;\;\;\;\] بإتجاه المجال
C
\[Fe=8×10^{-17} \;\;N\;\;\;\;\;\;\] عكس اتجاه المجال
D
\[Fe=8×10^{-17} \;\;N\;\;\;\;\;\;\] بإتجاه المجال
اضغط هنا تظهر طريقة الحل
\[3 \star \star\]
في الشكل ادناه شحنتين على نفس الخط
\[q_1=+9\;\;nc\;\;\;\;\;\;\;\;q_2=?\]
النقطة \[A\] انعدم عندها المجال الكهربائي فإن مقدار ونوع الشحنة \[q_2\] تعادل
أختر الإجابة الصحيحة
A
\[q_2= + 1.44 ×10^{-7}\;\;c\]
B
\[q_2= + 2.25 ×10^{-7}\;\;c\]
C
\[q_2= - 3.2 ×10^{-7}\;\;c\]
D
\[q_2= -4.5 ×10^{-7}\;\;c\]
اضغط هنا تظهر طريقة الحل
\[4 \star \star\]
في الشكل أدناه تم حساب المجال عند النقطة \[A\]
\[E_{net}=500\frac{N}{C}\]
واتجاهها موضح على الرسم. فإذا كان مقدار المجال الكهربائي
الناتج عن الشحنة الاولى يعادل
\[E_{1}=300\frac{N}{C}\]فإن نوع
ومقدار الشحنة الثانية يعادل
أختر الإجابة الصحيحة
A
\[q_2= - 3.24 ×10^{-9}\;\;c\]
B
\[q_2= + 5.67 ×10^{-9}\;\;c\]
C
\[q_2= - 2.43 ×10^{-9}\;\;c\]
D
\[q_2= + 1.78 ×10^{-9}\;\;c\]
اضغط هنا تظهر طريقة الحل
\[5 \star\]
في الشكل أدناه تم رسم خطوط المجال لثلاث شحنات فإن أحد الاجابات التالية صحيحة
أختر الإجابة الصحيحة
A
\[q_1(+)\;\;\;\;q_2(-)\;\;\;\;q_3(-)\;\;\;\;\;q_1=q_2=q_3\]
B
\[q_1(+)\;\;\;\;q_2(-)\;\;\;\;q_3(-)\;\;\;\;\;q_2>q_1>q_3\]
C
\[q_1(-)\;\;\;\;q_2(+)\;\;\;\;q_3(+) \;\;\;\;\;q_3>q_1>q_2\]
D
\[q_1(+)\;\;\;\;q_2(-)\;\;\;\;q_3(-) \;\;\;\;\;q_1>q_2=q_3\]
اضغط هنا تظهر طريقة الحل
\[6 \star \star\]
(1 ×10-10m) ثنائي قطب البعد بين قطبيه
(0.4 m) تم حساب المجال الناتج عن الثنائي عند نقطه تبعد عن المركز الثنائي وعلى امتداد محور الثنائي مسافة
فكانت شدة المجال \[E= 9×10^{-18}\frac{N}{C}\]فان شحنه الثنائي تعادل
أختر الإجابة الصحيحة
A
\[q= 3.2 ×10^{-19}\;\;c\]
B
\[q= 6.4 ×10^{-19}\;\;c\]
C
\[q= 1.3 ×10^{-19}\;\;c\]
D
\[q= 2.6 ×10^{-19}\;\;c\]
اضغط هنا تظهر طريقة الحل
\[7\star\]
وضع جسيم موجب الشحنة داخل المجال الموضح بالشكل أدناه فإن أحد الإجابات التالية تعبر عن حركة الجسم
أختر الإجابة الصحيحة
A
يتحرك الجسيم بسرعة ثابتة
B
يتحرك الجسيم بعجلة ثابتة
C
يتحرك الجسيم بعجلة متناقصة
D
يتحرك الجسيم بعجلة متزايدة
اضغط هنا تظهر طريقة الحل
\[8 \star \]
تركت كره كتلتها
\[m=5\;kg\] تسقط على الارض و هي مشحونة بشحنه مقدارها
\[q= 5\; µc\] فان متجهه المجال الكهربائي
المنتظم الذي يجعلها متزنة
أختر الإجابة الصحيحة
A
\[E= 9.8×10^3 \;\;N/C\;\;\;\;\downarrow\;\;\;\;\;\;\] نحو الأسفل
B
\[E= 9.8×10^3 \;\;N/C\;\;\;\;\uparrow\;\;\;\;\;\;\] نحو الأعلى
C
\[E= 1×10^3 \;\;N/C\;\;\;\;\downarrow\;\;\;\;\;\;\] نحو الأسفل
D
\[E= 1×10^3 \;\;N/C\;\;\;\;\uparrow\;\;\;\;\;\;\] نحو الأعلى
اضغط هنا تظهر طريقة الحل
\[9 \star \star \star\]
(E=1×103N/C) قذف الكترون داخل منطقه مجال منتظم شدته
و يتجه نحو المحور الرأسي الموجب كما في الشكل أدناه
(𝜗=5×106m/s) و بسرعه مقدارها
(8 Cm) وبشكل أفقي فقطع مسافه مقدارها
على المحور الأفقي فإنه يقطع ازاحه على المحور الرأسي بنفس الفترة الزمنية
أختر الإجابة الصحيحة
A
\[∆𝑌=0.033\;\;m\]
B
\[∆𝑌=0.022\;\;m\]
C
\[∆𝑌=0.011\;\;m\]
D
\[∆𝑌=0.044\;\;m\]
اضغط هنا تظهر طريقة الحل
\[10\star\]
أحد الاشكال التالية يكون عزم الدوران لثنائي القطب معدوم في المجال الكهربائي المنتظم
أختر الإجابة الصحيحة
A
A
B
B
C
C
D
D
اضغط هنا تظهر طريقة الحل
\[11 \star \star \]
( 𝜏= 1.5 × 10-9N.m ) ثنائي القطب اكبر عزم الدوران له
(الموجب z) و يتجه نحو محور
(الموجب y) وهو موضوع في مجال كهربائي منتظم يتجه نحو المحور
( E = 1 × 10-3N/C ) وشدته
أختر الإجابة الصحيحة
B
\[ P=1.5×10^{-8} \;\;c.m\;\;\;\;\;\;-A\] باتجاه المحور الأفقي الموجب
A
\[P=1.5×10^{-6} \;\;c.m\;\;\;\;\;\;-C\] باتجاه المحور الأفقي الموجب
C
\[P=1.5×10^{-8} \;\;c.m\;\;\;\;\;\;-D\] باتجاه المحور الأفقي السالب
D
\[P=1.5×10^{-6} \;\;c.m\;\;\;\;\;\;-B\] باتجاه المحور الأفقي السالب
اضغط هنا تظهر طريقة الحل
\[12 \star \star \star\]
(0.3 m) سلك طوله لا نهائي تم حساب المجال عند نقطة تبعد عن السلك
(2.5 × 103N/C) فكانت قيمة المجال الكهربائي
والاتجاه موضح على الشكل فإن عدد الالكترونات المكتسبة أو المفقودة في وحدة الطول تعادل
أختر الإجابة الصحيحة
A
\[n=2.6×10^{11}\;\;\;\;\;\;\] إكتسب إلكترونات
B
\[n=2.6×10^{11}\;\;\;\;\;\;\] فقد إلكترونات
C
\[n=3.4×10^{11}\;\;\;\;\;\;\] إكتسب إلكترونات
D
\[n=3.4×10^{11}\;\;\;\;\;\;\] فقد إلكترونات
اضغط هنا تظهر طريقة الحل
\[13 \star \star\]
أحد الوحدات التالية هي وحدة قياس التدفق الكهربائي
أختر الإجابة الصحيحة
A
\[Kg.m .A^{-1}.S^{-3}\]
B
\[Kg.m^2 .A^{-1}.S^{-2}\]
C
\[Kg.m^3 .A^{-1}.S^{-3}\]
D
\[Kg.m^2 .A^{-1}.S^{-3}\]
اضغط هنا تظهر طريقة الحل
\[14 \star\]
قشره كرويه مشحونة بشحنه قدرها
\[-4\;\;µc\] وضع بداخلها شحنه
\[+4\;\;µc\] فان الشحنة الداخلية
\[q_1=?\]
و الخارجية للقشرة الكروية \[q_2=?\]
على التتابع
أختر الإجابة الصحيحة
A
\[q_1=+4\;µc \;\;\;\;\;q_2=+4\;µc\]
B
\[q_1=0.0 \;\;\;\;\;q_2=0.0\]
C
\[q_1=-4\;µc \;\;\;\;\;q_2=+4\;µc\]
D
\[q_1=-4\;µc \;\;\;\;\;q_2=0.0\]
اضغط هنا تظهر طريقة الحل
\[15 \star \star\]
( A ) سلكان لا نهائيان في الطول كثافة الشحنات و الأبعاد موضحة بالشكل أدناه فإن النقطة
لها شدة مجال تعادل
أختر الإجابة الصحيحة
A
\[ E= 4200 \;\;N/C\;\;\;\;\;\longrightarrow\;\;\;\;\;\;\] نحو اليمين
B
\[ E= 2800 \;\;N/C\;\;\;\;\;\longleftarrow \;\;\;\;\;\;\] نحو اليسار
C
\[E= 4800 \;\;N/C\;\;\;\;\;\longrightarrow\;\;\;\;\;\;\] نحو اليمين
D
\[E= 3500 \;\;N/C\;\;\;\;\;\longleftarrow\;\;\;\;\;\;\] نحو اليسار
اضغط هنا تظهر طريقة الحل
\[16 \star\]
لوحان لا نهائيان في الطول موصلين تم شحنهما بكثافة متساوية. أحد الإجابة التالية صحيحة
أختر الإجابة الصحيحة
A
\[EA=EC=0 \;\;\;\;\;, \;\;\;\;\;EB=ED≠0\]
B
\[EA>EC \;\;\;\;\;, \;\;\;\;\;EB=ED\]
C
\[ EA=EB=EC=ED \]
D
\[ EA=EB \;\;\;\;\;, \;\;\;\;\;ED=EC\]
اضغط هنا تظهر طريقة الحل
\[17 \star\star\]
لوحان لا نهائيان غير موصولين يمتلكان نفس الشحنة.
تم حساب المجال الكهربائي عند النقطة
\[A\] فكانت شدته \[E= 1×10^3\frac{N}{C}\] فان كثافة
الشحنة على كل لوح تعادل
أختر الإجابة الصحيحة
A
\[𝛿= 3.6 ×10^{-9} \;\;c/m^2\]
B
\[𝛿= 8.85×10^{-9} \;\;c/m^2\]
C
\[𝛿= 4.8×10^{-9} \;\;c/m^2\]
D
\[𝛿= 3.9×10^{-8} \;\;c/m^2\]
اضغط هنا تظهر طريقة الحل
\[18 \star\star\]
ثلاث شحن متساوية في المقدار والنوع
وضعت على رؤوس مثلث متساوي الأضلاع
( 12 N ) كما في الشكل ادناه تم حساب القوة المتبادلة بين شحنتين فكانت
فإن محصلة القوى المؤثرة على أي شحنة تعادل
أختر الإجابة الصحيحة
A
\[F_{net}=24 \;\; N\]
B
\[F_{net}=16.65 \;\; N\]
C
\[F_{net}=10.39 \;\; N\]
D
\[F_{net}=20.87 \;\; N\]
اضغط هنا تظهر طريقة الحل
\[19 \star \star \star\]
قشره كرويه غير مشحونة نصف قطرها الداخلي
\[0.5 \;m\] نصف قطرها الخارجي
\[0.7 \;m\] وضع داخلها كما في الشكل أدناه شحنة نقطية مقدارها
\[-6\;µc\] في مركزها فان شده المجال عند نقطه تبعد
\[0.6\;m\]
أختر الإجابة الصحيحة
A
\[ E = 2.3 ×10^5 \;\;N/C \]
B
\[ E = 4.6 ×10^5 \;\;N/C \]
C
\[ E=0.0 \]
D
\[ E = 1.5 ×10^5 \;\;N/C \]
اضغط هنا تظهر طريقة الحل
\[20 \star \star\]
تم رسم العلاقة بين المجال والبعد عن سطح موصل كروي أجوف
فنتج الخط البياني التالي فان الموصل مشحون بشحنة قدرها
أختر الإجابة الصحيحة
A
\[q= 1.34×10^{-19} \;\;c\]
B
\[q= 1.78×10^{-19} \;\;c\]
C
\[q= 2.56×10^{-19} \;\;c\]
D
\[q= 2.14×10^{-19} \;\;c\]
اضغط هنا تظهر طريقة الحل
\[21 \star \star \star\]
تم رسم العلاقة بين المجال والبعد عن مركز كرة مشحونة
مصمته غير موصلة فكان الخط البياني التالي فان مقدار المجال عند
نقطة تبعد عن مركز الكرة
(0.15 m) مسافة
تعادل
أختر الإجابة الصحيحة
A
\[E=2800 \;\;N/C\]
B
\[E=3000 \;\;N/C\]
C
\[E=2700 \;\;N/C\]
D
\[E=2900 \;\;N/C\]
اضغط هنا تظهر طريقة الحل
\[22\star \star \star\]
تم رسم العلاقة بين المجال والبعد عن مركز كرة مشحونة بشكل منتظم و
مصمته غير موصلة فكان الخط البياني التالي فان مقدار الشحنة الموجودة في
(0.1 m) كرة نصف قطرها
موجودة داخل الكرة المشحونة تعادل
أختر الإجابة الصحيحة
A
\[q= 2.45×10^{-9} \;\;c\]
B
\[q= 1.78×10^{-9} \;\;c\]
C
\[q= 7.45×10^{-9} \;\;c\]
D
\[q= 2.2×10^{-9} \;\;c\]
اضغط هنا تظهر طريقة الحل
\[23\star \star \star\]
كرة مصمتة غير موصلة مشحونة بشكل منتظم نصف قطرها
\[R=0.5\;\; m\]تم حساب المجال عند نقطة تبعد عن مركز الكرة \[r=0.3\;\; m\]
فكانت قيمته \[E=4×10^3\frac{N}{C}\]فان شحنة الكرة تعادل
أختر الإجابة الصحيحة
A
\[q= 5.71×10^{-6} \;\;c\]
B
\[q= 6.28×10^{-6} \;\;c\]
C
\[q= 3.54×10^{-6} \;\;c\]
D
\[q= 1.85×10^{-6} \;\;c\]
اضغط هنا تظهر طريقة الحل
\[24\star \star \star\]
قشرة كروية شحنتها
\[-7 \;\;µc \] نصف قطرها الداخلي
\[2 \;\;m\] والخارجي
\[4\;\;M\] تم حساب المجال عند نقطة تبعد عن مركزها فكانت شدة المجال
\[E= 3 ×10^3\;\;N/C\]واتجاهه نحو القشرة فان الشحنة الموجودة داخل القشرة الكروية تعادل
أختر الإجابة الصحيحة
A
\[q= +5.33 ×10^{-6} \;\;c\]
B
\[q= -5.33×10^{-6} \;\;c\]
C
\[q= +1.67×10^{-6} \;\;c\]
D
\[q= -1.67 ×10^{-6} \;\;c\]
اضغط هنا تظهر طريقة الحل
\[25 \star \star\]
شحنة كهربائية تولد حولها مجال كهربائي
تم حساب المجال الكهربائي عند النقطة
\[A\] فكانت شدة المجال تعادل \[ E= 6×10^4\;\;N/C \]
تم حساب المجال الكهربائي عند النقطة
\[B\] فكانت شدة المجال تعادل
\[ E= 3×10^4\;\;N/C \] فإن النسبة بين بعد النقطة
\[\frac{r_A}{r_B}\] تعادل
أختر الإجابة الصحيحة
A
\[\frac{r_A}{r_B}=0.4\]
B
\[\frac{r_A}{r_B}=0.7\]
C
\[\frac{r_A}{r_B}=0.5\]
D
\[\frac{r_A}{r_B}=0.25\]
اضغط هنا تظهر طريقة الحل
\[26 \star\]
في الشكل أدناه شحنة نقطية تولد حولها مجال كهربائي فإن
النسبة بين مجال النقطة
\[A\] إلى مجال النقطة
\[B\]
تعادل
أختر الإجابة الصحيحة
A
\[\frac{E_A}{E_B}=16\]
B
\[\frac{E_A}{E_B}=3\]
C
\[\frac{E_A}{E_B}=9\]
D
\[\frac{E_A}{E_B}=4\]
اضغط هنا تظهر طريقة الحل
\[27 \star\]
يوضح في الشكل أربعة من أسطح جاوس تحيط بتوزيع الشحنات .أي سطح جاوس لا يوجد بها تدفق كهربائي من خلال الشكل أدناه
أختر الإجابة الصحيحة
A
السطح الأول
B
السطح الثاني
C
السطح الثالث
D
السطح الرابع
اضغط هنا تظهر طريقة الحل
\[28 \star\]
يتم وضع سطح جاوس على شكل حبة الفاصولياء في أربع مناطق مختلفة من المجال الكهربائي. هذا موضح بخطوط المجال أدناه
في أي حالة يكون التدفق الكهربائي الكلي أعلى من خلال السطح المغلق
أختر الإجابة الصحيحة
A
اA
B
B
C
C
D
D
اضغط هنا تظهر طريقة الحل
\[29 \star\]
(+4q) شحنة نقطية موجبة
(-3q) وضعت داخل كرة موصلة
وتم وضع شحنة نقطية سالبة خارج الكرة ومقدارها
أحد الإجابات التالية تعبر بشكل صحيح عن نتائج قانون جاوس
أختر الإجابة الصحيحة
A
الشحنة الموجودة خارج الموصل تؤثر بقوة أكبر على الشحنة داخل الموصل
B
الشحنة الموجودة داخل الموصل تؤثر بقوة أكبر على الشحنة خارج الموصل
C
كلا الشحنتين يؤثر بنفس القوة ولكن باتجاه متعاكس
D
الشحنة داخل الموصل لن تتأثر بقوة و الشحنة خارج الموصل تتأثر بقوة
اضغط هنا تظهر طريقة الحل
\[30 \star\]
(∅=3 ×102N.m2/c) وضعت شحنة داخل سطح كروي وتم حساب التدفق
على السطح فكانت قيمته
إذا تم مضاعفة نصف قطر السطح الكروي فإن التدفق على السطح الجديد
يكون
أختر الإجابة الصحيحة
A
\[∅= 6 ×10^2 \;\;N.m^2/C\]
B
\[∅= 3×10^2 \;\;N.m^2/C\]
C
\[∅= 12 ×10^2 \;\;N.m^2/C\]
D
\[∅= 1.5 ×10^2 \;\;N.m^2/C\]
اضغط هنا تظهر طريقة الحل
\[31 \star \star\]
مجال كهربائي شدته تعطى بالعلاقه \[E=8\hat{X}+3\hat{Y}+4\hat{Z}(\frac{N.m^2}{c})\]
(10 Cm) فإن التدفق عبر سطح الجانبي الأيمن للمكعب طول ضلعة
أختر الإجابة الصحيحة
A
\[∅= 6 ×10^{-2} \;\;N.m^2/C\]
B
\[∅= 8 ×10^{-2 }\;\;N.m^2/C\]
C
\[∅= 2 ×10^{-2} \;\;N.m^2/C\]
D
\[∅= 4×10^{-2} \;\;N.m^2/C\]
اضغط هنا تظهر طريقة الحل
\[32 \star\]
كرة موصلة مجوفة نصف قطرها
\[0.2\;\;m\] تم شحنها بشكل منتظم حيث فقدت الكرة عدد من الالكترونات قدره
\[n= 5×10^{12}\] إلكترون فإن كثافة الشحنات على سطح الموصل تعادل
علما بأن \[q_e=1.6×10^{-19} c\]
أختر الإجابة الصحيحة
A
\[𝛿= 1.6 ×10^{-6} \;\;c/m^2\]
B
\[𝛿= 6 ×10^{-6} \;\;c/m^2\]
C
\[𝛿= 3.6 ×10^{-6} \;\;c/m^2\]
D
\[𝛿= 4.8 ×10^{-6} \;\;c/m^2\]
اضغط هنا تظهر طريقة الحل
\[33 \star\]
( 0.1 m ) شبه اسطوانة مصنوعة من مادة عازلة نصف قطر قاعدتها الصغيرى
\[0.1\;\;m\]
ونصف قطر قاعدتها الكبرى
\[0.2\;\;m\] تم وضعها في مجال مجال كهربائي منظم كما في الشكل أدناه شدته
\[500\;\;N/C\] فإن التدفق الذي يجتاز السطح الجانبي لشبه الاسطوانة يعادل
أختر الإجابة الصحيحة
A
\[∅=0.0\]
B
\[∅= - 35.2 \;\;N.m^2/C\]
C
\[∅=47.1 \;\;N.m^2/C\]
D
\[∅= 25.3\;\;N.m^2/C\]
اضغط هنا تظهر طريقة الحل
\[34 \star\]
مكعب وضع في مركزه شحنة نقطية مقدارها
\[8 ×10^{-9}c\] فإن التدفق على السطح العلوي والسفلي يعادل
\[ 𝓔_0=8.85 ×10^{-12}C.m/v\]
أختر الإجابة الصحيحة
A
\[∅=151 \;\;N.m^2 \;\;\;\;\;\;-A\]
B
\[∅= 301 \;\;N.m^2/C\;\;\;\;\;\;-B\]
C
\[∅=432 \;\;N.m^2/C\;\;\;\;\;\;-C\]
D
\[∅=512\;\;N.m^2/C\;\;\;\;\;\;-D\]
اضغط هنا تظهر طريقة الحل
حل المسائل التالية
\[1\star\]
شحنتين نقطيتين على استقامة واحدة
مقدار كل منهما \[q_1=8\;\;nc\;\;\;\;\;\;\;\;\;\; q_2=?\]تم حساب المجال الكهربائي عند النقطة
\[A\]فكانت مقداره يعادل
\[E_{net}=500 \;\;N/C\]من خلال معلومات الشكل والبيانات السابقة
ما نوع \[q_2\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
احسب مقدار الشحنة \[q_2\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
اضغط هنا تظهر طريقة الحل
\[2\star\]
كرة نخاع بيلسان كتلتها
\[m=5 \;\;g\]مشحونة علقت بخيط لا يمتط وثبت الخيط في السقف تم وضعها داخل مجال كهربائي منتظم شدته
\[E=1×10^3 \;\;N/C\]فانحرفت الكرة نحو اليمين كما في الشكل
بحيث يصنع الخيط مع المحور الرأسي زاوية مقدارها
\[𝜃=8^0\]
حدد نوع شحنة الكرة
\[........................................................................................\]
\[........................................................................................\]
احسب مقدار شحنة الكرة
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
اضغط هنا تظهر طريقة الحل
\[3\star\]
موصل كروي نصف قطره
\[R=0.05 \;\; m\]
يتم توزيع على السطح، كمية من الشحنة بالتساوي بكثافة شحنة سطحية قدرها
\[𝜎=8.5\;\;nc/m^2\]احسب المجال الكهربي عند سطح هذا الموصل
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
اضغط هنا تظهر طريقة الحل
\[4\star\]
قشره كرويه
نصف قطرها الخارجي والداحلي \[R_1=0.5 \;\;m \;\;\;\;\;\;\;R_2=0.8 \;\;m \]
وشحنة القشرة
\[6\;\;µc\]وضع داخلها في المركز شحنه
\[-4\;\;µc\]
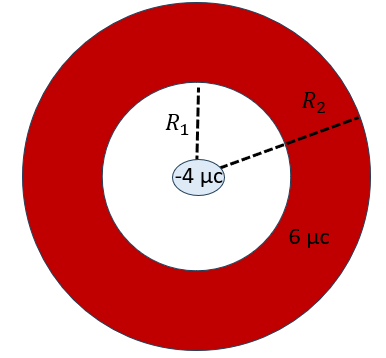
احسب المجال على بعد
\[r_1=0.4\;\;m\] من مركز القشرة
\[...................................\;\;\;\;\;\;\;...................................\]
\[...................................\;\;\;\;\;\;\;...................................\]\[...................................\;\;\;\;\;\;\;...................................\]
احسب المجال على بعد
\[r_2=0.7\;\;m\] من مركز القشرة
\[...................................\;\;\;\;\;\;\;...................................\]
\[...................................\;\;\;\;\;\;\;...................................\]\[...................................\;\;\;\;\;\;\;...................................\]
احسب المجال على بعد
\[r_3=1\;\;m\] من مركز القشرة
\[...................................\;\;\;\;\;\;\;...................................\]
\[...................................\;\;\;\;\;\;\;...................................\]\[...................................\;\;\;\;\;\;\;...................................\]
اضغط هنا تظهر طريقة الحل
\[5\star\]
مكعب طول ضلعة
\[0.3\;\;m\]
وضع داخل مجال كهربائي منتظم يتجه نحو محور الأفقي الموجب
شدته \[E=200\frac{N}{C}\]أحسب التدفق الذي يجتاز كل سطح والتدفق الكلي
اضغط هنا تظهر طريقة الحل
\[6\star\]
مكعب تم وضع 12 بروتون داخل المكعب و13 نترون وعدد من الإلكترونات
تم قياس التدفق الكهربائي على المكعب فكانت قيمته
\[∅=9.05×10^{-8}\;N.m^2/c\]
احسب مقدار الشحنة الموجودة داخل المكعب
مع العلم أن
\[𝜀_0=8.85×10^{−12}\;c^2/N.m^2\]
اضغط هنا تظهر طريقة الحل
🧮 Calculator
🗑️
✏️ قلم
أحد وحدات القياس التالية تكافئ وحدة قياس المجال الكهربائي
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
مجال كهربائي شدته \[E=500\frac{N}{C}\]وضع إلكترون داخل المجال فإن القوة الكهربائية المؤثرة على الإلكترون تعادل \[q_e=1.6×10^{-19}C\]
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
في الشكل ادناه شحنتين على نفس الخط
\[q_1=+9\;\;nc\;\;\;\;\;\;\;\;q_2=?\]
النقطة \[A\] انعدم عندها المجال الكهربائي فإن مقدار ونوع الشحنة \[q_2\] تعادل
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
في الشكل أدناه تم حساب المجال عند النقطة \[A\]
\[E_{net}=500\frac{N}{C}\]
واتجاهها موضح على الرسم. فإذا كان مقدار المجال الكهربائي
الناتج عن الشحنة الاولى يعادل
\[E_{1}=300\frac{N}{C}\]فإن نوع
ومقدار الشحنة الثانية يعادل
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
في الشكل أدناه تم رسم خطوط المجال لثلاث شحنات فإن أحد الاجابات التالية صحيحة
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
(1 ×10-10m) ثنائي قطب البعد بين قطبيه
(0.4 m) تم حساب المجال الناتج عن الثنائي عند نقطه تبعد عن المركز الثنائي وعلى امتداد محور الثنائي مسافة
فكانت شدة المجال \[E= 9×10^{-18}\frac{N}{C}\]فان شحنه الثنائي تعادل
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
وضع جسيم موجب الشحنة داخل المجال الموضح بالشكل أدناه فإن أحد الإجابات التالية تعبر عن حركة الجسم
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
تركت كره كتلتها \[m=5\;kg\] تسقط على الارض و هي مشحونة بشحنه مقدارها \[q= 5\; µc\] فان متجهه المجال الكهربائي المنتظم الذي يجعلها متزنة
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
(E=1×103N/C) قذف الكترون داخل منطقه مجال منتظم شدته
و يتجه نحو المحور الرأسي الموجب كما في الشكل أدناه
(𝜗=5×106m/s) و بسرعه مقدارها
(8 Cm) وبشكل أفقي فقطع مسافه مقدارها
على المحور الأفقي فإنه يقطع ازاحه على المحور الرأسي بنفس الفترة الزمنية
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
أحد الاشكال التالية يكون عزم الدوران لثنائي القطب معدوم في المجال الكهربائي المنتظم
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
( 𝜏= 1.5 × 10-9N.m ) ثنائي القطب اكبر عزم الدوران له
(الموجب z) و يتجه نحو محور
(الموجب y) وهو موضوع في مجال كهربائي منتظم يتجه نحو المحور
( E = 1 × 10-3N/C ) وشدته
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
(0.3 m) سلك طوله لا نهائي تم حساب المجال عند نقطة تبعد عن السلك
(2.5 × 103N/C) فكانت قيمة المجال الكهربائي
والاتجاه موضح على الشكل فإن عدد الالكترونات المكتسبة أو المفقودة في وحدة الطول تعادل
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
أحد الوحدات التالية هي وحدة قياس التدفق الكهربائي
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
قشره كرويه مشحونة بشحنه قدرها \[-4\;\;µc\] وضع بداخلها شحنه \[+4\;\;µc\] فان الشحنة الداخلية \[q_1=?\] و الخارجية للقشرة الكروية \[q_2=?\] على التتابع
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
( A ) سلكان لا نهائيان في الطول كثافة الشحنات و الأبعاد موضحة بالشكل أدناه فإن النقطة
لها شدة مجال تعادل
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
لوحان لا نهائيان في الطول موصلين تم شحنهما بكثافة متساوية. أحد الإجابة التالية صحيحة
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
لوحان لا نهائيان غير موصولين يمتلكان نفس الشحنة. تم حساب المجال الكهربائي عند النقطة \[A\] فكانت شدته \[E= 1×10^3\frac{N}{C}\] فان كثافة الشحنة على كل لوح تعادل
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
ثلاث شحن متساوية في المقدار والنوع
وضعت على رؤوس مثلث متساوي الأضلاع
( 12 N ) كما في الشكل ادناه تم حساب القوة المتبادلة بين شحنتين فكانت
فإن محصلة القوى المؤثرة على أي شحنة تعادل
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
قشره كرويه غير مشحونة نصف قطرها الداخلي \[0.5 \;m\] نصف قطرها الخارجي \[0.7 \;m\] وضع داخلها كما في الشكل أدناه شحنة نقطية مقدارها \[-6\;µc\] في مركزها فان شده المجال عند نقطه تبعد \[0.6\;m\]
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
تم رسم العلاقة بين المجال والبعد عن سطح موصل كروي أجوف فنتج الخط البياني التالي فان الموصل مشحون بشحنة قدرها
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
تم رسم العلاقة بين المجال والبعد عن مركز كرة مشحونة
مصمته غير موصلة فكان الخط البياني التالي فان مقدار المجال عند
نقطة تبعد عن مركز الكرة
(0.15 m) مسافة
تعادل
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
تم رسم العلاقة بين المجال والبعد عن مركز كرة مشحونة بشكل منتظم و
مصمته غير موصلة فكان الخط البياني التالي فان مقدار الشحنة الموجودة في
(0.1 m) كرة نصف قطرها
موجودة داخل الكرة المشحونة تعادل
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
كرة مصمتة غير موصلة مشحونة بشكل منتظم نصف قطرها
\[R=0.5\;\; m\]تم حساب المجال عند نقطة تبعد عن مركز الكرة \[r=0.3\;\; m\]
فكانت قيمته \[E=4×10^3\frac{N}{C}\]فان شحنة الكرة تعادل
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
قشرة كروية شحنتها \[-7 \;\;µc \] نصف قطرها الداخلي \[2 \;\;m\] والخارجي \[4\;\;M\] تم حساب المجال عند نقطة تبعد عن مركزها فكانت شدة المجال \[E= 3 ×10^3\;\;N/C\]واتجاهه نحو القشرة فان الشحنة الموجودة داخل القشرة الكروية تعادل
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
شحنة كهربائية تولد حولها مجال كهربائي تم حساب المجال الكهربائي عند النقطة \[A\] فكانت شدة المجال تعادل \[ E= 6×10^4\;\;N/C \] تم حساب المجال الكهربائي عند النقطة \[B\] فكانت شدة المجال تعادل \[ E= 3×10^4\;\;N/C \] فإن النسبة بين بعد النقطة \[\frac{r_A}{r_B}\] تعادل
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
في الشكل أدناه شحنة نقطية تولد حولها مجال كهربائي فإن النسبة بين مجال النقطة \[A\] إلى مجال النقطة \[B\] تعادل
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
يوضح في الشكل أربعة من أسطح جاوس تحيط بتوزيع الشحنات .أي سطح جاوس لا يوجد بها تدفق كهربائي من خلال الشكل أدناه
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
يتم وضع سطح جاوس على شكل حبة الفاصولياء في أربع مناطق مختلفة من المجال الكهربائي. هذا موضح بخطوط المجال أدناه
في أي حالة يكون التدفق الكهربائي الكلي أعلى من خلال السطح المغلق
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
(+4q) شحنة نقطية موجبة
(-3q) وضعت داخل كرة موصلة
وتم وضع شحنة نقطية سالبة خارج الكرة ومقدارها
أحد الإجابات التالية تعبر بشكل صحيح عن نتائج قانون جاوس
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
(∅=3 ×102N.m2/c) وضعت شحنة داخل سطح كروي وتم حساب التدفق
على السطح فكانت قيمته
إذا تم مضاعفة نصف قطر السطح الكروي فإن التدفق على السطح الجديد
يكون
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
مجال كهربائي شدته تعطى بالعلاقه \[E=8\hat{X}+3\hat{Y}+4\hat{Z}(\frac{N.m^2}{c})\]
(10 Cm) فإن التدفق عبر سطح الجانبي الأيمن للمكعب طول ضلعة
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
كرة موصلة مجوفة نصف قطرها \[0.2\;\;m\] تم شحنها بشكل منتظم حيث فقدت الكرة عدد من الالكترونات قدره \[n= 5×10^{12}\] إلكترون فإن كثافة الشحنات على سطح الموصل تعادل علما بأن \[q_e=1.6×10^{-19} c\]
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
( 0.1 m ) شبه اسطوانة مصنوعة من مادة عازلة نصف قطر قاعدتها الصغيرى \[0.1\;\;m\] ونصف قطر قاعدتها الكبرى \[0.2\;\;m\] تم وضعها في مجال مجال كهربائي منظم كما في الشكل أدناه شدته \[500\;\;N/C\] فإن التدفق الذي يجتاز السطح الجانبي لشبه الاسطوانة يعادل
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
مكعب وضع في مركزه شحنة نقطية مقدارها \[8 ×10^{-9}c\] فإن التدفق على السطح العلوي والسفلي يعادل \[ 𝓔_0=8.85 ×10^{-12}C.m/v\]
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
حل المسائل التالية
شحنتين نقطيتين على استقامة واحدة مقدار كل منهما \[q_1=8\;\;nc\;\;\;\;\;\;\;\;\;\; q_2=?\]تم حساب المجال الكهربائي عند النقطة \[A\]فكانت مقداره يعادل \[E_{net}=500 \;\;N/C\]من خلال معلومات الشكل والبيانات السابقة ما نوع \[q_2\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
احسب مقدار الشحنة \[q_2\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
اضغط هنا تظهر طريقة الحل
كرة نخاع بيلسان كتلتها
\[m=5 \;\;g\]مشحونة علقت بخيط لا يمتط وثبت الخيط في السقف تم وضعها داخل مجال كهربائي منتظم شدته
\[E=1×10^3 \;\;N/C\]فانحرفت الكرة نحو اليمين كما في الشكل
بحيث يصنع الخيط مع المحور الرأسي زاوية مقدارها
\[𝜃=8^0\]
حدد نوع شحنة الكرة
\[........................................................................................\]
\[........................................................................................\]
احسب مقدار شحنة الكرة
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
اضغط هنا تظهر طريقة الحل
موصل كروي نصف قطره \[R=0.05 \;\; m\] يتم توزيع على السطح، كمية من الشحنة بالتساوي بكثافة شحنة سطحية قدرها \[𝜎=8.5\;\;nc/m^2\]احسب المجال الكهربي عند سطح هذا الموصل
اضغط هنا تظهر طريقة الحل
قشره كرويه نصف قطرها الخارجي والداحلي \[R_1=0.5 \;\;m \;\;\;\;\;\;\;R_2=0.8 \;\;m \] وشحنة القشرة \[6\;\;µc\]وضع داخلها في المركز شحنه \[-4\;\;µc\]
اضغط هنا تظهر طريقة الحل
مكعب طول ضلعة
\[0.3\;\;m\]
وضع داخل مجال كهربائي منتظم يتجه نحو محور الأفقي الموجب
شدته \[E=200\frac{N}{C}\]أحسب التدفق الذي يجتاز كل سطح والتدفق الكلي
اضغط هنا تظهر طريقة الحل
مكعب تم وضع 12 بروتون داخل المكعب و13 نترون وعدد من الإلكترونات
تم قياس التدفق الكهربائي على المكعب فكانت قيمته
\[∅=9.05×10^{-8}\;N.m^2/c\]
احسب مقدار الشحنة الموجودة داخل المكعب
مع العلم أن
\[𝜀_0=8.85×10^{−12}\;c^2/N.m^2\]
اضغط هنا تظهر طريقة الحل
جزاكم الله عنا خير الجزاء
ReplyDeleteوإياكم إن شاء الله
ReplyDelete