📄 اطبع pdf
00971504825082

<<<تطبيقات المجالات الكهربائية >>>

اضغط هنا تظهر نواتج التعلم

جواب	سؤال
الكرة كلما اقتربت من سطح الأرض تقل طاقة الوضع الجذبية فهي غير قادرة على العودة إلى موقعها	ماذا يحدث لطاقة الوضع لكرة عندما نرفع الكرة عن سطح الأرض
عندما نحرك شحنة موجبة باتجاه المجال تقل طاقة الوضع الكهربائية فهي غير قادرة على العودة إلى موقعها	ماذا يحدث لطاقة الوضع الكهربائية لشحنة موجبة عندما يتم تحريكها باتجاه المجال
عندما نحرك شحنة سالبة عكس اتجاه المجال تقل طاقة الوضع الكهربائية فهي غير قادرة على العودة إلى موقعها دون تأثير قوى خارجية	ماذا يحدث لطاقة الوضع الكهربائية لشحنة سالبة عندما يتم تحريكها بعكس اتجاه المجال
عندما نحرك شحنة سالبة باتجاه المجال تزداد طاقة الوضع الكهربائية فهي قادرة على العودة إلى موقعها	ماذا يحدث لطاقة الوضع الكهربائية لشحنة سالبة عندما يتم تحريكها باتجاه المجال
عندما نحرك شحنة موجبة عكس اتجاه المجال تزداد طاقة الوضع الكهربائية فهي قادرة على العودة إلى موقعها دون تأثير قوى خارجية	ماذا يحدث لطاقة الوضع الكهربائية لشحنة موجبة عندما يتم تحريكها بعكس اتجاه المجال

أكمل بيانات الجدول التالي

التغير في طاقة الوضع الكهربائية	اتجاه حركة الشحنة	نوع الشحنة
\[...........\]	بإتجاه المجال	موجبة
\[...........\]	عكس المجال	موجبة

\[...........\]	بإتجاه المجال	سالبة
\[...........\]	عكس المجال	سالبة

إظهار الحل

الحل الكامل:

التغير في طاقة الوضع الكهربائية	اتجاه حركة الشحنة	نوع الشحنة
تنقص	بإتجاه المجال	موجبة
تزداد	عكس المجال	موجبة

تزداد	بإتجاه المجال	سالبة
تنقص	عكس المجال	سالبة

فرق الجهد بين نقطتين

هو عبارة عن جهد النقطة النهائية مطروح منها جهد النقطة البدائية

( B و A ) عندما يطلب أحسب فرق الجهد بين النقطتين

ينم حسابها بالشكل التالي \[ ∆ 𝑉_{𝐴𝐵}=𝑉_B - 𝑉_A\]

والجهد عند نقطة هو عبارة عن طاقة الوضع التي تختزنها وحدة الشحن عند تلك النقطة أي عندما يطلب حساب الجهد عند نقطة داخل مجال كهربائي نضع شحنة اختبار عند تلك النقطة ونحدد طاقة الوضع الكهربائية التي تختزنها شحنة الاختبار عند تلك النقطة ونقسم على شحنة الاختبار \[∆ 𝑉_{𝐴𝐵}=\frac{PE_B}{q}-\frac{PE_A}{q}=\frac{∆PE_{AB}}{q}\]

\[∆PE_{AB}= W_{A→B} \] هنا الشغل المبذول في تحيك الشحنة من نقطة البداية إلى نقطة النهاية بوساطة قوة خارجية لو تم استخدام قوة داخلية في بذل الشغل نضيف للعلاقة السابقة إشارة سالب حتى تتحقق المساواة \[ ∆ 𝑉_{𝐴𝐵}= \frac{ W_{A→B}}{q}\]

متى يكون فرق الجهد بين نقطتين موجب ومتى يكون سالب ومنى يكون معدوم

(∆𝑉𝐴𝐵 ) في الشكل أدناه متى فرق الجهد

موجب أم سالب أم معدوم

للإجابة نضع شحنة اختبار موجبة أو سالبة عند نقطة البداية
ويتم نقلها إلى نقطة النهاية بوساطة قوة خارجية التي هي معاكسة للقوة الداخلية
فإذا كانت القوة الخارجية باتجاه الإزاحة فإن الشغل المبذول موجب أي أكبر من الصفر
وإذا كانت القوة الخارجية عكس الإزاحة فإن الشغل المبذول سالب أي أصغر من الصفر
وإذا كانت القوة عمودية على الإزاحة فإن الشغل معدوم ثم نطبق العلاقة مع الأخذ بعين الاعتبار نوع شحنة الاختبار
\[ ∆ 𝑉_{𝐴𝐵}= \frac{ W_{A→B}}{q}\]يكون فرق الجهد موجب عندما \[ ∆ 𝑉_{𝐴𝐵}>0\] يكون فرق الجهد سالب عندما \[ 0>∆ 𝑉_{𝐴𝐵}\] يكون فرق الجهد معدوم عندما \[ ∆ 𝑉_{𝐴𝐵}=0\]

تجربة قياس فرق الجهد بين نقطتين
قم بإختيار نوع الشحنة المولدة للمجال حرك مقياس الجهد إلى الموقع المطلوب قياس جهده
غير الموقع وانظرإلى القياس مره أخرى وحدد الفرق


قم بقياس الجهد للنقاط التي لها نفس البعد عن الشحنة ماذا تستنتج
..................................................................
قم بقياس الجهد لعدد من النقاط بإتجاه المجال ماذا تستنتج
..................................................................

اضغط هنا تظهر النتائج المطلوبة

قياس فرق الجهد بين نقطتين في مجال منتظم

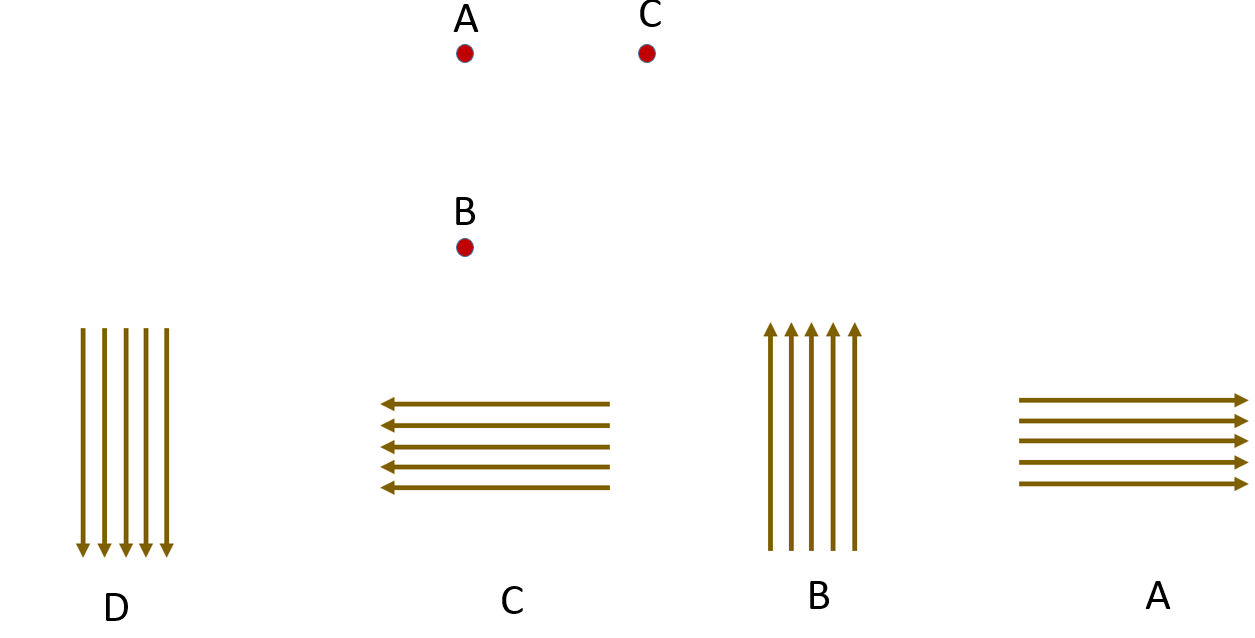
أي من الأشكال أدناه يمثل مجال منتظم وايهما يمثل مجال غير منتظم

من صفات المجال المنتظم هو مجال ثابت المقدار والاتجاه عند جميع النقاط خطوطه مستقيمة متوازية تبعد نفس البعد عن بعضها البعض


تجربة قياس فرق الجهد بين لوحي مكثف مجال منتظم




(1.5 V ) فرق الجهد يعادل
(1.5 V ) جهد اللوح الموجب
(0 V ) جهد اللوح السالب

عند قياس فرق الجهد بين لوح المكثف السالب والنقطة \[A\] فرق الجهد يعادل \[V=1(V)\] جهد النقطة \[1(V)\] جهد اللوح السالب \[V^-=0.0(V)\] عند قياس فرق الجهد بين لوح المكثف السالب والنقطة \[B\] فرق الجهد يعادل \[V=0.5(V)\] جهد اللوح السالب \[V^-=0.0(V)\]
(C) عند قياس فرق الجهد بين لوح المكثف السالب والنقطة \[C\]
(0.5 V ) فرق الجهد يعادل بين لوح المكثف السالب والنقطة \[V=0.5 (V)\] جهد اللوح السالب \[V^-=0.0(V)\]
نستنتج أن \[V^+=1.5 \;V\;\;\;\;\;V_A=1\;V\;\;\;\;\;V_B=0.5\;V\;\;\;\;\;V_C=0.5\;V\;\;\;\;\;V^-=0.0\;V\]

اضغط هنا تظهر النتائج المطلوبة

يعطى فرق الجهد في مجال كهربائي منتظم بالعلاقة \[ ∆V_{AB}= E . d \]
E قوة المجال الكهربائي
d=0.3m الازاحة الموازية لخطوط المجال

\[1 \star\]

ثلاث نقاط داخل مجال منتظم كما في الشكل أدناه أحد الخطوط تمثل الشكل الصحيح لخطوط المجال المنتظم علما بأن \[ V_A=8V , V_B=6V , V_C=8V \]

أختر الإجابة الصحيحة

---

A

A

B

B

C

C

D

D

اضغط هنا تظهر طريقة الحل

\[2 \star\]

في الشكل أدناه مجال كهربائي منتظم شدته \[E=1000\frac{N}{C}\] فإن فرق الجهد بين النقطتين \[∆𝑉_{𝑎 𝑑} \]
تعادل

أختر الإجابة الصحيحة

---

A

\[ ∆V= 200\;\; V \]

B

\[ ∆V= 300\;\; V \]

C

\[ ∆V= 400\;\; V \]

D

\[ ∆V= 600\;\; V \]

اضغط هنا تظهر طريقة الحل

تجربة مليكان

تجربة ميليكان لتحديد الشحنة الأولية

في سنة 1909 توصل “روبرت ميليكان”، أستاذ بجامعة شيكاغو، وبمساعدة من الأستاذ هارفي فليتشر إلى القيمة التقريبية للشحنة الإبتدائية للإلكترون. تسمى الطريقة التي اعتمدها ميليكان تجربة قطرات الزيت المشحونة

اعتمدت التجربة على دراسة قطرات الزيت المشحونة في مجال كهربائي:

الهدف من التجربة

تحديد شحنة الإلكترون عن طريق دراسة حركة قطرات الزيت في مجال كهربائي.

\[ q =\frac { (m × g)}{ E }\]
حيث:

المفهوم	الرمز	الوصف
الكتلة	m	كمية المادة في الجسم (واحدة القياس: كيلوجرام)
شحنة القطرة	q	الشحنة الكهربائية للقطرة (واحدة القياس: كولوم)
شدة المجال الكهربائي	E	قوة المجال الكهربائي المؤثر على الشحنة (واحدة القياس: نيوتن/كولوم)
عجلة الجاذبية الأرضية	g	تسارع الجسم تحت تأثير الجاذبية (واحدة القياس: م/ث²)

الاستنتاج

عندما تكون القوة الكهربائية مساوية للقوة الجاذبية

\[ qE = mg \] \[ q = \frac{mg}{E} \]

بعد تكرار التجربة، لوحظ أن الشحنة \[q\] دائماً ما تكون مضاعفات عدد صحيح لشحنة أساسية \[ e \]

\[ q = ne \]

حيث \[ n = 1, 2, 3, ... \]

تم تحديد قيمة الشحنة الأساسية (شحنة الإلكترون)

\[ e \approx 1.602 \times 10^{-19} \, \text{C} \]

حاسبة شحنة قطرة الزيت (تجربة مليكان)

المسافة بين اللوحين (متر):

فرق الجهد (فولت):

كثافة القطرة (كجم/م³):

حجم القطرة (م³):

احسب الشحنة

في هذه المحاكاة هي نسخة مبسطة من تجربة قام بها روبرت مليكان ، برش قطرات زيت متأينة قليلاً في مجال كهربائي وتم ملاحظة القطرات وتم تغير الجهد حتى تصبح القطرة متزنة وتكون القوة الكهربائية تعادل وزن القطرة



من خلال التجربة التالية أجب عن الأسئلة

\[ ..................... \] اضغط هنا تظهر طريقة الحل	قطرة الزيت المشحونة بشحنة موجبة ما هو سبب اتجاه حركتها نحو الارض
\[ ...................... \] اضغط هنا تظهر طريقة الحل	عند دخول القطرة الصندوق المشحون حدد اتجاه المجال الكهربائي وما هي القوى المتأثرة بها
\[ ..................... \] اضغط هنا تظهر طريقة الحل	ما هي العلاقة التي يتم من خلالها حساب شدة المجال داخل الصندوق
\[ ...................... \] اضغط هنا تظهر طريقة الحل	غير ملكان شدة المجال الكهربائي حتى أصبحت القطرة متزنة استنتج العلاقة التي يتم من خلالها حساب شحنة القطرة

اكتب تعليقا واذا كان هناك خطأ اكتبه وحدد مكانه Write a comment, and if there is mistake, write and specify its location

No comments:

Post a Comment