Physics
📄 اطبع pdf
00971504825082
المجال الكهربائي
اضغط هنا تظهر نواتج التعلم
Click here to view the learning outcomes
االمجال الكهربائي
هي منطقة تحيط بالشحنة وتظهر فيها أثار القوة الكهربائية
وهو عبارة عن محصلة القوة الكهربائية المؤثرة على شحنة مقسوما على الشحنة
و المجال الكهربائي كمية متجهه لها مقدار واتجاه
\[\vec E=\frac{\vec F_e}{q}= \frac{\frac{K.Q.q}{r^2}}{q}=\frac{K.Q}{r^2} \]
تحديد الاتجاه هناك طريقتتين
الطريقة الأولى
:نضع شحنة أختبار عند النقطة المطلوب تحديد الاتجاه عندها وحسب قواعد المتجهات حاصل ضرب عدد في متجه
فإذا تم وضع شحنة موجبة فإن اتجاه المجال بنفس اتجاه القوة وإذا كانت شحنة الأختبار سالبة فإن اتجاه المجال عكس اتجاه القوة الكهربائية
تحديد اتجاه المجال الكهربائي
تجربة تفاعلية لتحديد اتجاه المجال الكهربائي
شرح التجربة:
1. يتم تحديد شحنة المصدر (موجبة أو سالبة) باستخدام الأزرار أدناه
2. انقر على لوحة الرسم لوضع شحنة الاختبار (سيتم سؤالك عن نوعها)
3. سيظهر اتجاه القوة المؤثرة على شحنة الاختبار واتجاه المجال الكهربائي
4. إذا كانت شحنة الاختبار موجبة، فإن اتجاه المجال بنفس اتجاه القوة
5. إذا كانت شحنة الاختبار سالبة، فإن اتجاه المجال عكس اتجاه القوة
الطريقة الثانية : من خلال رسم خطوط المجال لشحنة موجبة ولشحنة سالبة
خطوط المجال لشحنة موجبة خارجة من الشحنة
خطوط المجال لشحنة سالبة داخلة على الشحنة
تجربة خطوط المجال الكهربائي
تجربة خطوط المجال الكهربائي
شرح التجربة
خطوط المجال الكهربائي هي خطوط وهمية تستخدم لتمثيل المجال الكهربائي حول الشحنات.
لشحنة موجبة: خطوط المجال تخرج من الشحنة في جميع الاتجاهات (خارجة من الشحنة).
لشحنة سالبة: خطوط المجال تدخل إلى الشحنة من جميع الاتجاهات (داخلة على الشحنة).
شحنة موجبة (+)
شحنة سالبة (-)
\[1 \star\]
أحد وحدات القياس التالية تكافئ وحدة قياس المجال الكهربائي
أختر الإجابة الصحيحة
A
\[Kg.m.A^{-1}.s^{-2}\]
B
\[Kg.m.A^{-1}.s^{-3}\]
C
\[Kg.m.A^{-1}.s^{-1}\]
D
\[Kg.m.A^{-2}.s^{-2}\]
اضغط هنا تظهر طريقة الحل
\[2 \star\]
مجال كهربائي شدته \[E=500\frac{N}{C}\]وضع إلكترون داخل المجال
فإن القوة الكهربائية المؤثرة على الإلكترون تعادل
\[q_e=1.6×10^{-19}C\]
أختر الإجابة الصحيحة
A
\[Fe=4×10^{-17} \;\;N\;\;\;\;\;\;\] عكس اتجاه المجال
B
\[Fe=4×10^{-17} \;\;N\;\;\;\;\;\;\] بإتجاه المجال
C
\[Fe=8×10^{-17} \;\;N\;\;\;\;\;\;\] عكس اتجاه المجال
D
\[Fe=8×10^{-17} \;\;N\;\;\;\;\;\;\] بإتجاه المجال
اضغط هنا تظهر طريقة الحل
تخطيط االمجال الكهربائي
صفات خطوط المجال الكهربائي
هي خطوط وهمية تخرج من الشحنات الموجبة وتدخل في الشحنات السالبة
تناسب كثافة خطوط المجال طردياً مع مقدار الشحنة الكهربائية
اتجاه المجال عن أي نقطة هو المماس لخط المجال عند تلك النقطة
خطوط المجال الكهربائي لا تتقاطع
يوجد نوعين من المجال الكهربائي
مجال منتظم وهو مجال ثايت المقدار والاتجاه عند جميع النقاط خطوطه مستيمة متوازية
مجال غير منتظم وهو مجال غير ثابت المقدار أو الاتجاه أو كلاهما معا
الجال الكهربائي الناتج عن الشحنات النقطية
وجدنا سابقا بأن مقدار المجال الكهربائي لشحنة نقطية يعطى بالعلاقة \[\vec E=\frac {\vec F_e}{q}=\frac {K.Q}{r^2}\]
كل شحنة نقطية تولد حولها مجال كهربائي
فإذا كان لدينا أكثر من شحنة فإن كل شحنة تولد حولها مجال له مقدار و اتجاه
مثال محلول
شحنتين نقطيتين
\[q_1 = -6 \;\;𝜇c \;\;\;\;\;\;\;\; q_2 = 4 \;\;𝜇c\]وضعت الشحنة الأولى عند نقطة الأصل
و وضعت الشحنة الثانية عند الموضع \[X=5\;\;cm\]احسب المجال الكهربائي عند الموضع \[X=8\;\;cm\]
الحل
\[E_1=K.\frac {q_1}{r_1^2}=8.99×10^9×\frac {6×10^{-6}}{0.08^2}=8.43×10^6\;\; N/c\] نحو اليسار
\[E_2=K.\frac {q_2}{r_2^2}=8.99×10^9×\frac {4×10^{-6}}{0.03^2}=39.95×10^6\;\; N/c\] نحواليمين
\[E_{net}=E_2-E_1=39.95×10^6-8.43×10^6=31.52×10^6\]نحواليمين
مثال محلول
شحنتين نقطيتين
\[q_1 = -3 \;\;nc \;\;\;\;\;\;\;\; q_2 = 5 \;\;nc\]وضعت على رؤس مثلث كما في الشكل
احسب المجال الكهربائي عند الموضع
\[A\]
الحل
\[E_1=K.\frac {q_1}{r_1^2}=8.99×10^9×\frac {3×10^{-9}}{0.03^2}=29.9×10^3\;\; N/c\] نحو اليسار
\[E_2=K.\frac {q_2}{r_2^2}=8.99×10^9×\frac {5×10^{-9}}{0.04^2}=28.1×10^3\;\; N/c\] نحو الأسفل
\[E_{net}=\sqrt {E_2^2+E_1^2}=\sqrt {(29.9×10^3)^2+(28.1×10^3)^2}=41.1×10^3\;\;N/C\]الاتجاه \[\theta=tan^{-1}\frac{E_2}{E_1}=tan^{-1}(\frac{28.1×10^3}{29.9×10^3})=43.2.2^0\]
(قراءة ذاتية ) المجال الكهربائي لثنائي القطب
ثنائي القطب :هو جسم مشحون بشحنتين متساويتين في المقدار مختلفتين في النوع
عندما يطلب حساب المجال الكهربائي لثنائي القطب الناتج عن شحنتين مختلفتين
يتم حساب المجال الناتج عن كل شحنة ويتم الجمع الاتجاهي حسب قواعد المتجهات
مثال محلول
حساب المجال الناتج عن ثنائي القطب على امتداد المحور للثنائي عند نقطة تبعد عن مركز الثنائي
(X) مسافة قدرها
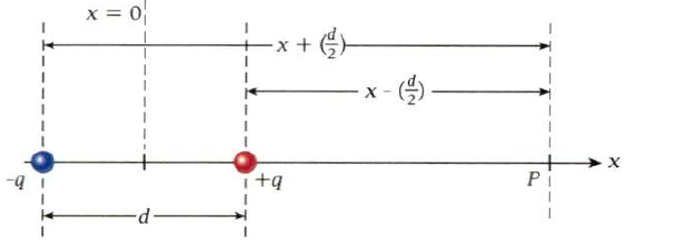
النقطة خاضعة لمجالين من الشحنة الموجبة
\[E_1=\frac{1}{4𝜋ع_0}\frac{q}{(X-\frac{1}{2}d)^2}\] والاتجاه نحو اليمين
من الشحنة السالبة
\[E_2=\frac{1}{4𝜋ع_0}\frac{q}{(X+\frac{1}{2}d)^2}\] والاتجاه نحو اليسار
فتكون المحصلة\[E_{net}=E_1-E_2\]
\[E_1>E_2\]
\[E_{net}=\frac{1}{4𝜋ع_0}\frac{q}{(X-\frac{1}{2}d)^2}-\frac{1}{4𝜋ع_0}\frac{q}{(X+\frac{1}{2}d)^2}\]
والاتجاه نحو اليمين
بإخراج العامل المشترك\[\frac{q}{4𝜋ع_0X^2}\]
تصبح العلاقة \[E_{net}=\frac{q}{4𝜋ع_0X^2}[\frac{1}{(1-\frac{d}{2X})^2}-\frac{1}{(1+\frac{d}{2X})^2}]\] بتوحيد المقامات \[E_{net}=\frac{q}{4𝜋ع_0X^2}[\frac{(1+\frac{d}{2X})^2-(1-\frac{d}{2X})^2}{(1-\frac{d}{2X})^2(1+\frac{d}{2X})^2}]\]
\[E_{net}=\frac{q}{4𝜋ع_0X^2}[\frac{(1+\frac{d}{X}+\frac{d^2}{4X^2})-(1-\frac{d}{X}+\frac{d^2}{4X^2})}{(1-\frac{d}{2X})^2(1+\frac{d}{2X})^2}]\]
\[E_{net}=\frac{q}{4𝜋ع_0X^2}[\frac{(1+\frac{d}{X}+\frac{d^2}{4X^2}-1+\frac{d}{X}-\frac{d^2}{4X^2})}{(1-\frac{d}{2X})^2(1+\frac{d}{2X})^2}]\]
X>>d إذا كان
\[\frac{d}{2X}=0.0\]\[E_{net}=\frac{2dq}{4𝜋ع_0X^3}=\frac{dq}{2𝜋ع_0X^3}=\frac{2kdq}{X^3}\]
\[P=q.d\]يدعى عزم ثنائي القطب وهو كمية متجهه واتجاهه من الشحنة السالبة إلى الموجبة عكس المجال الكهربائي
فتكتب قيمة المجال \[E_{net}=\frac{2p}{4𝜋ع_0X^3}=\frac{p}{2𝜋ع_0X^3}=\frac{2kp}{X^3}\]
مثال محلول
حساب المجال الناتج عن ثنائي القطب عند نقطة تقع على العمود المنصف و تبعد عن مركز الثنائي
(y) مسافة قدرها
النقطة خاضعة لمجالين \[E_1,E_2\] عند تحليل المجال الناتج عن كل شحنة الى مركبتين نلاحظ من خلال التناظر
\[𝐸_{1y} = {𝐸_2y}\]المحصلة لهما تساوي الصفر
من خلال الشكل \[r=\sqrt{(\frac{d}{2})^2+y^2}, Cos 𝜃= \frac{\frac{d}{2}}{r}\]
\[E_{1X}=E_1. Cos 𝜃=\frac{k.q}{r^2}.\frac{\frac{d}{2}}{r}=\frac{k.q}{(\frac{d}{2})^2+y^2}.\frac{\frac{d}{2}}{\sqrt{(\frac{d}{2})^2+y^2}}\]
\[𝐸_{1x} =\frac{kqd}{2[{(\frac{d}{2})^2+y^2}]^{3/2}}\]
\[E_{2X}=E_2. Cos 𝜃=\frac{k.q}{r^2}.\frac{\frac{d}{2}}{r}=\frac{k.q}{(\frac{d}{2})^2+y^2}.\frac{\frac{d}{2}}{\sqrt{(\frac{d}{2})^2+y^2}}\]
\[𝐸_{2x} =\frac{kqd}{2[{(\frac{d}{2})^2+y^2}]^{3/2}}\]
\[E_{net}=𝐸_{1x}+𝐸_{2x}=\frac{kqd}{2[{(\frac{d}{2})^2+y^2}]^{3/2}}+\frac{kqd}{2[{(\frac{d}{2})^2+y^2}]^{3/2}}\]
\[E_{net}= -\frac{kqd}{[{(\frac{d}{2})^2+y^2}]^{3/2}}\]
الإشارة السالبة تعني باتجاه المجور الأفقي السالب
(y>> d) اذا كانت
\[\frac{d}{2}≈
0\]
\[E_{net}= -\frac{kqd}{x^3} \]
التوزيعات العامة للشحنات
إذا كان لدينا عدد كبير جدا من الشحنات وطلب حساب المجال الناتج عنها لا يمكن إيجاد المحصلة
بالطريقة السابقة نستخدم التكامل لإيجاد المحصلة بشرط الشحنات موزعة بشكل منتظم
نأخذ جزء صغير من شحنة الجسم
\[dq\]
ونحسب مجالها ثم نجري التكامل على كامل الجسم
هناك مشكلة إذا كانت الشحنة موزعة على طول جسم أو سطح جسم او على حجم جسم
على طول خط
\[𝑑𝑞=λ𝑑𝑥\]
على مساحة سطح
\[𝑑𝑞=𝛿𝑑A\]
على حجم جسم
\[𝑑𝑞=𝜌𝑑V\]
( اثرائي ) مثال محلول
سلك طولة محدود ومشحون بشكل منتظم كما في الشكل أدناه
أحسب مقدار واتجاه المجال عند نقطة تقع على امتداد الخط المقام
من منتصف السلك
نأخذ شحنة صغيرة
\[dq\]ونحسب مجالها ثم نجري التكامل
على كامل السلك
لو أخذنا نصف السلك ومن خلال التناظر نلاحظ مع
النصف الاخر
\[E_1X=E_2X\]
وتعاكسها في الاتجاه اذا محصلتها صفر
أما المركبة الرأسية للمجال والناتج من كل طرف من السلك فهما متساويان في المقدار وبنفس الاتجاه
\[ d𝐸_1Y =d 𝐸_1 Cos 𝜃 , d𝐸_2Y =d 𝐸_2 Cos 𝜃\]
لذلك لحساب قيمه المجال نحسب مقدار لنصف طول السلك ونضاعف القيمة فنحصل على قيمة المجال
.
من الشكل \[r=\sqrt{X^2+Y^2}, Cos 𝜃= \frac{Y}{r}\]
\[E=2\int_{{\,0}}^{{\,a}}{dE_Y}=2\int_{{\,0}}^{{\,a}}{k\frac{dq}{r^2}Cos 𝜃}=2k\int_{{\,0}}^{{\,a}}{\frac{λ𝑑𝑥}{r^2}\frac{Y}{r}}\]
\[E=2kλY\int_{{\,0}}^{{\,a}}{\frac{{𝑑𝑥}}{({X^2+Y^2})^{3/2}}}\]
والتكامل يتم إنجازه بوساطة الجداول
\[\int_{{\,0}}^{{\,a}}{\frac{{𝑑𝑥}}{({X^2+Y^2})^{3/2}}}=|\frac{1}{Y^2}\frac{X}{\sqrt{X^2+Y^2}}|_{{\,0}}^{{\,a}}=\frac{1}{Y^2}\frac{a}{\sqrt{a^2+Y^2}}\]
\[E=2kλY\frac{1}{Y^2}\frac{a}{\sqrt{a^2+Y^2}}\]
فيكون قيمة المجال الناتج عن سلك طولة محدود
\[E=2kλ\frac{1}{Y}\frac{a}{\sqrt{a^2+Y^2}}\] هي طول نصف السلك : a
حالة خاصة
إذا كان السلك طوله لانهائي فإن a→∞\[\frac{a}{\sqrt{a^2+Y^2}}→1\]
\[E=\frac{2kλ}{y}\]
القوة الناتجة عن المجال الكهربائي
إذا تم وضع شحنة داخل مجال كهربائي
فإن الجسيم سوف يتأثر بقوة كهربائية
\[\vec F_e=q.\vec E\]
إذا كانت الشحنة الموضوعة داخل المجال موجبة فإنها سوف تتحرك بإتجاه المجال وإذا كانت الشحنة سالبة فإنها سوف تتحرك عكس المجال
التجربة التالية توضح القوة الكهربائية المؤثرة على شحنة إختبار وضعت داخل مجال كهربائي
وحركة شحنة الاختبار عند وضعها داخل مجال كهربائي اضغط على ايقونة التشغيل وشاهد اتجاه الحركة وهو نفسه اتجاه القوة ويمكن ان تغير نوع الشحنه المولدة للمجال ومقدارها
وبالامكان تحديد اتجاه المجال بالضغط على ايقونة المجال
حدد اتجاه ومقدار القوة المؤثرة على إلكترون وضع داخل مجال في الحالات التالية
المجال غير منتظم
المجال منتظم
\[F_e= .....................N \]
اضغط هنا تظهر طريقة الحل
\[F_e= .....................N \]
اضغط هنا تظهر طريقة الحل
\[3 \star\]
وضع جسيم موجب الشحنة داخل المجال الموضح بالشكل أدناه فإن أحد الإجابات التالية تعبر عن حركة الجسم
أختر الإجابة الصحيحة
A
يتحرك الجسيم بسرعة ثابتة
B
يتحرك الجسيم بعجلة ثابتة
C
يتحرك الجسيم بعجلة متزايدة
D
يتحرك الجسيم بعجلة متناقصة
اضغط هنا تظهر طريقة الحل
\[4 \star\]
تركت كره كتلتها
\[m=5\;kg\] تسقط على الارض و هي مشحونة بشحنه مقدارها
\[q= 5\; µc\] فان متجهه المجال الكهربائي
المنتظم الذي يجعلها متزنة
أختر الإجابة الصحيحة
A
\[E= 9.8×10^3 \;\;N/C\;\;\;\;\downarrow\;\;\;\;\;\;\] نحو الأسفل
B
\[E= 9.8×10^3 \;\;N/C\;\;\;\;\uparrow\;\;\;\;\;\;\] نحو الأعلى
C
\[E= 1×10^3 \;\;N/C\;\;\;\;\downarrow\;\;\;\;\;\;\] نحو الأسفل
D
\[E= 1×10^3 \;\;N/C\;\;\;\;\uparrow\;\;\;\;\;\;\] نحو الأعلى
اضغط هنا تظهر طريقة الحل
(اثرائي ) ثنائي القطب في مجال كهربائي
عند وضع ثنائي القطب داخل مجال منتظم فإن كل من الشحنتين
تتأثر بقوة كهربائية مما يؤدي إلى دوران ثنائي القطب
وبالتالي ينتج لدينا عزم دوران
لو تم اعتبار محور الدوران عند أحد الشحنتين فإننا نحصل
على عزم دوران
\[ 𝜏 = r . F . Sin 𝜃 \]
r=d وهي البعد بين القطبين
F=q.E القوة المؤثرة على أحد القطبين
𝜃 هي الزاوية بين الذراع والقوة
فنحصل على العلاقة
\[ 𝜏 = q.d. E . Sin 𝜃 \]
\[ 𝜏 = p. E . Sin 𝜃 \]
🧮 Calculator
🗑️
✏️ قلم
المجال الكهربائي |
اضغط هنا تظهر نواتج التعلم
Click here to view the learning outcomes
االمجال الكهربائي
هي منطقة تحيط بالشحنة وتظهر فيها أثار القوة الكهربائية وهو عبارة عن محصلة القوة الكهربائية المؤثرة على شحنة مقسوما على الشحنة
و المجال الكهربائي كمية متجهه لها مقدار واتجاه \[\vec E=\frac{\vec F_e}{q}= \frac{\frac{K.Q.q}{r^2}}{q}=\frac{K.Q}{r^2} \]
تحديد الاتجاه هناك طريقتتين
الطريقة الأولى :نضع شحنة أختبار عند النقطة المطلوب تحديد الاتجاه عندها وحسب قواعد المتجهات حاصل ضرب عدد في متجه
فإذا تم وضع شحنة موجبة فإن اتجاه المجال بنفس اتجاه القوة وإذا كانت شحنة الأختبار سالبة فإن اتجاه المجال عكس اتجاه القوة الكهربائية
تجربة تفاعلية لتحديد اتجاه المجال الكهربائي
شرح التجربة:
1. يتم تحديد شحنة المصدر (موجبة أو سالبة) باستخدام الأزرار أدناه
2. انقر على لوحة الرسم لوضع شحنة الاختبار (سيتم سؤالك عن نوعها)
3. سيظهر اتجاه القوة المؤثرة على شحنة الاختبار واتجاه المجال الكهربائي
4. إذا كانت شحنة الاختبار موجبة، فإن اتجاه المجال بنفس اتجاه القوة
5. إذا كانت شحنة الاختبار سالبة، فإن اتجاه المجال عكس اتجاه القوة
الطريقة الثانية : من خلال رسم خطوط المجال لشحنة موجبة ولشحنة سالبة
خطوط المجال لشحنة موجبة خارجة من الشحنة خطوط المجال لشحنة سالبة داخلة على الشحنة
تجربة خطوط المجال الكهربائي
شرح التجربة
خطوط المجال الكهربائي هي خطوط وهمية تستخدم لتمثيل المجال الكهربائي حول الشحنات.
لشحنة موجبة: خطوط المجال تخرج من الشحنة في جميع الاتجاهات (خارجة من الشحنة).
لشحنة سالبة: خطوط المجال تدخل إلى الشحنة من جميع الاتجاهات (داخلة على الشحنة).
شحنة موجبة (+)
شحنة سالبة (-)
أحد وحدات القياس التالية تكافئ وحدة قياس المجال الكهربائي
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
مجال كهربائي شدته \[E=500\frac{N}{C}\]وضع إلكترون داخل المجال فإن القوة الكهربائية المؤثرة على الإلكترون تعادل \[q_e=1.6×10^{-19}C\]
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
تخطيط االمجال الكهربائي
صفات خطوط المجال الكهربائي
هي خطوط وهمية تخرج من الشحنات الموجبة وتدخل في الشحنات السالبة
تناسب كثافة خطوط المجال طردياً مع مقدار الشحنة الكهربائية
اتجاه المجال عن أي نقطة هو المماس لخط المجال عند تلك النقطة
خطوط المجال الكهربائي لا تتقاطع
يوجد نوعين من المجال الكهربائي
مجال منتظم وهو مجال ثايت المقدار والاتجاه عند جميع النقاط خطوطه مستيمة متوازية
مجال غير منتظم وهو مجال غير ثابت المقدار أو الاتجاه أو كلاهما معا
الجال الكهربائي الناتج عن الشحنات النقطية
وجدنا سابقا بأن مقدار المجال الكهربائي لشحنة نقطية يعطى بالعلاقة \[\vec E=\frac {\vec F_e}{q}=\frac {K.Q}{r^2}\]
كل شحنة نقطية تولد حولها مجال كهربائي
فإذا كان لدينا أكثر من شحنة فإن كل شحنة تولد حولها مجال له مقدار و اتجاه
مثال محلول
شحنتين نقطيتين
\[q_1 = -6 \;\;𝜇c \;\;\;\;\;\;\;\; q_2 = 4 \;\;𝜇c\]وضعت الشحنة الأولى عند نقطة الأصل
و وضعت الشحنة الثانية عند الموضع \[X=5\;\;cm\]احسب المجال الكهربائي عند الموضع \[X=8\;\;cm\]
الحل
\[E_1=K.\frac {q_1}{r_1^2}=8.99×10^9×\frac {6×10^{-6}}{0.08^2}=8.43×10^6\;\; N/c\] نحو اليسار
\[E_2=K.\frac {q_2}{r_2^2}=8.99×10^9×\frac {4×10^{-6}}{0.03^2}=39.95×10^6\;\; N/c\] نحواليمين
\[E_{net}=E_2-E_1=39.95×10^6-8.43×10^6=31.52×10^6\]نحواليمين
مثال محلول
شحنتين نقطيتين
\[q_1 = -3 \;\;nc \;\;\;\;\;\;\;\; q_2 = 5 \;\;nc\]وضعت على رؤس مثلث كما في الشكل
احسب المجال الكهربائي عند الموضع
\[A\]
المجال غير منتظم المجال منتظم \[F_e= .....................N \]
\[F_e= .....................N \]
وضع جسيم موجب الشحنة داخل المجال الموضح بالشكل أدناه فإن أحد الإجابات التالية تعبر عن حركة الجسم أختر الإجابة الصحيحة
تركت كره كتلتها
\[m=5\;kg\] تسقط على الارض و هي مشحونة بشحنه مقدارها
\[q= 5\; µc\] فان متجهه المجال الكهربائي
المنتظم الذي يجعلها متزنة
أختر الإجابة الصحيحة عند وضع ثنائي القطب داخل مجال منتظم فإن كل من الشحنتين
تتأثر بقوة كهربائية مما يؤدي إلى دوران ثنائي القطب
وبالتالي ينتج لدينا عزم دوران
لو تم اعتبار محور الدوران عند أحد الشحنتين فإننا نحصل
على عزم دوران
\[ 𝜏 = r . F . Sin 𝜃 \]
الحل
\[E_1=K.\frac {q_1}{r_1^2}=8.99×10^9×\frac {3×10^{-9}}{0.03^2}=29.9×10^3\;\; N/c\] نحو اليسار
\[E_2=K.\frac {q_2}{r_2^2}=8.99×10^9×\frac {5×10^{-9}}{0.04^2}=28.1×10^3\;\; N/c\] نحو الأسفل
\[E_{net}=\sqrt {E_2^2+E_1^2}=\sqrt {(29.9×10^3)^2+(28.1×10^3)^2}=41.1×10^3\;\;N/C\]الاتجاه \[\theta=tan^{-1}\frac{E_2}{E_1}=tan^{-1}(\frac{28.1×10^3}{29.9×10^3})=43.2.2^0\]
(قراءة ذاتية ) المجال الكهربائي لثنائي القطب
ثنائي القطب :هو جسم مشحون بشحنتين متساويتين في المقدار مختلفتين في النوع
يتم حساب المجال الناتج عن كل شحنة ويتم الجمع الاتجاهي حسب قواعد المتجهات
مثال محلول
حساب المجال الناتج عن ثنائي القطب على امتداد المحور للثنائي عند نقطة تبعد عن مركز الثنائي
(X) مسافة قدرها
النقطة خاضعة لمجالين من الشحنة الموجبة
\[E_1=\frac{1}{4𝜋ع_0}\frac{q}{(X-\frac{1}{2}d)^2}\] والاتجاه نحو اليمين
من الشحنة السالبة
\[E_2=\frac{1}{4𝜋ع_0}\frac{q}{(X+\frac{1}{2}d)^2}\] والاتجاه نحو اليسار
فتكون المحصلة\[E_{net}=E_1-E_2\]
\[E_1>E_2\]
\[E_{net}=\frac{1}{4𝜋ع_0}\frac{q}{(X-\frac{1}{2}d)^2}-\frac{1}{4𝜋ع_0}\frac{q}{(X+\frac{1}{2}d)^2}\]
والاتجاه نحو اليمين
بإخراج العامل المشترك\[\frac{q}{4𝜋ع_0X^2}\]
تصبح العلاقة \[E_{net}=\frac{q}{4𝜋ع_0X^2}[\frac{1}{(1-\frac{d}{2X})^2}-\frac{1}{(1+\frac{d}{2X})^2}]\] بتوحيد المقامات \[E_{net}=\frac{q}{4𝜋ع_0X^2}[\frac{(1+\frac{d}{2X})^2-(1-\frac{d}{2X})^2}{(1-\frac{d}{2X})^2(1+\frac{d}{2X})^2}]\]
\[E_{net}=\frac{q}{4𝜋ع_0X^2}[\frac{(1+\frac{d}{X}+\frac{d^2}{4X^2})-(1-\frac{d}{X}+\frac{d^2}{4X^2})}{(1-\frac{d}{2X})^2(1+\frac{d}{2X})^2}]\]
\[E_{net}=\frac{q}{4𝜋ع_0X^2}[\frac{(1+\frac{d}{X}+\frac{d^2}{4X^2}-1+\frac{d}{X}-\frac{d^2}{4X^2})}{(1-\frac{d}{2X})^2(1+\frac{d}{2X})^2}]\]
X>>d إذا كان
\[\frac{d}{2X}=0.0\]\[E_{net}=\frac{2dq}{4𝜋ع_0X^3}=\frac{dq}{2𝜋ع_0X^3}=\frac{2kdq}{X^3}\]
\[P=q.d\]يدعى عزم ثنائي القطب وهو كمية متجهه واتجاهه من الشحنة السالبة إلى الموجبة عكس المجال الكهربائي
مثال محلول
حساب المجال الناتج عن ثنائي القطب عند نقطة تقع على العمود المنصف و تبعد عن مركز الثنائي
(y) مسافة قدرها
النقطة خاضعة لمجالين \[E_1,E_2\] عند تحليل المجال الناتج عن كل شحنة الى مركبتين نلاحظ من خلال التناظر
\[𝐸_{1y} = {𝐸_2y}\]المحصلة لهما تساوي الصفر
من خلال الشكل \[r=\sqrt{(\frac{d}{2})^2+y^2}, Cos 𝜃= \frac{\frac{d}{2}}{r}\]
\[E_{1X}=E_1. Cos 𝜃=\frac{k.q}{r^2}.\frac{\frac{d}{2}}{r}=\frac{k.q}{(\frac{d}{2})^2+y^2}.\frac{\frac{d}{2}}{\sqrt{(\frac{d}{2})^2+y^2}}\]
\[𝐸_{1x} =\frac{kqd}{2[{(\frac{d}{2})^2+y^2}]^{3/2}}\]
\[E_{2X}=E_2. Cos 𝜃=\frac{k.q}{r^2}.\frac{\frac{d}{2}}{r}=\frac{k.q}{(\frac{d}{2})^2+y^2}.\frac{\frac{d}{2}}{\sqrt{(\frac{d}{2})^2+y^2}}\]
\[𝐸_{2x} =\frac{kqd}{2[{(\frac{d}{2})^2+y^2}]^{3/2}}\]
\[E_{net}=𝐸_{1x}+𝐸_{2x}=\frac{kqd}{2[{(\frac{d}{2})^2+y^2}]^{3/2}}+\frac{kqd}{2[{(\frac{d}{2})^2+y^2}]^{3/2}}\]
\[E_{net}= -\frac{kqd}{[{(\frac{d}{2})^2+y^2}]^{3/2}}\]
الإشارة السالبة تعني باتجاه المجور الأفقي السالب
(y>> d) اذا كانت
\[\frac{d}{2}≈
0\]
\[E_{net}= -\frac{kqd}{x^3} \]
التوزيعات العامة للشحنات
إذا كان لدينا عدد كبير جدا من الشحنات وطلب حساب المجال الناتج عنها لا يمكن إيجاد المحصلة
بالطريقة السابقة نستخدم التكامل لإيجاد المحصلة بشرط الشحنات موزعة بشكل منتظم
نأخذ جزء صغير من شحنة الجسم
\[dq\]
ونحسب مجالها ثم نجري التكامل على كامل الجسم
هناك مشكلة إذا كانت الشحنة موزعة على طول جسم أو سطح جسم او على حجم جسم
على طول خط
\[𝑑𝑞=λ𝑑𝑥\]
على مساحة سطح
\[𝑑𝑞=𝛿𝑑A\]
على حجم جسم
\[𝑑𝑞=𝜌𝑑V\]
( اثرائي ) مثال محلول
سلك طولة محدود ومشحون بشكل منتظم كما في الشكل أدناه
أحسب مقدار واتجاه المجال عند نقطة تقع على امتداد الخط المقام
من منتصف السلك
نأخذ شحنة صغيرة
\[dq\]ونحسب مجالها ثم نجري التكامل
على كامل السلك
لو أخذنا نصف السلك ومن خلال التناظر نلاحظ مع
النصف الاخر
\[E_1X=E_2X\]
وتعاكسها في الاتجاه اذا محصلتها صفر
أما المركبة الرأسية للمجال والناتج من كل طرف من السلك فهما متساويان في المقدار وبنفس الاتجاه
\[ d𝐸_1Y =d 𝐸_1 Cos 𝜃 , d𝐸_2Y =d 𝐸_2 Cos 𝜃\]
لذلك لحساب قيمه المجال نحسب مقدار لنصف طول السلك ونضاعف القيمة فنحصل على قيمة المجال
.
من الشكل \[r=\sqrt{X^2+Y^2}, Cos 𝜃= \frac{Y}{r}\]
\[E=2\int_{{\,0}}^{{\,a}}{dE_Y}=2\int_{{\,0}}^{{\,a}}{k\frac{dq}{r^2}Cos 𝜃}=2k\int_{{\,0}}^{{\,a}}{\frac{λ𝑑𝑥}{r^2}\frac{Y}{r}}\]
\[E=2kλY\int_{{\,0}}^{{\,a}}{\frac{{𝑑𝑥}}{({X^2+Y^2})^{3/2}}}\]
والتكامل يتم إنجازه بوساطة الجداول
\[\int_{{\,0}}^{{\,a}}{\frac{{𝑑𝑥}}{({X^2+Y^2})^{3/2}}}=|\frac{1}{Y^2}\frac{X}{\sqrt{X^2+Y^2}}|_{{\,0}}^{{\,a}}=\frac{1}{Y^2}\frac{a}{\sqrt{a^2+Y^2}}\]
\[E=2kλY\frac{1}{Y^2}\frac{a}{\sqrt{a^2+Y^2}}\]
فيكون قيمة المجال الناتج عن سلك طولة محدود
\[E=2kλ\frac{1}{Y}\frac{a}{\sqrt{a^2+Y^2}}\] هي طول نصف السلك : a
إذا كان السلك طوله لانهائي فإن a→∞\[\frac{a}{\sqrt{a^2+Y^2}}→1\]
\[E=\frac{2kλ}{y}\]
القوة الناتجة عن المجال الكهربائي
إذا تم وضع شحنة داخل مجال كهربائي
فإن الجسيم سوف يتأثر بقوة كهربائية
\[\vec F_e=q.\vec E\]
إذا كانت الشحنة الموضوعة داخل المجال موجبة فإنها سوف تتحرك بإتجاه المجال وإذا كانت الشحنة سالبة فإنها سوف تتحرك عكس المجال
التجربة التالية توضح القوة الكهربائية المؤثرة على شحنة إختبار وضعت داخل مجال كهربائي
وحركة شحنة الاختبار عند وضعها داخل مجال كهربائي اضغط على ايقونة التشغيل وشاهد اتجاه الحركة وهو نفسه اتجاه القوة ويمكن ان تغير نوع الشحنه المولدة للمجال ومقدارها
وبالامكان تحديد اتجاه المجال بالضغط على ايقونة المجال
حدد اتجاه ومقدار القوة المؤثرة على إلكترون وضع داخل مجال في الحالات التالية
اضغط هنا تظهر طريقة الحل
اضغط هنا تظهر طريقة الحل
اضغط هنا تظهر طريقة الحل
اضغط هنا تظهر طريقة الحل
(اثرائي ) ثنائي القطب في مجال كهربائي
r=d وهي البعد بين القطبين
F=q.E القوة المؤثرة على أحد القطبين
𝜃 هي الزاوية بين الذراع والقوة
فنحصل على العلاقة
\[ 𝜏 = q.d. E . Sin 𝜃 \]
\[ 𝜏 = p. E . Sin 𝜃 \]
No comments:
Post a Comment