الموجات الموقوفة |
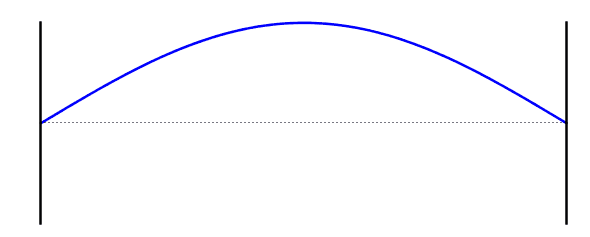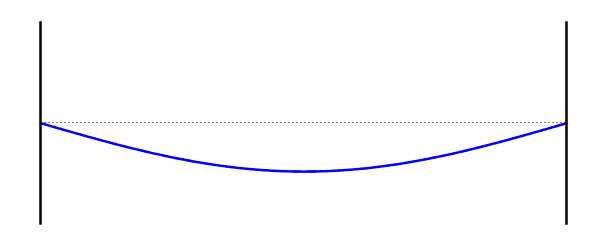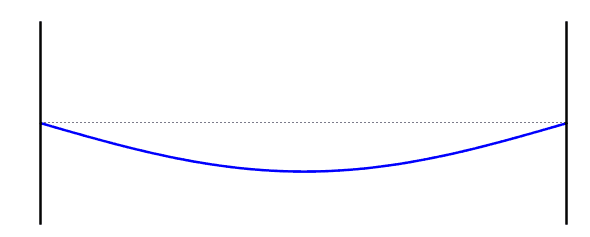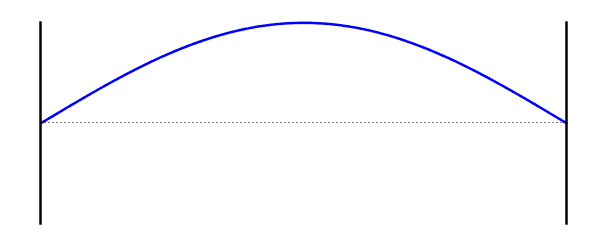
التردد الأساسي (الموجة الواقفة الاولى)
هناك العديد من أوضاع الاهتزاز الأخرى لسلسلة مثبتة في كل طرف. كل وضع يسمى متوافقة. عند التوافقي الثاني ، تتكون الموجة الواقفة من جزأين. الطول الموجي هو نصف الطول الموجي الأساسي ، وبالتالي فإن التردد هو ضعف التردد الموجي الأساسي.
الموجة التوافقية الثانية
\[f = 2f_0\] \[L = λ\] \[ λ = L \]
عند التوافقية الثالثه ، تتكون الموجة الواقفة من ثلاثة أجزاء. الطول الموجي يساوي ثلث الطول الموجي الأساسي ، وبالتالي فإن التردد يساوي ثلاثة أضعاف التردد الموجي الأساسي.
الموجة التوافقية الثالثة
\[f = 3f_0\] \[L = \frac{3λ}{2}\] \[λ = \frac{2L}{3}\]
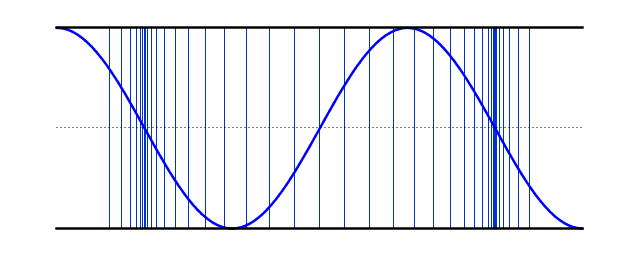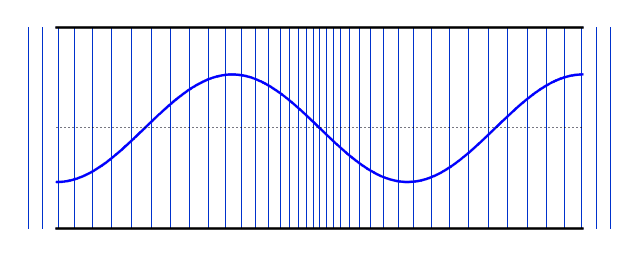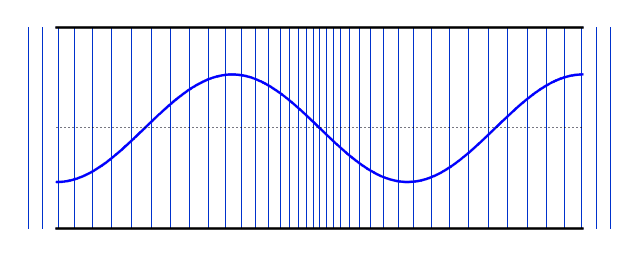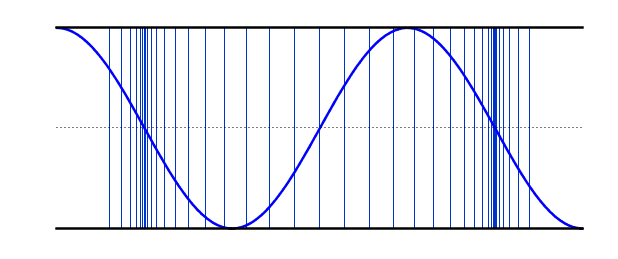
عندما تنتقل الموجة الصوتية إلى أسفل أنبوب مملوء بالهواء ، فإن بعض الموجات الصوتية ستنعكس مرة أخرى عندما تصل إلى نهاية الأنبوب ، سواء كان طرف الأنبوب مفتوحًا أم مغلقًا. سوف تنعكس الموجات الصوتية ذهابًا وإيابًا من طرف إلى آخر. ستشكل بعض الترددات الاهتزازية المحددة موجات ثابتة في عمود الهواء ، وهذه هي الترددات التي يتردد صداها في عمود الهواء. تستخدم العديد من الآلات الموسيقية الموجات الواقفة في أعمدة الهواء كمصدر أولي لموجاتها الصوتية. تستخدم آلات النفخ النحاسية والخشبية أعمدة الهواء لإنتاج أصواتها المميزة.
عندما تتشكل موجة واقفة في عمود هوائي ، يوجد دائمًا بطن في أي طرف مفتوح وعقدة \ في أي طرف مغلق. ملاحظة: العقد والبطن هي النقاط التي تخضع للحد الأدنى والحد الأقصى من الإزاحة على التوالي. من حيث الضغط ، هم في الواقع عكس ذلك. العقد هي عقد ضغط والبطن هي انخفاض ضغط. يمكن ملاحظة ذلك في الموجات الطولية في الرسوم المتحركة - لاحظ كيف أن المناطق التي توجد بها خطوط ثابتة (عُقد ) بها اختلافات كبيرة في كثافة الخط في (البطن ). عند استخدام كلمة عقدة أو بطن في انبوب الهواء مفتوحًا عند كلا الطرفين ، فإن الوضع الأساسي للاهتزاز يحتوي على عقدة واحدة في المركز وبطن في كل نهاية. يُعرف هذا أيضًا باسم التوافقي الأول
التوافقي الأول : يكون طول عمود الهواء مساويًا لنصف الطول الموجي للموجة الواقفة ، لأن المسافة من بطن إلى أقرب عقدة تالية هي ربع طول موجي و ربعين متتالين نصف طول موجة . يُعرف تردد التوافقي الأول باسم التردد الأساسي في الرسوم البيانية أدناه ، تظهر الموجة الواقفة في كل من الموجة الطولية والأشكال المستعرضة. الموجة الصوتية الفعلية طولية ، لكن من الأسهل تصور العقد والعقد في شكل موجة عرضية مكافئة..
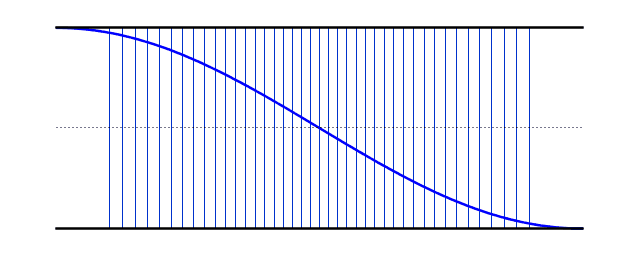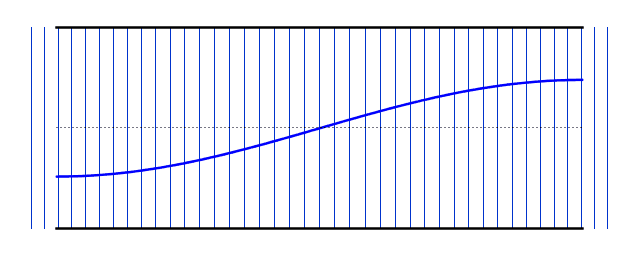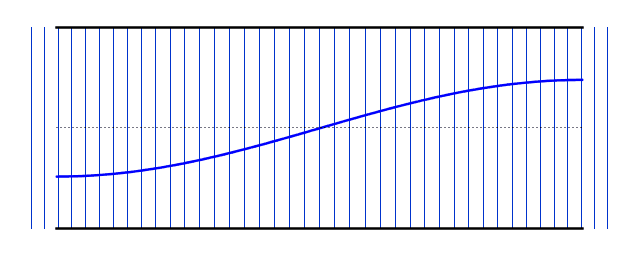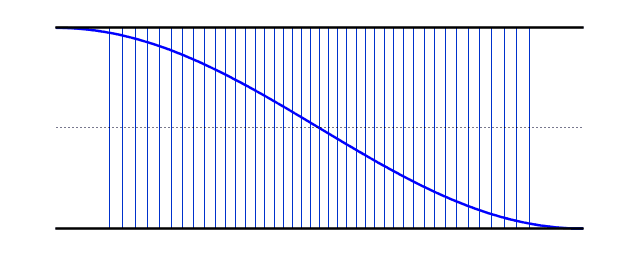
(التوافقية الأولى)
عند التوافقي الثاني ، يكون الطول الموجي هو نصف الطول الموجي الأساسي ، وبالتالي يكون التردد ضعف الطول الموجي الأساسي.
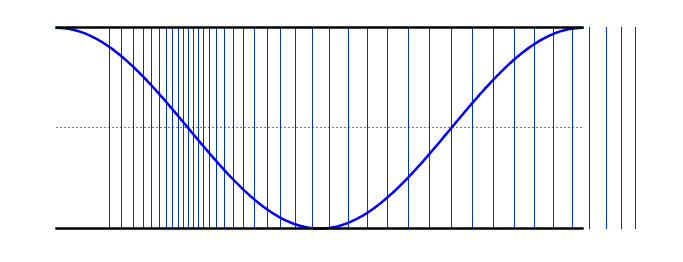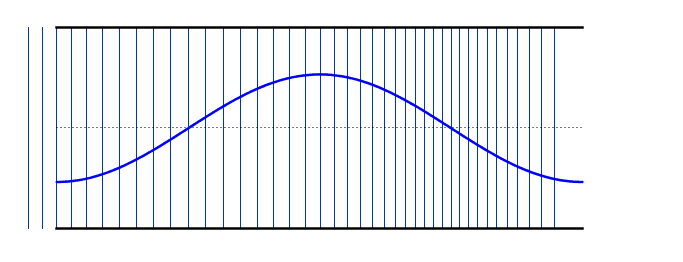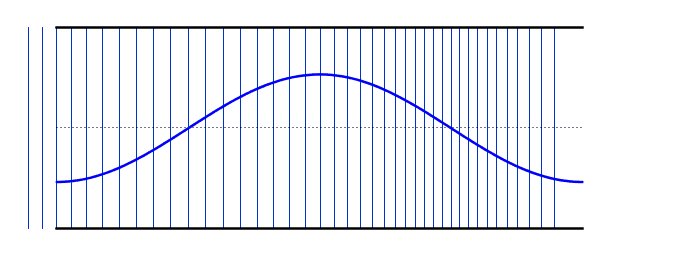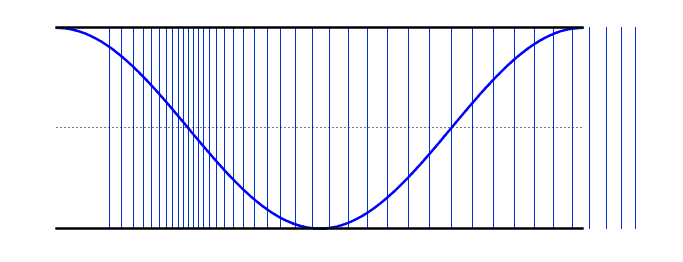
التوافقية الثانية
عند التوافقي الثالث ، يكون الطول الموجي ثلث الطول الموجي الأساسي ، وبالتالي يكون التردد ثلاثة أضعاف الطول الموجي الأساسي.
التوافقية الثالثة
عندما تتشكل موجة واقفة في عمود هوائي ، يوجد دائمًا بطن في أي طرف مفتوح وعقدة في أي طرف مغلق.
إذا كان عمود الهواء مفتوحًا من أحد الطرفين ومغلقًا من الطرف الآخر ، فإن الوضع الأساسي للاهتزاز يكون له بطن في الطرف المفتوح وعقدة في النهاية المغلقة. يُعرف هذا أيضًا باسم التوافقي الأول . .
For التوافقي الأول ، طول عمود الهواء يساوي ربع الطول الموجي للموجة الواقفة ، لأن المسافة من عقدة إلى أقرب نقطة بطن هي ربع طول الموجة.
يُطلق على تردد التوافقي الأول التردد الأساسي (f0).
في المخططات أدناه ، تظهر الموجة الواقفة في شكليها الطولي والعرضي. الموجة الصوتية الفعلية طولية ، ولكن من السهل تصور العقد والبطون في شكل موجة عرضية مكافئة.
(التوافقية الأولى)
\[f = f_0\]\[ L = \frac{λ}{4}\] \[λ = 4L\]
عند التوافقي الثالث ، تتكون الموجة الواقفة من جزء ونصف "مقاطع". الطول الموجي يساوي ثلث الطول الموجي الأساسي ، وبالتالي فإن التردد يساوي ثلاثة أضعاف التردد الموجي الأساسي. بالنسبة إلى أعمدة الهواء ذات النهاية المغلقة ، لا يوجد توافقية ثانية. لأن الوضع الثاني يبلغ ثلاثة أضعاف تردد الأساسي ، فهو في الواقع التوافقي الثالث.
يمكن للأعمدة الهوائية المغلقة عند أحد الأطراف أن تشكل موجات واقفة عند التوافقيات الفردية.
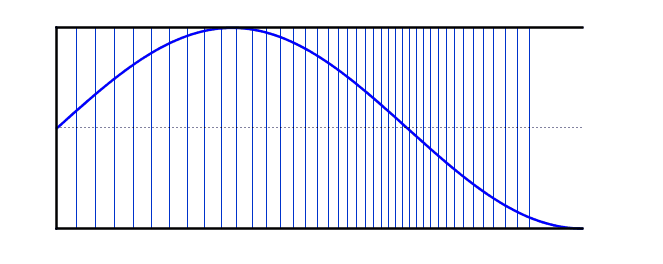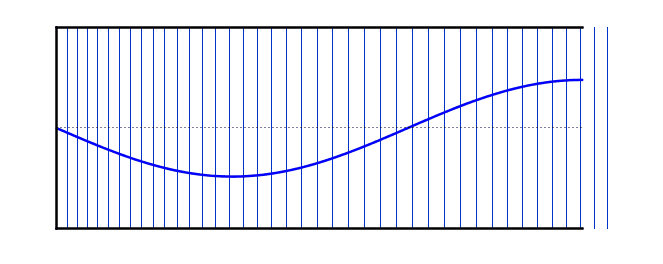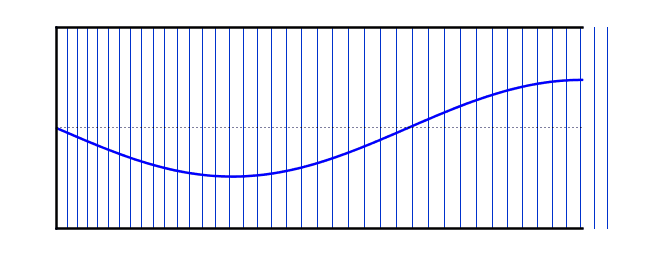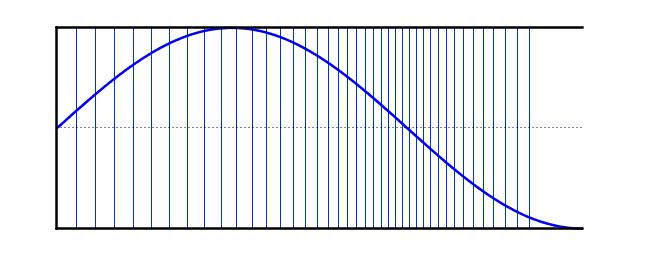
التوافقية الثالثة >
\[f = 3f_0\]\[ L =\frac{ 3λ}{4}\]\[λ=\frac{ 4L}{3}\]
عند التوافقي الخامس ، تتكون الموجة الدائمة من موجة وربع . الطول الموجي يساوي خمس أضغااف الطول الموجي للموجة الأساسية ، وبالتالي فإن التردد يساوي خمسة أضعاف التردد الموجي الأساسي
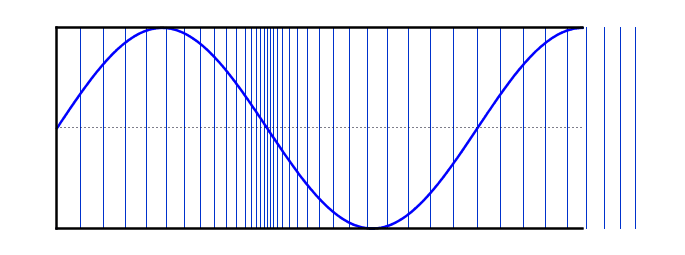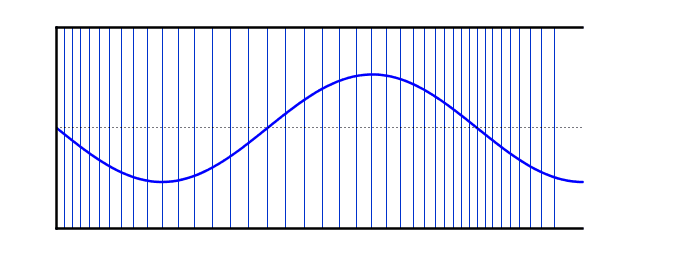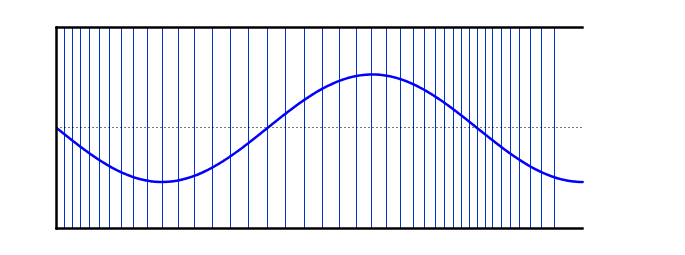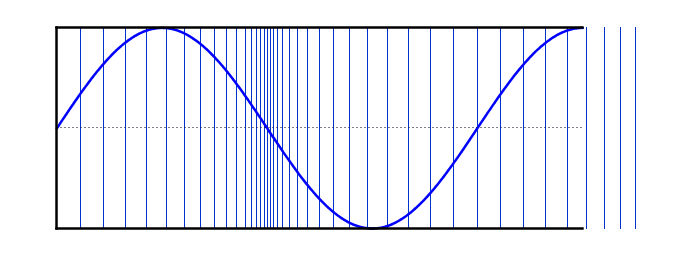
التوافقية الخامسة
\[f = 5f_0\] \[L =\frac{ 5λ}{4}\]\[λ = \frac{4L}{5}\]
فيما يلي محاكاة واحدة حيث يمكن مقارنة موجات واقفة مختلفة على الأوتار وأعمدة الهواء:
Comments
Post a Comment