📄 اطبع pdf
00971504825082

<<<حركة جسم على مستوى أفقي >>>

معادلات الحركة على مستوى أفقي أملس

الحالة 1: قوة شد أفقية

محصلة القوى على المحور الأفقي \[ΣF_x = T = m · a →\] محصلة القوى على المحور االرأسي \[ΣF_y = N - mg = 0 \] التسارع \[ a = \frac {T}{m}\] السرعة \[v_f = v_0+ a·t\] الإزاحة \[ Δx = v_0·t + ½a·t²\]

القوة العمودية (N):

\[ ΣF_y = N - m·g = 0 →\] \[ N = m·g\]

الحالة 2: قوة شد مائلة بزاوية θ

محصلة القوى على المحور الأفقي \[ ΣT_x = T·cosθ = m·a → \] محصلة القوى على المحور االرأسي \[ ΣFy = N + T·sinθ - m·g = 0\] التسارع \[a = \frac {T·cosθ}{m}\] السرعة \[v_f = v_0 + a·t\] الإزاحة \[ Δx = v_0·t + ½a·t²\]

القوة العمودية (N):

\[ ΣFy = N + T·sinθ - m·g = 0 →\] \[ N = m·g - F·sinθ\]

رموز المتغيرات:

• T: قوة الشد (N)
• m: كتلة الجسم (kg)
• a: التسارع (m/s²)
• v₀: السرعة الابتدائية (m/s)
• t: الزمن (s)
• θ: زاوية ميلان القوة (بالدرجات)
• g: تسارع الجاذبية (9.8 m/s²)

تحليل حركة جسم على سطح أفقي خشن

ملاحظات:
- μ_s: معامل الاحتكاك الساكن
\[μ_S=\frac {F_S}{N}→F_S=μ_S*N\] - μ_k: معامل الاحتكاك الحركي
\[μ_K=\frac {F_K}{N}→F_K=μ_K*N\] - يجب استخدام الوحدات المتوافقة (نيوتن، كجم، م/ث²)

أولاً: قوة الشد أفقية

القوة العمودية (N) = كتلة الجسم (m) × تسارع الجاذبية (g)
N = m × g

شرط الحركة:

الجسم يتحرك إذا كانت → \[ T > μ_s × N \] الجسم لا يتحرك إذا كانت → \[T ≤ μ_s × N \]

في حالة الحركة:

محصلة القوى على المحور الأفقي \[ΣF_x = T - f_K =T - μ_k × N= ma \] محصلة القوى على المحور االرأسي \[ ΣFy = N - m·g = 0\] التسارع \[(a) = \frac {T - μ_k × N}{ m}\] السرعة \[v_f = v_0 + a·t\] الإزاحة \[ Δx = v_0·t + ½a·t²\]

ثانياً: قوة الشد مائلة بزاوية

\[θ\]

المركبة الأفقية \[T_x = T × cosθ\] المركبة العمودية \[T_y = T × sinθ\]

إذا كانت قوة الشد تميل للأعلى فإن القوة العمودية \[(N) = m × g - T_y\] إذا كانت قوة الشد تميل للأسفل فإن القوة العمودية \[(N) = m × g + T_y\]

شرط الحركة:

الجسم يتحرك إذا كانت → \[ T_X > μ_s × N \] الجسم لا يتحرك إذا كانت → \[T_X ≤ μ_s × N \]

في حالة الحركة:

قوة الشد تميل للأعلى فإن محصلة القوى على المحور الأفقي \[ΣF_x = T_x - f_K =T_x - μ_k × N=T_x - μ_k × ( m × g - T_y)= ma \] محصلة القوى على المحور االرأسي \[ ΣFy = N +T_y - m·g = 0\] التسارع \[a =\frac { T_x - μ_k ×( m × g - T_y)}{ m}\] السرعة \[v_f = v_0 + a·t\] الإزاحة \[ Δx = v_0·t + ½a·t²\]
قوة الشد تميل للأسفل فإن محصلة القوى على المحور الأفقي \[ΣF_x = T_x - f_K =T_x - μ_k × N=T_x - μ_k × ( m × g + T_y)= ma \] محصلة القوى على المحور االرأسي \[ ΣFy = N -T_y - m·g = 0\] التسارع \[a =\frac { T_x -μ_k × ( m × g + T_y)}{ m}\] السرعة \[v_f = v_0 + a·t\] الإزاحة \[ Δx = v_0·t + ½a·t²\]

محاكاة سحب صندوق على مستوى أفقي

كتلة الصندوق (كجم): القوة المطبقة (نيوتن): معامل الاحتكاك: ابدأ المحاكاة

 
الجملة المادية تتحرك بنفس التسارع لأن الخيط لا يمتط وقوة الشد متساوية على طرفي الخيط عند دراسة الجسم نحدد نحدد القوى المؤثرة على الجسم ونطبق قانون نيوتن الثاني على الجسم حتى نحصل على تسارع الجملة

تحليل قوى السحب مع الاحتكاك

الحالة	المعادلات	شرط الحركة	تطبيق عملي
قوة شد أفقية (جسم ساكن)	Fs,max = μsN ΣFx = T - Fs = 0	T ≤ μsmg	سحب خزانة ثقيلة
قوة شد أفقية (جسم متحرك)	Fk = μkN ΣFx = T - Fk = ma	T > μsmg	جر عربة على أرضية
قوة شد مائلة (θ مع الأفقي)	Tx = Tcosθ Ty = Tsinθ N = mg - Ty	Tx > μs(mg - Ty)	سحب صندوق بحبل مائل

القيم النموذجية لمعامل الإحتكاك

المقدار	الرمز	قيم نموذجية	وحدة القياس
الكتلة	m	10 - 100	كجم
معامل الاحتكاك السكوني	μs	0.3 (خشب-خشب) 0.6 (مطاط-أسفلت)	بدون وحدة
معامل الاحتكاك الحركي	μk	0.2 (خشب-خشب) 0.4 (مطاط-أسفلت)	بدون وحدة
قوة الشد	T	50 - 500	نيوتن

تفسيرات فيزيائية:

• الاحتكاك السكوني: يمنع الحركة الأولية حتى الوصول للقوة الحرجة
• الاحتكاك الحركي: يقاوم الحركة بعد بدئها بقيمة ثابتة تقريبًا
• القوة العمودية (N): تتأثر بالمكون الرأسي للشد في الحالات المائلة

تطبيقات عملية:

1. تصميم أنظمة الفرامل في السيارات
2. حساب القوة اللازمة لسحب الأثاث
3. تحسين أداء الإطارات على الطرق
4. تصميم أنظمة النقل بالسيور

اكتب تعليقا واذا كان هناك خطأ اكتبه وحدد مكانه Write a comment, and if there is mistake, write and specify its location

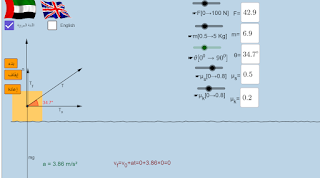
No comments:

Post a Comment