اسئلة مراجعة الفصل الأول فيزياء11 متقدم حسب الهيكل( 2024-2025) Review questions for the first semester, 11A Physics

 

📄 اطبع pdf
00971504825082

<<< اسئلة مراجعة الفصل الأول فيزياء 11 متقدم حسب الهيكل( 2024-2025) >>>

رَبِّ أَوْزِعْنِي أَنْ أَشْكُرَ نِعْمَتَكَ الَّتِي أَنْعَمْتَ عَلَيَّ وَعَلَى وَالِدَيَّ وَأَنْ أَعْمَلَ صَالِحًا تَرْضَاهُ وَأَصْلِحْ لِي فِي ذُرِّيَّتِي إِنِّي تُبْتُ إِلَيْكَ وَإِنِّي مِنَ الْمُسْلِمِينَ .

رَبَّنَا هَبْ لَنَا مِنْ أَزْوَاجِنَا وَذُرِّيَّاتِنَا قُرَّةَ أَعْيُنٍ وَاجْعَلْنَا لِلْمُتَّقِينَ إِمَامًا

رَبِّ هَبْ لِي حُكْمًا وَأَلْحِقْنِي بِالصَّالِحِينَ واجْعَل لِّي لِسَانَ صِدْقٍ فِي الآخِرِينَ وَاجْعَلْنِي مِن وَرَثَةِ جَنَّةِ النَّعِيمِ

1

أحد المعادلات التالية تعبر عن تعبر عن موقع المتجه $$\vec A$$ في الشكل أدناه

$$\overrightarrow A = -2 \widehat X ,+ 3 \widehat Y ,- 2\widehat Z -C$$	$$\overrightarrow A = +2 \widehat X, - 3 \widehat Y,+ 2\widehat Z -A$$
$$\overrightarrow A = +2 \widehat X, + 3 \widehat Y, - 2\widehat Z -D$$	$$\overrightarrow A = -2 \widehat X ,+ 3 \widehat Y, + 2\widehat Z -B$$

اضغط هنا تظهر طريقة الحل

أختر الإجابة الصحيحة

---

A

---

B

---

C

---

D

---

2

(A) المتجه
إحداثياته الديكارتية $$\overrightarrow A =( +23 \widehat X , +59 \widehat Y )$$ أحسب مقدار واتجاه المتجه

A=63.3 , 𝜃 =68.7 0 -C	A=86.5 , 𝜃 =35.8 0 -A
A=86.5 , 𝜃 =35.8 0 -D	A=63.3 , 𝜃 =45.90 -B

اضغط هنا تظهر طريقة الحل

أختر الإجابة الصحيحة

---

A

---

B

---

C

---

D

---

3

متجه احداثياته الديكارتي $$\overrightarrow A = (-3 \widehat X ,-5 \widehat Y)$$ فإنه يصنع زاوية مع محور $$X$$ الموجب بدوران عكس عقارب الساعة

$$𝜃=239^0\;\;\;\;\;\;-C$$	$$𝜃=59^0\;\;\;\;\;\;-A$$
$$𝜃=121^0;\;\;\;\;\;-D$$	$$𝜃=31^0\;\;\;\;\;\;-B$$

اضغط هنا تظهر طريقة الحل

أختر الإجابة الصحيحة

---

A

---

B

---

C

---

D

---

4

اثرت قوتين على جسم مركبات كل قوة موضحه في الشكل أدناه فإن محصلة القوتين واتجاه المحصلة تعادل $$\vec F_{net}=\vec F_1+\vec F_2$$

F(net)=10.8 N , 𝜃=38.8 0 -C	F(net)=6.3 N , 𝜃=54.2 0 -A
F(net)=9.5 N , 𝜃=71.6 0 -D	F(net)=8.4 N , 𝜃=28.4 0 -B

اضغط هنا تظهر طريقة الحل

أختر الإجابة الصحيحة

---

A

---

B

---

C

---

D

---

5

قياس الزاوية المحصورة بين المتجهين التالين $$\overrightarrow A = \widehat X + 2 \widehat Y + 3\widehat Z \;\;\;\;\;\; \overrightarrow B = -2 \widehat X +2 \widehat Y + 2 \widehat Z \nonumber$$ يعادل

𝜃=310 -C	𝜃=670 -A
𝜃=260 -D	𝜃=540 -B

اضغط هنا تظهر طريقة الحل

أختر الإجابة الصحيحة

---

A

---

B

---

C

---

D

---

6

في الشكل أدناه المتجهان $$\overrightarrow A =( +5 \widehat X , +4 \widehat Y ) \;\;\;\;\;\; \overrightarrow B =( -4 \widehat X ,+2 \widehat Y ) \nonumber$$
أوجد مقدار $$C=\vec A . \vec B=.......$$

$$A.B=-12 \;\;\;\;\;\;-C$$	$$A.B=12 \;\;\;\;\;\;-A$$
$$A.B=-28\;\;\;\;\;\;-D$$	$$A.B=28\;\;\;\;\;\;-B$$

اضغط هنا تظهر طريقة الحل

أختر الإجابة الصحيحة

---

A

---

B

---

C

---

D

---

7

$$\overrightarrow A = +2 \widehat X + 3 \widehat Y - 2\widehat Z \;\;\;\;\;\; \overrightarrow B = -3 \widehat X +2 \widehat Y + 2 \widehat Z \nonumber$$ ( C ) أوجد مقدار $$|\vec C|= |2\vec A+3\vec B|$$

C= 18.1 -C	C=10.5 -A
C=16.3 -D	C=12.8 -B

اضغط هنا تظهر طريقة الحل

أختر الإجابة الصحيحة

---

A

---

B

---

C

---

D

---

8

احسب السرعة المتجهة المتوسطة اذا تحرك أحمد حسب المخطط التالي $$A\Rightarrow B\Rightarrow C \Rightarrow D$$ خلال زمن قدره $$t=3\;\;min$$

$$\vec v= 1.25\;\;m/s \;\;\;\;\;\;\;-C$$	$$\vec v= 0.78\;\;m/s \;\;\;\;\;\;\; -A$$
$$\vec v= 2.35\;\;m/s \;\;\;\;\;\;\; -D$$	$$\vec v= 0.25\;\;m/s \;\;\;\;\;\;\; -B$$

اضغط هنا تظهر طريقة الحل

أختر الإجابة الصحيحة

---

A

---

B

---

C

---

D

---

9

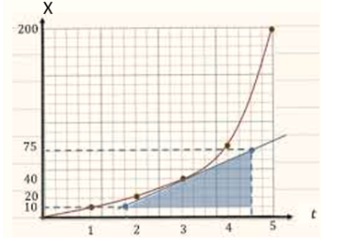
تم رسم العلاقة بين الموقع والزمن لدراجة فإن سرعة الدراجة خلال كامل الفترة تعادل

$$\bar v=2.12\;m/s \;\;\;\;\;\; -C$$	$$\bar v=0.44\;m/s \;\;\;\;\;\; -A$$
$$\bar v=1.28\;m/s \;\;\;\;\;\; -D$$	$$\bar v=3.62\;m/s \;\;\;\;\;\; -B$$

اضغط هنا تظهر طريقة الحل

أختر الإجابة الصحيحة

---

A

---

B

---

C

---

D

---

10

ميل المماس للمنحنى البياني الموقع والزمن يعادل

التسارع المتوسط -C	السرعة اللحظية -A
التسارع اللحظي -D	السرعة المتوسطة -B

اضغط هنا تظهر طريقة الحل

أختر الإجابة الصحيحة

---

A

---

B

---

C

---

D

---

11

الخط البياني يبين العلاقة بين السرعة والزمن لدراجة تتحرك في بعد واحد

أفضل خط بياني يبين العلاقة بين التسارع والزمن لهذه الحركة

اضغط هنا تظهر طريقة الحل

أختر الإجابة الصحيحة

---

A

---

B

---

C

---

D

---

12

يصف الخط البياني موقع جسم ما يتحرك في بعد واحد
كدالة للزمن في أي فترة زمنية يصل الجسم إلى أقصى سرعة

$$t=5 \;s\Rightarrow t=7\;s\;\;\;\;\;\; -C$$	$$t=0\; s\Rightarrow t=3\;s\;\;\;\;\;\; -A$$
$$t=7\; s\Rightarrow t=10\;s\;\;\;\;\;\; -D$$	$$t=3\; s\Rightarrow t=5\;s\;\;\;\;\;\; -B$$

اضغط هنا تظهر طريقة الحل

أختر الإجابة الصحيحة

---

A

---

B

---

C

---

D

---

13

اسقط حجر راسيا إلى الأسفل من سطح برج وبسرعة ابتدائية مقدارها $$v=6\;\;m/s$$ فوصل الحجر إلى الأرض بعد زمن قدره $$t=5\;\; s$$ بإهمال مقاومة الهواء فإن ارتفاع المبنى يعادل اعتبر $$g=9.81 \;m/s^2$$

$$ℎ=95.8 \;𝑚\;\;\;\;\;\;-C$$	$$ℎ=181.5 \;𝑚\;\;\;\;\;\;-A$$
$$ℎ=152.6 \;𝑚\;\;\;\;\;\;-D$$	$$ℎ=109.4 \;𝑚\;\;\;\;\;\;\;\;\;\;\;\;-B$$

اضغط هنا تظهر طريقة الحل

أختر الإجابة الصحيحة

---

A

---

B

---

C

---

D

---

14

تم قذف كرة راسيا إلى أعلى وعادت إلى الأرض بإهمال مقاومة الهواء أحد الخطوط البيانية تبين العلاقة بين السرعة والزمن لحركة الجسم

اضغط هنا تظهر طريقة الحل

أختر الإجابة الصحيحة

---

A

---

B

---

C

---

D

---

15

الخط البياني التالي يبين العلاقة بين التسارع والزمن لحركة سيارة سباق التي بدأت في اللحظة صفر بسرعة ابتدائية مقدارها $$v=4\;\;m/s$$ رتب سرعة السيارات النهائية لكل مرحلة من مراحل السباق من الأدنى إلى الأعلى

$$v_{f1} \Rightarrow v_{f3}\Rightarrow v_{f4}\Rightarrow v_{f2}\;\;\;\;\;\; -C$$	$$v_{f1} \Rightarrow v_{f4}\Rightarrow v_{f2}= v_{f3}\;\;\;\;\;\; -A$$
$$v_{f4} \Rightarrow v_{f3}\Rightarrow v_{f1}\Rightarrow v_{f2}\;\;\;\;\;\; -D$$	$$v_{f3} \Rightarrow v_{f4}\Rightarrow v_{f1}= v_{f2}\;\;\;\;\;\; -B$$

اضغط هنا تظهر طريقة الحل

أختر الإجابة الصحيحة

---

A

---

B

---

C

---

D

---

16

معادلة الموقع لجسم بدلالة الزمن $$X(t)=3-6.t-10.t^2+2.t^3$$ فإن تسارع الجسم في اللحظة $$t=3\;\;s$$ تعادل

$$a=12 \;m/s^2\;\;\;\;\;\;-C$$	$$a=18 \;m/s^2\;\;\;\;\;\;-A$$
$$a=14\;m/s^2\;\;\;\;\;\;-D$$	$$a=16 \;m/s^2\;\;\;\;\;\;-B$$

اضغط هنا تظهر طريقة الحل

أختر الإجابة الصحيحة

---

A

---

B

---

C

---

D

---

17

المعادلة التالية تبين العلاقة بين التسارع والزمن لحركة جسم في بعد واحد في بداية الحركة السرعة والموضع يساويان صفرًا $$𝑎_𝑡=4𝑡−3$$ فإن المسافة المقطوعة بعد زمن قدره $$t=8{s}$$ تعادل

$$X=196.2 \;𝑚\;\;\;\;\;\;-C$$	$$X=322.8 \;𝑚\;\;\;\;\;\;-A$$
$$X=136.5 \;𝑚\;\;\;\;\;\;-D$$	$$X=245.3 \;𝑚\;\;\;\;\;\;-B$$

اضغط هنا تظهر طريقة الحل

أختر الإجابة الصحيحة

---

A

---

B

---

C

---

D

---

18

في سباق القوارب أراد قارب أن يقطع مسافة 1200 متر شرقا في نهريحري نحو الغرب بسرعة حريان $$v=\;5m/s$$ نحو الغرب في حين كانت سرعة القارب بالنسبة للنهر $$v=\;25m/s$$ نحو الشرق فإن الزمن اللازم لقطع هذه المسافة تعادل

$$t=240 \;s\;\;\;\;\;\;-C$$	$$t=48 \;s\;\;\;\;\;\;-A$$
$$t=60 \;s\;\;\;\;\;\;-D$$	$$t=40 \;s\;\;\;\;\;\;-B$$

اضغط هنا تظهر طريقة الحل

أختر الإجابة الصحيحة

---

A

---

B

---

C

---

D

---

19

قذف مدفع قذيفة بسرعة أفقية ابتدائية $$v_0=31 \;\;m/s$$ من سطح مبنى فوصلت القذيفة إلى الأرض بعد زمن قدره $$t=4\;\;s$$ فإن سرعة ارتطام القذيفة بالأرض تعادل

$$𝑣_{tot}= 43\; 𝑚/𝑠\;\;\;\;\;\;-C$$	$$𝑣_{tot}= 67 \;𝑚/𝑠\;\;\;\;\;\;-A$$
$$𝑣_{tot}= 31\; 𝑚/𝑠 \;\;\;\;\;\;-D$$	$$𝑣_{tot}=50 \;𝑚/𝑠 \;\;\;\;\;\;-B$$

اضغط هنا تظهر طريقة الحل

أختر الإجابة الصحيحة

---

A

---

B

---

C

---

D

---

20

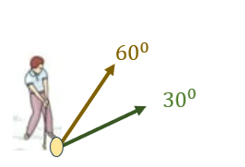
في لعبة الغولف تم ضرب الكرة من سطح الأرض مرتين وبنفس السرعة الابتدائية ولكن بزوايا مختلفة $$𝜃_1=30^0\;\;\;\;\;𝜃_2=60^0$$ وتم المقارنة بين مدى الكرتين فإن أحد الإجابات تعبر عن المدى الأفقي للكرتين

$$R_1>R_2 -C$$	$$R_1=R_2 -A$$
البيانات غير كافية لتحديد المدى الأفقي -D	$$R_2>R_1 -B$$

اضغط هنا تظهر طريقة الحل

أختر الإجابة الصحيحة

---

A

---

B

---

C

---

D

---

21

ثلاث قوى متلاقية أثرت على جسم كما في الشكل أدناه
فإن محصلة القوى على المحور الأفقي وعلى المحور الرأسي تعادل يعادل

$$FX=131.2 \;\;\;\;\;\; FY=10 -C$$	$$FX=11.2 \;\;\;\;\;\; FY=40 -A$$
$$FX=0 \;\;\;\;\;\; FY=0 -D$$	$$FX=91.2 \;\;\;\;\;\; FY=40-B$$

اضغط هنا تظهر طريقة الحل

أختر الإجابة الصحيحة

---

A

---

B

---

C

---

D

---

22

مستوى مائل خشن وضع جسم $$B$$ على المستوى المائل وترك لينزلق و بنفس اللحظة تم سحب جسم $$A$$ بحبل وهو موضوع فوق سطح اللجسم $$B$$ وبشكل يوازي السطح المائل نحو الأعلى فإن متجهات القوى المؤثرة على كل جسم

اضغط هنا تظهر طريقة الحل

أختر الإجابة الصحيحة

---

A

---

B

---

C

---

D

---

23

عندما يصل المظلي الساقط سقوط حر إلى السرعة الحدية فإن

$$Fd>Fg \;\;\;\;\;\;-C$$	$$Fg>Fd \;\;\;\;\;\;-A$$
$$Fg=Fd \;\;\;\;\;\;-D$$	$$Fg=Fd =0\;\;\;\;\;\;-B$$

اضغط هنا تظهر طريقة الحل

أختر الإجابة الصحيحة

---

A

---

B

---

C

---

D

---

24

مظلي كتلته 85 كيلو جرام يسقط سقوط حر بوضعية النسر ويداه مضمومتين إلى جانبه
إذا علمت أن كثافة الهواء ومعامل السحب والمساحة التي يشغلها تعادل $$𝜌=1.21 kg/m^3\;\;\;\;\;\;\;\;\;\;C=1 \;\;\;\;\;\;\;\;\;\;A=0.7 \;m^2$$ فإن السرعة الحدية للمظلي تعادل

$$v=44 \;m/s\;\;\;\;\;\;-C$$	$$v=50\;m/s\;\;\;\;\;\;-A$$
$$v=22 \;m/s\;\;\;\;\;\; -D$$	$$v=35 \;m/s \;\;\;\;\;\;-B$$

اضغط هنا تظهر طريقة الحل

أختر الإجابة الصحيحة

---

A

---

B

---

C

---

D

---

25

سيارة كتلتها $$m$$ تتحرك على طريق أفقي أملس وتتحرك بتسارع قدره
𝑎= 4 m / S²
تم تعلق سيارة مماثلة لها بحبل فإن كلا السيارتين تتحرك بتسارع مقداره

$$a= 1 \;\;m/s^2 \;\;\;\;\;\;-C$$	$$a=2\;\; m/s^2\;\;\;\;\;\;-A$$
$$a= 4\;\; m/s^2\;\;\;\;\;\;-D$$	$$a=3\;\; m/s^2 \;\;\;\;\;\;-B$$

اضغط هنا تظهر طريقة الحل

أختر الإجابة الصحيحة

---

A

---

B

---

C

---

D

---

26

أربع كرات كتلة كل منها 1.5 كيلو جرام تم ربطها ببعضها البعض بوساطة أربع حبال عديمة الكتلة وعلقت بالسقف كما في الشكل أدناه فإن قوة الشد المؤثرة على الخيط الثاني تعادل

$$𝐹_𝑔=𝐹_𝑇=58.86\; 𝑁 \;\;\;\;\;\;-C$$	$$𝐹_𝑔=𝐹_𝑇=29.43\; 𝑁\;\;\;\;\;\;\;-A$$
$$𝐹_𝑔=𝐹_𝑇=14.7\; 𝑁\; \;\;\;\;\;\;-D$$	$$𝐹_𝑔=𝐹_𝑇=44.15\; 𝑁\;\;\;\;\;\;-B$$

اضغط هنا تظهر طريقة الحل

أختر الإجابة الصحيحة

---

A

---

B

---

C

---

D

---

أجب عن الاسئلة التالية

$$1\star$$

متجهات أبعادها الديكارتية مبينه في الشكل بالاعتماد على بيانات الشكل أدناه حدد إحداثيات المتجه $$\vec A \;\;\;\;\;\;\;\;\;\; \vec B$$ $$.....................................\;\;\;\;............................................$$ $$.....................................\;\;\;\;............................................$$ $$.....................................\;\;\;\;............................................$$ $$.....................................\;\;\;\;............................................$$ أوجد بالرسم على الشبكة السابقة باستخدام مثلث المتجهات $$\vec K= \vec A\;-\vec B$$ $$\;\;\;\;\;\;\;\;\;\;$$ الاحداثيات الديكارتية للمتجهين $$\vec C(4\widehat x \;, 2 \widehat y)\;\;\;\;\;\;\;\;\; \vec D(4\widehat x \;, -4 \widehat y)$$ أوجد بالإحداثيات الديكارتية مقدار المتجه $$\vec k$$ حيث أن $$\vec k=\vec C+ 2\vec D$$ $$.....................................\;\;\;\;............................................$$ $$.....................................\;\;\;\;............................................$$ $$.....................................\;\;\;\;............................................$$ $$.....................................\;\;\;\;............................................$$ أوجد الزاوية التي يصنعها المتجه $$\vec D$$ مع المحور الأفقي الموجب بدوران عكس عقارب الساعة $$.....................................\;\;\;\;............................................$$ $$.....................................\;\;\;\;............................................$$

اضغط هنا تظهر طريقة الحل

$$2\star$$

الخط البياني التالي يبين العلاقة بين( السرعة –الزمن )
لدراجة تتحرك في بعد واحد
أحسب العجلة اللحظية في اللحظة $$t=8 s$$
$$........................................................................................$$ $$........................................................................................$$

اضغط هنا تظهر طريقة الحل

$$3\star$$

( X ) يحدد موقع جسم يتحرك على المحور
من خلال العلاقة $$X=9+10 𝑡-2𝑡^2$$ حيث تقدر $$X(m) , t(s)$$ حدد موقع الجسم عندما يصل إلى أقصى إزاحة $$........................................................................................$$ $$........................................................................................$$ $$........................................................................................$$ $$........................................................................................$$ $$........................................................................................$$

اضغط هنا تظهر طريقة الحل

$$4\star$$

قذفت كرة من سطح الأرض بسرعة ابتدائية مقدارها $$20\;\;m/s$$ احسب سرعة الكرة عند منتصف أقصى ارتفاع (بإهمال مقاومة الهواء ) $$g=9.81 m/s^2$$

$$........................................................................................$$ $$........................................................................................$$ $$........................................................................................$$ $$........................................................................................$$ $$........................................................................................$$

اضغط هنا تظهر طريقة الحل

$$5\star$$

يجري غزال في حديقة في بعدين $$X(t)=0.5.t^2+12t+15\;\;\;\;\;\;Y(t)=-0.3.t^2+6t+20$$ بحيث وجدة قياس $$X(m)\;\;\;Y(m)\;\;\;t(s)$$

احسب موقع الغزال في اللحظة $$t=8\;\;s$$

$$........................................................................................$$ $$........................................................................................$$ احسب السرعة للغزال في اللحظة $$t=8\;\;s$$ $$........................................................................................$$ $$........................................................................................$$ $$........................................................................................$$ $$........................................................................................$$ $$........................................................................................$$

اضغط هنا تظهر طريقة الحل

$$6\star$$

أطلق رامي السهم سهماً على هدف يبعد عنه 80 متر بحيث كان الهدف على نفس ارتفاع اطلاق السهم
احسب الزاوية التي يجب أن يطلق بها السهم ليضرب مركز الهدف إذا كانت سرعته البدائية للسهم $$v_0=30\;\;m/s$$ $$.....................................\;\;\;\;............................................$$ $$.....................................\;\;\;\;............................................$$ $$.....................................\;\;\;\;............................................$$ $$.....................................\;\;\;\;............................................$$ $$.....................................\;\;\;\;............................................$$ $$.....................................\;\;\;\;............................................$$ وجد عارضة مستندة على قواعد في منتصف المسافة بين الرامي والهدف وهي بشكل أفقي على ارتفاع $$3.5 \;\;m$$ فوق ارتفاع إطلاق السهم. هل سيمر السهم فوق ام تحت العارضة $$.....................................\;\;\;\;............................................$$ $$.....................................\;\;\;\;............................................$$ $$.....................................\;\;\;\;............................................$$

اضغط هنا تظهر طريقة الحل

$$7\star$$

في الشكل أدناه جسم كتلته 2.65 كيلو جرام وضع على مستوى أفقي خشن
أثرت علية قوة شد مقداها 20 نيوتن اتجاهها نحو اليمين تميل فوق الأفق بزاوية 30 درجة
فتحرك الجسم فإذا كان معامل الاحتكاك الحركي 0.625 الجسم حدد على الشكل القوي المؤثرة على الجسم
احسب التسارع الذي يتحرك به الجسم $$.........................................\;\;\;\;\;\;....................................$$ $$.........................................\;\;\;\;\;\;....................................$$ $$.........................................\;\;\;\;\;\;....................................$$ $$.........................................\;\;\;\;\;\;....................................$$ $$.........................................\;\;\;\;\;\;....................................$$

اضغط هنا تظهر طريقة الحل

$$8\star$$

ثلاث قوى متلاقية أثرت على جسم كما في الشكل أدناه أثرت على جسم فأصبح الجسم في حالة اتزان

حدد مقدار واتجاه القوة $$\vec F_2=?$$ $$.....................................\;\;\;\;............................................$$ $$.....................................\;\;\;\;............................................$$ $$.....................................\;\;\;\;............................................$$ $$.....................................\;\;\;\;............................................$$ $$.....................................\;\;\;\;............................................$$

اضغط هنا تظهر طريقة الحل

اكتب تعليقا واذا كان هناك خطأ اكتبه وحدد مكانه Write a comment, and if there is mistake, write and specify its location

Social Media

Created By Themes | Distributed By Blogger

Contact form