Physics
📄 اطبع pdf
00971504825082
الحركة الدائرية
الإحداثيات القطبية والديكارتية
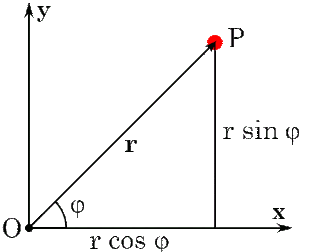
الإحداثيات القطبية
لدراسة الحركة الدائرية نستخدم الاحداثيات القطبية لتحديد موقع الجسم
حيث نستخدم الزوج
\[ r\;\;\;\;\;\; ,\;\;\;\;\;\; 𝜃\]
نسمي نقطة الأصل القطب 
والمحور القطبي هوالمحور الموجب
\[X\]
بعد الجسم عن القطب هي
\[r\]
والزاوية التي يصنعها البعد مع المجور القطبي بدوران عكس عقارب الساعة
\[𝜃\]
الأحداثيات الديكارتية
لتحديد موضع نقطة على مستوى ثنائي الأبعاد ، نستخدم رقمين تسمى الإحداثيات الديكارتي 
الرقم لأول مدى المسافة على طول المحور الأفقي
\[X\]
الرقم الثاني مدى المسافة على طول المحور الرأسي
\[Y\]
التحويل من الإحداثيات الديكارتية إلى القطبية أو العكس
للتحويل بين النوعين من الإحداثيات نستخدم المثلث التالي
للتحويل من الإحداثيات القطبية إلى الإحداثيات الديكارتي
لدينا الأن
\[ r\;\;\;\;\;\; ,\;\;\;\;\;\; 𝜃\]
المطلوب
\[ X\;\;\;\;\;\; ,\;\;\;\;\;\; Y\]
من المثلث السابق > \[X= r . Cos {𝜃}\]\[Y= r . Sin {𝜃}\]
للتحويل من الإحداثيات الديكارتي إلى الإحداثيات القطبية
لدينا الأن
\[ X\;\;\;\;\;\; ,\;\;\;\;\;\; Y\]
المطلوب
\[ r\;\;\;\;\;\; ,\;\;\;\;\;\; 𝜃\]
من المثلث السابق
\[r= \sqrt{X^2 + Y^2}\]\[𝜃={ \tan{^-1 }{\frac{Y}{X}}}\]
1مثال
الإحداثيات الديكارتية لجسم هي
(-3 , 10 )
فكم الإحداثيات القطبية له
اضغط هنا تظهر طريقة الحل
أختر الإجابة الصحيحة
2مثال
الإحداثيات القطبية لجسم هي
(13 , 22.6 0 )
فكم الإحداثيات الديكارتية له
اضغط هنا تظهر طريقة الحل
أختر الإجابة الصحيحة
الإحداثيات الزاوية والإزاحة الزاوية
أذا تحرك جسم من نقطة الى اخرى وقطع قوس طوله
\[S\] على محيط دائره نصف قطرها
\[r\] فإن الزاويه التي تقابل القوس تسمى بالازاحه الزاويه ويرمز لها بالرمز
\[𝜃\] \[𝜃 =\frac{s}{r}\] 
الإزاحة الزاوية كمية متجهه إذا كان الدوران عكس عقارب الساعة تأخذ إشارة موجبة وإذا كان الدوران مع عقارب الساعة تأخذ إشارة موجبة
يمثل الراديان الوحدة لقياس الإحداثيات الزاوية
قد تجد الإزاحة الزاوية بوحدة الدرجات او بوحدة الدورات
\[rev\] يتم تحويل الزاوية إلى الراديان حسب معاملات التحويل التالية
معامل التحويل من الدورات إلى الراديان
معامل التحويل من الدرجات إلى الراديان
\[2𝜋 (rad)= 1 rev\]
\[𝜋 (rad )= 180^0\]
مثال :جسم يتحرك حركة دائرية قطع إزاحة زاوية قدرها 2.25 دورة فكم يعادل بالراديان
مثال : جسم قطع إزاحة زاوية 120 درجة فكم يعادل
بوحدة الراديان
\[ 𝜃 = 2.25 × 2𝜋 =14.13 rad \]
\[ 𝜃 = 120 ^0 × \frac{𝜋}{180}=2.1 rad \]
السرعة الزاوية التردد الزاوي الزمن الدوري
التجربة 1 قياس السرعة الزاوية والتردد الزاوي والزمن الدوري
محاكاة الحركة الدائرية المنتظمة
تجربة الحركة الدائرية المنتظمة
الزمن: 0 ثانية
النتائج:
الإزاحة الزاوية الابتدائية (θ₁): 0 راديان
الزمن الابتدائي (t₁): 0 ثانية
الإزاحة الزاوية النهائية (θ₂): 0 راديان
الزمن النهائي (t₂): 0 ثانية
الفترة الزمنية
الإزاحة الزاوية النهائية
الإزاحة الزاوية الإبتدئية
\[t_2 -t_1= ....s\]
\[𝜃_2= .....rad\]
\[𝜃_1= ....rad\]
السرعة الزاوية
اتجاه السرعة الزاوية
\[W= \frac{𝜃_2 - 𝜃_1}{t_2 -t_1}= ......rad/s \] السرعة الزاوية معدل تغير الزاوية خلال الزمن
( T )زمن الدورة الواحدة
(f )عدد الدورات في الثانية يسمى التردد الزاوي
\[f= \frac{1}{T}\]\[W= \frac{𝜃_2 - 𝜃_1}{t_2 -t_1}=\frac{2𝜋}{T}=2𝜋f\]
إذا كان الدوران عكس عقارب الساعة 
إذا كان الدوران بإتجاه عقارب الساعة
معلومات مفيدة: السرعة الزاوية والسرعة الخطية
يكون متجه السرعة الخطية مماساً لمحيط الدائرة دائماً ويشير إلى اتجاه الحركة وينطبق على متجه الوحدة المماسي
لاحظ يكون متجه السرعة الخطية عمودياً دائماً على متجه الموقع القطري
\[\vec r . \vec v=0\]
يوجد علاقة بين السرعة الخطية والسرعة الزاوية
\[v=r.w\]
3مثال
يتحرك جسم حركه دائريه منتظمة بحيث يعمل
ثلاث دورات ونصف عكس عقارب الساعة كل 2 ثانية فان سرعته الزاوية
بوحدة \[\frac{rad}{s}\]
اضغط هنا تظهر طريقة الحل
أختر الإجابة الصحيحة
4مثال
مروحه تدور بسرعه بزاويه قدرها
\[60 𝜋 \; rad/s \]
فان تردد المروحة يعادل
اضغط هنا تظهر طريقة الحل
أختر الإجابة الصحيحة
5مثال
يتحرك جسم في مسار دائري منتظم نصف قطره
\[100\;cm\]حيث كان زمنه الدوري
\[2\;s\] فان سرعته الخطيه بوحدة
\[m/s\]
تعادل
اضغط هنا تظهر طريقة الحل
أختر الإجابة الصحيحة
🧮 Calculator
الحركة الدائرية |
الإحداثيات القطبية
لدراسة الحركة الدائرية نستخدم الاحداثيات القطبية لتحديد موقع الجسم
حيث نستخدم الزوج
\[ r\;\;\;\;\;\; ,\;\;\;\;\;\; 𝜃\]
نسمي نقطة الأصل القطب والمحور القطبي هوالمحور الموجب
\[X\]
بعد الجسم عن القطب هي
\[r\]
والزاوية التي يصنعها البعد مع المجور القطبي بدوران عكس عقارب الساعة
\[𝜃\]
الأحداثيات الديكارتية
لتحديد موضع نقطة على مستوى ثنائي الأبعاد ، نستخدم رقمين تسمى الإحداثيات الديكارتي الرقم لأول مدى المسافة على طول المحور الأفقي
\[X\]
الرقم الثاني مدى المسافة على طول المحور الرأسي
\[Y\]
التحويل من الإحداثيات الديكارتية إلى القطبية أو العكس
للتحويل بين النوعين من الإحداثيات نستخدم المثلث التالي
للتحويل من الإحداثيات القطبية إلى الإحداثيات الديكارتي
لدينا الأن
\[ r\;\;\;\;\;\; ,\;\;\;\;\;\; 𝜃\]
المطلوب
\[ X\;\;\;\;\;\; ,\;\;\;\;\;\; Y\]
من المثلث السابق > \[X= r . Cos {𝜃}\]\[Y= r . Sin {𝜃}\] للتحويل من الإحداثيات الديكارتي إلى الإحداثيات القطبية لدينا الأن \[ X\;\;\;\;\;\; ,\;\;\;\;\;\; Y\] المطلوب \[ r\;\;\;\;\;\; ,\;\;\;\;\;\; 𝜃\]
من المثلث السابق
\[r= \sqrt{X^2 + Y^2}\]\[𝜃={ \tan{^-1 }{\frac{Y}{X}}}\]
الإحداثيات الديكارتية لجسم هي
(-3 , 10 )
فكم الإحداثيات القطبية له
اضغط هنا تظهر طريقة الحل
أختر الإجابة الصحيحة
الإحداثيات القطبية لجسم هي
(13 , 22.6 0 )
فكم الإحداثيات الديكارتية له
اضغط هنا تظهر طريقة الحل
أختر الإجابة الصحيحة
أذا تحرك جسم من نقطة الى اخرى وقطع قوس طوله \[S\] على محيط دائره نصف قطرها \[r\] فإن الزاويه التي تقابل القوس تسمى بالازاحه الزاويه ويرمز لها بالرمز \[𝜃\] \[𝜃 =\frac{s}{r}\]
الإزاحة الزاوية كمية متجهه إذا كان الدوران عكس عقارب الساعة تأخذ إشارة موجبة وإذا كان الدوران مع عقارب الساعة تأخذ إشارة موجبة
يمثل الراديان الوحدة لقياس الإحداثيات الزاوية
قد تجد الإزاحة الزاوية بوحدة الدرجات او بوحدة الدورات \[rev\] يتم تحويل الزاوية إلى الراديان حسب معاملات التحويل التالية
معامل التحويل من الدورات إلى الراديان |
معامل التحويل من الدرجات إلى الراديان |
\[2𝜋 (rad)= 1 rev\] |
\[𝜋 (rad )= 180^0\] |
مثال :جسم يتحرك حركة دائرية قطع إزاحة زاوية قدرها 2.25 دورة فكم يعادل بالراديان |
مثال : جسم قطع إزاحة زاوية 120 درجة فكم يعادل بوحدة الراديان |
\[ 𝜃 = 2.25 × 2𝜋 =14.13 rad \] |
\[ 𝜃 = 120 ^0 × \frac{𝜋}{180}=2.1 rad \] |
التجربة 1 قياس السرعة الزاوية والتردد الزاوي والزمن الدوري
تجربة الحركة الدائرية المنتظمة
النتائج:
الإزاحة الزاوية الابتدائية (θ₁): 0 راديان
الزمن الابتدائي (t₁): 0 ثانية
الإزاحة الزاوية النهائية (θ₂): 0 راديان
الزمن النهائي (t₂): 0 ثانية
الفترة الزمنية |
الإزاحة الزاوية النهائية |
الإزاحة الزاوية الإبتدئية |
||||||
\[t_2 -t_1= ....s\] |
\[𝜃_2= .....rad\] |
\[𝜃_1= ....rad\] |
||||||
السرعة الزاوية |
اتجاه السرعة الزاوية |
\[W= \frac{𝜃_2 - 𝜃_1}{t_2 -t_1}= ......rad/s \] السرعة الزاوية معدل تغير الزاوية خلال الزمن |
|
يكون متجه السرعة الخطية مماساً لمحيط الدائرة دائماً ويشير إلى اتجاه الحركة وينطبق على متجه الوحدة المماسي
لاحظ يكون متجه السرعة الخطية عمودياً دائماً على متجه الموقع القطري
\[\vec r . \vec v=0\]
يوجد علاقة بين السرعة الخطية والسرعة الزاوية
يتحرك جسم حركه دائريه منتظمة بحيث يعمل
ثلاث دورات ونصف عكس عقارب الساعة كل 2 ثانية فان سرعته الزاوية
بوحدة \[\frac{rad}{s}\]
أختر الإجابة الصحيحة مروحه تدور بسرعه بزاويه قدرها
\[60 𝜋 \; rad/s \]
فان تردد المروحة يعادل
أختر الإجابة الصحيحة يتحرك جسم في مسار دائري منتظم نصف قطره
\[100\;cm\]حيث كان زمنه الدوري
\[2\;s\] فان سرعته الخطيه بوحدة
\[m/s\]
تعادل
أختر الإجابة الصحيحة
\[v=r.w\]
اضغط هنا تظهر طريقة الحل
اضغط هنا تظهر طريقة الحل
اضغط هنا تظهر طريقة الحل
No comments:
Post a Comment