Physics
📄 اطبع pdf
00971504825082
التيار المتردد
Alternating Current
دائرة تيار متردد متصلة على التوالي تحتوي على ملف ومكثف ومقاوم أومي
A series AC circuit containing a coil, a capacitor, and an ohmic resistor.
معلومات تم التوصل لها
Information derived
( C ) مكثف في دائرة متردد( C ) Capacitor in an AC circuit
( L ) ملف نقي في دائرة تيار متردد( L ) Pure coil in an AC circuit
( R ) مقاومة أومية في دائرة تيار متردد( R ) Ohmic resistance in an AC circuit
المكثف جهده متأخر في الطور على التيار بمقدار \[\frac{π}{2}\]Capacitor voltage lags behind the current in phase by \[\frac{π}{2}\]
الملف جهده متقدم في الطور على التيار بمقدار \[\frac{π}{2}\]Coil voltage leads the current in phase by \[\frac{π}{2}\]
المقاومة جهدها متفق في الطور مع التيارResistor voltage is in phase with the current
في دائرة ملف ومكثف ومقاوم أومي التوصيل على التوالي
In a circuit with a coil, capacitor, and ohmic resistor connected in series
التيار ثابت معادلة التيار تكون من الشكل
The current is constant. The current equation takes the form
\(𝑖 (t) = 𝐼_𝑚 sin (𝜔t ± ∅ )\)
قد يكون التيار متقدم في الطور عن الجهد أو يكون متأخر في الطور
The current may lead or lag the voltage in phase
السؤال كيف نجد فرق الجهد الكلي و الممانعة الكلية وزاوية الطور بين التيار والجهد
The question is: how do we find the total potential difference, the total impedance, and the phase angle between the current and the voltage?
\[ 𝑉_m(tot) ≠𝑉_𝑅 + 𝑉_𝐶 + 𝑉_𝐿 \]
\[ Z ≠𝑅 + X_𝐶 + X_𝐿 \]
في هذه المحاكاة قم بإختيار دائرةIn this simulation, select an \[RLC\]
قم بتوصيل ملف ومقاوم ومكثف على التوالي بمصدر تيار مترددConnect a coil, resistor, and capacitor in series to an AC source.
اضغط على كل جزء وقم بتسجيل كلا من قيمة من سعة المكثف ومعامل الحث الذاتي للملف والمقاومة الأومية وقيمة أعظم جهد للمصدر وتردد المصدر
Click on each component and record the capacitance value, the self-inductance coefficient of the coil, the ohmic resistance, the maximum source voltage, and the source frequency.
استخدم الأميتر وراسم الأشارة للتيار لتحديد القيمة العظمى لتيار المصدر وقس قيمة أعظم تيار في كل جزء من الدائرة وسجل القيم
Use the ammeter and the current oscilloscope to determine the maximum source current and measure the maximum current in each part of the circuit, recording the values.
استخدم الفولتوميتر وراسم الاشارة للجهد لتحديد قيمة أعظم جهد للمصدر وأعظم جهد لكل جزء من الدائرة
Use the voltmeter and the voltage oscilloscope to determine the maximum source voltage and the maximum voltage across each part of the circuit.
احسب المفاعلة الحثية والمفاعلة السعويةCalculate the inductive reactance and capacitive reactance.
أحسب أعظم قيمة للجهد في كل جزء وقارنها بالقياسات التي قمت بهاCalculate the maximum voltage across each part and compare it with the measurements you took.
استخدم التمثيل الأتجاهي لإيجاد قيمة الجهد الكليUse the phasor diagram to find the total voltage.
📊 التجربة العملية: معطيات الدائرة (RLC)📊 Practical Experiment: (RLC) Circuit Data
القيم المقاسة أو المعطاة في التجربةValues measured or given in the experiment
سعة المكثفCapacitance
(C) μF
معامل الحث الذاتيSelf-inductance
(L) mH
المقاومة الأوميةOhmic Resistance
(R) Ω
أعظم قيمة لتيار المصدرMaximum Source Current
(Im) A
أعظم قيمة لجهد المصدرMaximum Source Voltage
(Vm) V
تردد المصدرSource Frequency
(f) Hz
🧮 القيم المطلوب حسابها (من قبل الطالب)🧮 Required Values to Calculate (by the student)
✏️ قاعدة التصحيح: إذا كان الفرق بين إجابتك والقيمة الصحيحة أقل من 0.5، تعتبر الإجابة صحيحة ✅Correction rule: If the difference between your answer and the correct value is less than 0.5, your answer is considered correct ✅
المفاعلة السعويةCapacitive Reactance
\[ X_C = \frac{1}{2\pi f C} \]
المفاعلة الحثيةInductive Reactance
\[ X_L = 2\pi f L \]
أعظم قيمة لجهد المقاومMaximum Resistor Voltage
\[ V_R = I_m \cdot R \]
أعظم قيمة لجهد المكثفMaximum Capacitor Voltage
\[ V_C = I_m \cdot X_C \]
أعظم قيمة لجهد الملفMaximum Coil Voltage
\[ V_L = I_m \cdot X_L \]
استخدم القيم التي تم حسابها معتبرا الجهود كميات متجهه ومثلها على الخط البياني التالي
Use the calculated values considering the voltages as vectors and represent them on the following phasor diagram.
أوجد أولاFirst, find
VL - VC = ...............
ناتج الطرح باتجاه الأكبرSubtraction result in the direction of the larger.
(VR) انقل متجهة الطرح على رأس المتجه(VR) Translate the subtraction vector to the head of VR.
أوجد محصلة المتجهين المتعامدينFind the resultant of the two perpendicular vectors.
\[(V_ m)^2=(V_ R)^2 + ( V_ L - V_ C)^2\]
\[(V_ m)= ............\]
حساب المعوقة (ممانعة الدائرة الكلية)Calculation of the impedance (total circuit impedance).
(Z) يرمز لها بالرمزDenoted by (Z).
\[(V_ m)^2=(V_ R)^2 + ( V_ L - V_ C)^2\]
\[(I_ m)^2 . Z^2=(I_ R)^2 .R^2+ ( I_ L.XL - I_ C.XC)^2\]
التيار متساوي لأن التوصيل على التوالي يمكن الاختصارThe current is equal because the connection is in series; it can be simplified.
\[ Z^2= R^2+ (XL - XC)^2\]
زاوية الطورPhase Angle
وهي الزاوية بين التيار وفرق الجهدIt is the angle between the current and the voltage.
من خلال المتجهات التي تم رسمهاFrom the drawn vectors:
\[ ∅ = \tan^{-1} \frac{( V_ L - V_ C)}{V_ R}\]
أو من خلال الممانعات يمكن حساب زاوية الطورOr from the impedances, the phase angle can be calculated
\[ ∅ = \tan^{-1} \frac{( XL - XC)}{R}\]
إذا كانت زاوية الطور بإشارة سالبة فإن التيار متقدم على الجهدIf the phase angle has a negative sign, the current leads the voltage.
إذا كانت زاوية الطور بإشارة موجبة فإن الجهد متقدم على التيارIf the phase angle has a positive sign, the voltage leads the current.
1 مثالExample 1
دائرة ملف ومقاوم ومكثف \[RLC\] متصلة على التوالي بمصدر تيار متردد فكانت مفاعلة الملف أكبر من مفاعلة المكثف
A series RLC circuit (coil, resistor, capacitor) is connected to an AC source. The inductive reactance is greater than the capacitive reactance.
\[X_L > X_C\]
فإن أحد الإجابات التالية صحيحةWhich of the following answers is correct?
أختر الإجابة الصحيحةChoose the correct answer
A
الجهد يسبق التيار بمقدار \[θ\]Voltage leads the current by \[θ\]
B
التيار والجهد متفقان في الطورVoltage and current are in phase
C
التيار يسبق الجهد بمقدار \[θ\]Current leads the voltage by \[θ\]
D
الجهد يسبق التيار بمقدار \[π/2\]Voltage leads the current by \[π/2\]
اضغط هنا تظهر طريقة الحلClick here to view the solution
2 مثالExample 2
في الشكل المجاور دائرة \[RLC\] متصلة بمصدر تيار متردد معادلته
In the adjacent RLC circuit, connected to an AC source with the equation
\[V(t) = 210 \sin(300 t)\]
فإذا علمت أنGiven that
\[L = 0.5 \; H \quad C = 5 \; \mu F \quad R = 150 \; \Omega\]
فإن قيمة المعاوقة للدائرة تعادلThe impedance of the circuit is
أختر الإجابة الصحيحةChoose the correct answer
A
\[Z = 620 \; \Omega\]
B
\[Z = 538 \; \Omega\]
C
\[Z = 335 \; \Omega\]
D
\[Z = 427 \; \Omega\]
اضغط هنا تظهر طريقة الحلClick here to view the solution
دائرة تيار متردد (ملف - مقاوم)AC circuit (coil - resistor)
دائرة تيار متردد (مقاوم - مكثف)AC circuit (resistor - capacitor)
دائرة الرنينResonance Circuit
يتم استخدام دائرة الرنين في أجهزة الاستقبال الإذاعي والتلفزيونيResonant circuits are used in radio and television receivers.
يتم تغيير التردد أو تغيير سعة المكثف أو تغيير معامل الحث الذاتي للملف حتى نحصل على الرنين
The frequency, the capacitance, or the self-inductance of the coil is changed to achieve resonance.
في العادة يتم تغيير التردد حتى تنخفض ممانعة الدائرة وتسمح بعبور تيار واحد قادم من اللاقط له تردد يعادل تردد الدائرة
Typically, the frequency is changed until the circuit's impedance decreases and allows a single current, coming from the antenna with a frequency equal to the circuit's frequency, to pass.
(RLC) في هذه المحاكاة قم بإختيار دائرة(RLC) In this simulation, select a circuit.
قم بتوصيل ملف ومقاوم ومكثف على التوالي بمصدر تيار مترددConnect a coil, resistor, and capacitor in series to an AC source.
غيّر من تردد المصدر حتى تصبحChange the source frequency until
XL = XC
عندها نقول حدث الرنينAt this point, resonance is said to occur.
عندها تصبح ممانعة الدائرة أقل ما يمكنThen, the circuit's impedance becomes as small as possible.
Z = R
وبالتالي يصبح التيار المار في الدائرة أكبر ما يمكنThus, the current flowing in the circuit becomes as large as possible.
\[I_ m =\frac{ V_ m}{R}\]
عند الرنين تكونAt resonance, \[V_L = V_C\]
\[ V_m = V_R \]
وكأن الدائرة تصبح بها فقط مقاومة ويكونAs if the circuit only contains resistance, and the
التيار والجهد متفقان في الطورcurrent and voltage are in phase.
وبالتالي فإن تردد الرنين للدائرةTherefore, the resonance frequency of the circuit is
\[f_ 0 = \frac{1}{2\pi\sqrt{LC}}\]
3 مثالExample 3
دائرة ملف ومقاوم ومكثف \[RLC\] متصلة بمصدر تيار متردد فرق جهده الأعظمي يعادل \[V=240 V \]وفرق الجهد الأعظمي للمقاوم \[VR=120V\] تم تغيير تردد المصدر حتى أصبح فرق الجهد الأعظمي للملف يساوي فرق الجهد الأعظمي للمكثف \[VL = VC\] فإن أعظم قيمة يصل إليها التيار المار في الدائرة علماً بأن \[R=160 Ω\]
An RLC circuit (coil, resistor, capacitor) connected to an AC source with a maximum voltage \[V=240 V\]and the maximum voltage across the resistor is \[VR=120V.\] The source frequency was changed until the maximum voltage across the coil equals the maximum voltage across the capacitor \[VL = VC\] Find the maximum current passing through the circuit. Given that \[R=160 Ω\]
أختر الإجابة الصحيحةChoose the correct answer
A
\[I_m = 3\;A\]
B
\[I_m = 1.5\;A\]
C
\[I_m = 2\;A\]
D
\[I_m = 0.5\;A\]
اضغط هنا تظهر طريقة الحلClick here to view the solution
4 مثالExample 4
دائرة رنين \[RLC\]متصلة بهوائي وتحتوي على ملف معامل الحث الذاتي \[L=0.03H\] ومكثف سعته \[C=2μF \]فإنها قادرة على استقبال موجة ترددها
A series RLC resonant circuit connected to an antenna. It contains a coil with self-inductance \[L=0.03H\] and a capacitor with capacitance \[C=2μF\] The frequency of the wave it can receive is
أختر الإجابة الصحيحةChoose the correct answer
A
\[f = 320\;Hz\]
B
\[f = 650\;Hz\]
C
\[f = 425\;Hz\]
D
\[f = 520\;Hz\]
اضغط هنا تظهر طريقة الحلClick here to view the solution
المحولاتTransformers
يستخدم المحول لرفع وخفض الجهد الكهربائيTransformers are used to step up or step down electrical voltage.
يتكون المحول منA transformer consists of:
ملف ابتدائي متصل بمصدر تيار مترددA primary coil connected to an AC source.
ملف ثانوي متصل بجهازA secondary coil connected to a load.
نواة من الحديدAn iron core.
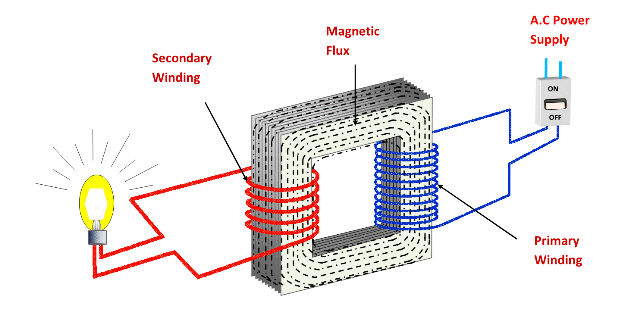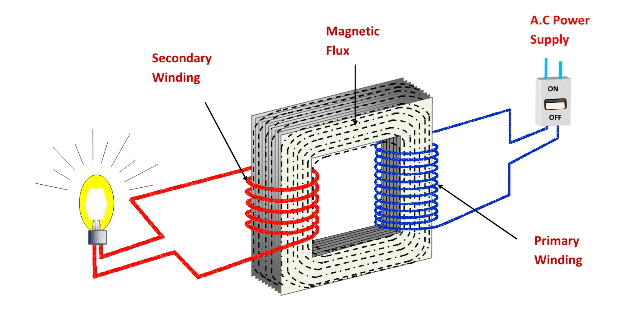
يعتمد في عمله على ظاهرة الحث المتبادلIts operation depends on the phenomenon of mutual induction.
نتيجة تغير التيار في الملف الابتدائي يتغير التدفق على الملف الثانوي ويتولد فرق جهد مستحث وتيار مستحث
As a result of the current change in the primary coil, the magnetic flux through the secondary coil changes, inducing a voltage and a current.
الملف الابتدائي والثانوي لهما نفس تغير التدفق بسبب وجود نواة الحديد
The primary and secondary coils experience the same change in flux due to the iron core:
\[V_{emf}=\frac{d∅_B}{dt}\]
فيكون فرق الجهد المستحث للملف الابتدائي والثانويThus, the induced voltage for the primary and secondary coils is:
\[V_s= - N_s \frac{d∅_B}{dt}\]\[V_p= - N_p \frac{d∅_B}{dt}\] وبقسمة المعادلتين على بعضهما نحصل علىDividing the two equations yields:
\[\frac{N_S}{N_P}=\frac{V_S}{V_P}\]
إذا كان عدد لفات الملف الابتدائي أكبر من الثانوي فإن المحول خافض للجهدIf the number of turns in the primary coil is greater than that in the secondary, the transformer is a step-down transformer.
إذا كان عدد لفات الملف الابتدائي أصغر من الثانوي فإن المحول رافع للجهدIf the number of turns in the primary coil is less than that in the secondary, the transformer is a step-up transformer.
عند وصل جهاز أو ما يسمى مقاوم في الملف الثانوي سيكون هناك قدرة في الملف الثانوي
When a load (resistor) is connected to the secondary coil, there will be power in the secondary coil:
\[P_S=I_S.V_S\]
وهذا التيار يولد مجالاً مغناطيسياً في الملف الثانوي يعمل على توليد فرق جهد مستحث في الملف الابتدائي محافظاً على الجهد الأصلي
This current generates a magnetic field in the secondary coil, which induces a voltage in the primary coil, maintaining the original voltage.
في المحولات المثاليةIn ideal transformers:
\[P_S=P_P \]\[I_S.V_S=I_P.V_P\]\[\frac{I_S}{I_P}=\frac{V_P}{V_S}=\frac{N_P}{N_S}\]
من خلال العلاقة العكسية بين الجهد والتيار فإن المحول الرافع للجهد هو خافض للتيار والخافض للجهد هو رافع للتيار
Due to the inverse relationship between voltage and current, a step-up transformer steps down the current, and a step-down transformer steps up the current.
معلومة مفيدةUseful Information
محولات العزل هي محولات لا ترفع ولا تخفض الجهد ويكون عدد لفات الملف الابتدائي والثانوي متساوية ويستخدم في عزل دائرة عن أخرى في الأجهزة المهمة حتى لا يحدث تداخل في التيارات
Isolation transformers are transformers that neither step up nor step down voltage. The number of turns in the primary and secondary coils is equal. They are used to isolate one circuit from another in critical equipment to prevent current interference.
يمكن حساب التيار في الملف الابتدائي من خلال العلاقةThe current in the primary coil can be calculated using the relation:
\[I_P=(\frac{N_S}{N_P})^2 \cdot \frac{V_P}{R}\]
يمكن حساب المقاومة الفعالة في الملف الابتدائي من خلال العلاقةThe effective resistance in the primary coil can be calculated using the relation:
\[R_P=(\frac{N_P}{N_S})^2 \cdot R \]
التيار المتردد Alternating Current |
( C ) مكثف في دائرة متردد( C ) Capacitor in an AC circuit |
( L ) ملف نقي في دائرة تيار متردد( L ) Pure coil in an AC circuit |
( R ) مقاومة أومية في دائرة تيار متردد( R ) Ohmic resistance in an AC circuit |
|
|
|
في دائرة ملف ومكثف ومقاوم أومي التوصيل على التوالي In a circuit with a coil, capacitor, and ohmic resistor connected in series
التيار ثابت معادلة التيار تكون من الشكل The current is constant. The current equation takes the form
\(𝑖 (t) = 𝐼_𝑚 sin (𝜔t ± ∅ )\)
قد يكون التيار متقدم في الطور عن الجهد أو يكون متأخر في الطور The current may lead or lag the voltage in phase
السؤال كيف نجد فرق الجهد الكلي و الممانعة الكلية وزاوية الطور بين التيار والجهد The question is: how do we find the total potential difference, the total impedance, and the phase angle between the current and the voltage?
\[ 𝑉_m(tot) ≠𝑉_𝑅 + 𝑉_𝐶 + 𝑉_𝐿 \]
\[ Z ≠𝑅 + X_𝐶 + X_𝐿 \]
في هذه المحاكاة قم بإختيار دائرةIn this simulation, select an \[RLC\]
قم بتوصيل ملف ومقاوم ومكثف على التوالي بمصدر تيار مترددConnect a coil, resistor, and capacitor in series to an AC source.
اضغط على كل جزء وقم بتسجيل كلا من قيمة من سعة المكثف ومعامل الحث الذاتي للملف والمقاومة الأومية وقيمة أعظم جهد للمصدر وتردد المصدر Click on each component and record the capacitance value, the self-inductance coefficient of the coil, the ohmic resistance, the maximum source voltage, and the source frequency.
استخدم الأميتر وراسم الأشارة للتيار لتحديد القيمة العظمى لتيار المصدر وقس قيمة أعظم تيار في كل جزء من الدائرة وسجل القيم Use the ammeter and the current oscilloscope to determine the maximum source current and measure the maximum current in each part of the circuit, recording the values.
استخدم الفولتوميتر وراسم الاشارة للجهد لتحديد قيمة أعظم جهد للمصدر وأعظم جهد لكل جزء من الدائرة Use the voltmeter and the voltage oscilloscope to determine the maximum source voltage and the maximum voltage across each part of the circuit.
احسب المفاعلة الحثية والمفاعلة السعويةCalculate the inductive reactance and capacitive reactance.
أحسب أعظم قيمة للجهد في كل جزء وقارنها بالقياسات التي قمت بهاCalculate the maximum voltage across each part and compare it with the measurements you took.
استخدم التمثيل الأتجاهي لإيجاد قيمة الجهد الكليUse the phasor diagram to find the total voltage.
📊 التجربة العملية: معطيات الدائرة (RLC)📊 Practical Experiment: (RLC) Circuit Data
القيم المقاسة أو المعطاة في التجربةValues measured or given in the experiment
| سعة المكثفCapacitance (C) μF |
معامل الحث الذاتيSelf-inductance (L) mH |
المقاومة الأوميةOhmic Resistance (R) Ω |
أعظم قيمة لتيار المصدرMaximum Source Current (Im) A |
أعظم قيمة لجهد المصدرMaximum Source Voltage (Vm) V |
تردد المصدرSource Frequency (f) Hz |
|---|---|---|---|---|---|
🧮 القيم المطلوب حسابها (من قبل الطالب)🧮 Required Values to Calculate (by the student)
✏️ قاعدة التصحيح: إذا كان الفرق بين إجابتك والقيمة الصحيحة أقل من 0.5، تعتبر الإجابة صحيحة ✅Correction rule: If the difference between your answer and the correct value is less than 0.5, your answer is considered correct ✅
| المفاعلة السعويةCapacitive Reactance \[ X_C = \frac{1}{2\pi f C} \] |
المفاعلة الحثيةInductive Reactance \[ X_L = 2\pi f L \] |
أعظم قيمة لجهد المقاومMaximum Resistor Voltage \[ V_R = I_m \cdot R \] |
أعظم قيمة لجهد المكثفMaximum Capacitor Voltage \[ V_C = I_m \cdot X_C \] |
أعظم قيمة لجهد الملفMaximum Coil Voltage \[ V_L = I_m \cdot X_L \] |
|---|---|---|---|---|
استخدم القيم التي تم حسابها معتبرا الجهود كميات متجهه ومثلها على الخط البياني التالي Use the calculated values considering the voltages as vectors and represent them on the following phasor diagram.
أوجد أولاFirst, find
VL - VC = ...............
ناتج الطرح باتجاه الأكبرSubtraction result in the direction of the larger.
(VR) انقل متجهة الطرح على رأس المتجه(VR) Translate the subtraction vector to the head of VR.
أوجد محصلة المتجهين المتعامدينFind the resultant of the two perpendicular vectors.
\[(V_ m)^2=(V_ R)^2 + ( V_ L - V_ C)^2\]
\[(V_ m)= ............\]
حساب المعوقة (ممانعة الدائرة الكلية)Calculation of the impedance (total circuit impedance).
(Z) يرمز لها بالرمزDenoted by (Z).
\[(V_ m)^2=(V_ R)^2 + ( V_ L - V_ C)^2\]
\[(I_ m)^2 . Z^2=(I_ R)^2 .R^2+ ( I_ L.XL - I_ C.XC)^2\]
التيار متساوي لأن التوصيل على التوالي يمكن الاختصارThe current is equal because the connection is in series; it can be simplified.
\[ Z^2= R^2+ (XL - XC)^2\]
زاوية الطورPhase Angle
وهي الزاوية بين التيار وفرق الجهدIt is the angle between the current and the voltage.
من خلال المتجهات التي تم رسمهاFrom the drawn vectors:
\[ ∅ = \tan^{-1} \frac{( V_ L - V_ C)}{V_ R}\]
أو من خلال الممانعات يمكن حساب زاوية الطورOr from the impedances, the phase angle can be calculated
\[ ∅ = \tan^{-1} \frac{( XL - XC)}{R}\]
إذا كانت زاوية الطور بإشارة سالبة فإن التيار متقدم على الجهدIf the phase angle has a negative sign, the current leads the voltage.
إذا كانت زاوية الطور بإشارة موجبة فإن الجهد متقدم على التيارIf the phase angle has a positive sign, the voltage leads the current.
دائرة ملف ومقاوم ومكثف \[RLC\] متصلة على التوالي بمصدر تيار متردد فكانت مفاعلة الملف أكبر من مفاعلة المكثف
A series RLC circuit (coil, resistor, capacitor) is connected to an AC source. The inductive reactance is greater than the capacitive reactance.
\[X_L > X_C\]
فإن أحد الإجابات التالية صحيحةWhich of the following answers is correct?
أختر الإجابة الصحيحةChoose the correct answer
اضغط هنا تظهر طريقة الحلClick here to view the solution
في الشكل المجاور دائرة \[RLC\] متصلة بمصدر تيار متردد معادلته
In the adjacent RLC circuit, connected to an AC source with the equation
\[V(t) = 210 \sin(300 t)\]
فإذا علمت أنGiven that
\[L = 0.5 \; H \quad C = 5 \; \mu F \quad R = 150 \; \Omega\]
فإن قيمة المعاوقة للدائرة تعادلThe impedance of the circuit is
أختر الإجابة الصحيحةChoose the correct answer
اضغط هنا تظهر طريقة الحلClick here to view the solution
دائرة تيار متردد (ملف - مقاوم)AC circuit (coil - resistor)
دائرة تيار متردد (مقاوم - مكثف)AC circuit (resistor - capacitor)
دائرة الرنينResonance Circuit
يتم استخدام دائرة الرنين في أجهزة الاستقبال الإذاعي والتلفزيونيResonant circuits are used in radio and television receivers.
يتم تغيير التردد أو تغيير سعة المكثف أو تغيير معامل الحث الذاتي للملف حتى نحصل على الرنين The frequency, the capacitance, or the self-inductance of the coil is changed to achieve resonance.
في العادة يتم تغيير التردد حتى تنخفض ممانعة الدائرة وتسمح بعبور تيار واحد قادم من اللاقط له تردد يعادل تردد الدائرة Typically, the frequency is changed until the circuit's impedance decreases and allows a single current, coming from the antenna with a frequency equal to the circuit's frequency, to pass.
(RLC) في هذه المحاكاة قم بإختيار دائرة(RLC) In this simulation, select a circuit.
قم بتوصيل ملف ومقاوم ومكثف على التوالي بمصدر تيار مترددConnect a coil, resistor, and capacitor in series to an AC source.
غيّر من تردد المصدر حتى تصبحChange the source frequency until
XL = XC
عندها نقول حدث الرنينAt this point, resonance is said to occur.
عندها تصبح ممانعة الدائرة أقل ما يمكنThen, the circuit's impedance becomes as small as possible. Z = R
وبالتالي يصبح التيار المار في الدائرة أكبر ما يمكنThus, the current flowing in the circuit becomes as large as possible. \[I_ m =\frac{ V_ m}{R}\]
عند الرنين تكونAt resonance, \[V_L = V_C\]
\[ V_m = V_R \]
وكأن الدائرة تصبح بها فقط مقاومة ويكونAs if the circuit only contains resistance, and the
التيار والجهد متفقان في الطورcurrent and voltage are in phase.
وبالتالي فإن تردد الرنين للدائرةTherefore, the resonance frequency of the circuit is
\[f_ 0 = \frac{1}{2\pi\sqrt{LC}}\]
دائرة ملف ومقاوم ومكثف \[RLC\] متصلة بمصدر تيار متردد فرق جهده الأعظمي يعادل \[V=240 V \]وفرق الجهد الأعظمي للمقاوم \[VR=120V\] تم تغيير تردد المصدر حتى أصبح فرق الجهد الأعظمي للملف يساوي فرق الجهد الأعظمي للمكثف \[VL = VC\] فإن أعظم قيمة يصل إليها التيار المار في الدائرة علماً بأن \[R=160 Ω\] An RLC circuit (coil, resistor, capacitor) connected to an AC source with a maximum voltage \[V=240 V\]and the maximum voltage across the resistor is \[VR=120V.\] The source frequency was changed until the maximum voltage across the coil equals the maximum voltage across the capacitor \[VL = VC\] Find the maximum current passing through the circuit. Given that \[R=160 Ω\]
أختر الإجابة الصحيحةChoose the correct answer
اضغط هنا تظهر طريقة الحلClick here to view the solution
دائرة رنين \[RLC\]متصلة بهوائي وتحتوي على ملف معامل الحث الذاتي \[L=0.03H\] ومكثف سعته \[C=2μF \]فإنها قادرة على استقبال موجة ترددها A series RLC resonant circuit connected to an antenna. It contains a coil with self-inductance \[L=0.03H\] and a capacitor with capacitance \[C=2μF\] The frequency of the wave it can receive is
أختر الإجابة الصحيحةChoose the correct answer
اضغط هنا تظهر طريقة الحلClick here to view the solution
المحولاتTransformers
يستخدم المحول لرفع وخفض الجهد الكهربائيTransformers are used to step up or step down electrical voltage.
يتكون المحول منA transformer consists of:
ملف ابتدائي متصل بمصدر تيار مترددA primary coil connected to an AC source.
ملف ثانوي متصل بجهازA secondary coil connected to a load.
نواة من الحديدAn iron core.
يعتمد في عمله على ظاهرة الحث المتبادلIts operation depends on the phenomenon of mutual induction.
نتيجة تغير التيار في الملف الابتدائي يتغير التدفق على الملف الثانوي ويتولد فرق جهد مستحث وتيار مستحث As a result of the current change in the primary coil, the magnetic flux through the secondary coil changes, inducing a voltage and a current.
الملف الابتدائي والثانوي لهما نفس تغير التدفق بسبب وجود نواة الحديد The primary and secondary coils experience the same change in flux due to the iron core: \[V_{emf}=\frac{d∅_B}{dt}\]
فيكون فرق الجهد المستحث للملف الابتدائي والثانويThus, the induced voltage for the primary and secondary coils is:
\[V_s= - N_s \frac{d∅_B}{dt}\]\[V_p= - N_p \frac{d∅_B}{dt}\] وبقسمة المعادلتين على بعضهما نحصل علىDividing the two equations yields:
\[\frac{N_S}{N_P}=\frac{V_S}{V_P}\]
إذا كان عدد لفات الملف الابتدائي أكبر من الثانوي فإن المحول خافض للجهدIf the number of turns in the primary coil is greater than that in the secondary, the transformer is a step-down transformer.
إذا كان عدد لفات الملف الابتدائي أصغر من الثانوي فإن المحول رافع للجهدIf the number of turns in the primary coil is less than that in the secondary, the transformer is a step-up transformer.
عند وصل جهاز أو ما يسمى مقاوم في الملف الثانوي سيكون هناك قدرة في الملف الثانوي When a load (resistor) is connected to the secondary coil, there will be power in the secondary coil: \[P_S=I_S.V_S\]
وهذا التيار يولد مجالاً مغناطيسياً في الملف الثانوي يعمل على توليد فرق جهد مستحث في الملف الابتدائي محافظاً على الجهد الأصلي This current generates a magnetic field in the secondary coil, which induces a voltage in the primary coil, maintaining the original voltage.
في المحولات المثاليةIn ideal transformers:
\[P_S=P_P \]\[I_S.V_S=I_P.V_P\]\[\frac{I_S}{I_P}=\frac{V_P}{V_S}=\frac{N_P}{N_S}\]
من خلال العلاقة العكسية بين الجهد والتيار فإن المحول الرافع للجهد هو خافض للتيار والخافض للجهد هو رافع للتيار Due to the inverse relationship between voltage and current, a step-up transformer steps down the current, and a step-down transformer steps up the current.
معلومة مفيدةUseful Information
محولات العزل هي محولات لا ترفع ولا تخفض الجهد ويكون عدد لفات الملف الابتدائي والثانوي متساوية ويستخدم في عزل دائرة عن أخرى في الأجهزة المهمة حتى لا يحدث تداخل في التيارات Isolation transformers are transformers that neither step up nor step down voltage. The number of turns in the primary and secondary coils is equal. They are used to isolate one circuit from another in critical equipment to prevent current interference.
يمكن حساب التيار في الملف الابتدائي من خلال العلاقةThe current in the primary coil can be calculated using the relation: \[I_P=(\frac{N_S}{N_P})^2 \cdot \frac{V_P}{R}\]
يمكن حساب المقاومة الفعالة في الملف الابتدائي من خلال العلاقةThe effective resistance in the primary coil can be calculated using the relation:
\[R_P=(\frac{N_P}{N_S})^2 \cdot R \]
محتوا جامعی بودخازن
ReplyDelete