طاقة الوضع و حفظ الطاقة ( 11A ) Potential energy and energy conservation

 

📄 اطبع pdf
00971504825082

<<<طاقة الوضع الجذبية والمرونية وعلاقتها بالشغل >>>

طاقة الوضع
وهي الطاقة التي يختزنها الجسم

طاقة الوضع الجذبية

هي الطاقة التي يختزنها جسم نتيجة موضعة من مستوى إختبار صفري
يرمز لطاقة الوضع الجذبية بالرمز $$Ug$$
وتقدر بوحدة الجول
في هذه المحاكاة دراسة العوامل المؤثرة على طاقة الوضع حيث يتم تغير كتلة الجسم وارتفاع الجسم ومجال الجاذبية يمكن أن تسحب الجسم نحو الاسفل سوف تشاهد أو نحو الأعلى بالضغط على الماوس وشاهد العلاقة بين التغير في طاقة الوضع والشغل
تغير موقع الجسم بشكل أفقي ورأسي $$continuous\;\; shifts$$ تغير موقع الجسم بشكل ورأسي $$vertical\;\; shift\;\; only$$ تغير موقع الجسم بشكل أفقي ورأسي $$horizontal\;\; shift\;\; only$$


مثال 1)كرة تركت تسقط من ارتفاع 2 متر من سطح الأرض انخفضت طاقة الوضع لها يمقدار 3 جول عندما وصلت الأرض أحسب كتلة الكرة



$$..................................$$ $$..................................$$

اضغط هنا تظهر طريقة الحل

معلومات مفيدة

مستوى الاختبار التي تكون فية طاقة الوضع التثاقلية معدومة نحن من يختاره

اي جسم موجود فوق مستوى الاختبار طاقة الوضع موجبة

اي جسم موجود تحت مستوى الاختبار طاقة الوضع سالبة

البندول
إذا كان مستوى الأختبار هو الموضع الرأسي للبندول

$$h = L - L .Cos ( 0 )$$
إذا كان مستوى الأختبار هو الموضع االأفقي للبندول

$$h = L Cos ( 0 )$$ وطاقة الوضع بإشارة سالبة

القوى المحافظة والقوى غير المحافظة


حتى نستطيع أن نحدد أن هذه القوى محافظة وهذه القوى غير محافظة ندرس الحالتين
الحالة الأولى : الصندوق التالي يتم رفعة عن سطح الأرض إلى ارتفاع
( h )
ويتم إعادتة إلى الأرض

شغل الوزن أثناء عملية الرفع
$$W _{Fg1} = Fg . d . Cos 𝜃 = m . g . h . Cos ( 180 ) = - m .g .h$$
شغل الوزن أثناء عملية إعادة الجسم إلى الأرض
$$W_{Fg2} = Fg . d . Cos 𝜃 = m . g . h . Cos ( 0 ) = m .g .h$$
الشغل الكلي المبذول
$$W _{ tot }= W_1 + W_2 = 0$$

نتائج مهمة

إن قوة الوزن تعتبر من القوى المحافظة

الشغل المبذول من قوة محافظة على مسار مغلق معدوم

شغل القوى المحافظة لا يعتمد على المسارالذي تسلكة وانما يعتمد على نقطة البداية والنهاية

الحالة الثانية : الصندوق التالي يتم دفعة على مستو خشن من الموضع $$A\Rightarrow B$$ ويتم إعادتة إلى نفس الموضع الذي بدء منه

الشغل المبذول من قوة الاحتكاك

شغل قوة الاحتكاك أثناء عملية دفع الصندوق نحو اليمين

$$W_ 1( F_K ) = - F_K .( X_B - X_A ) = - 𝜇_K . m . g . ( X_B - X_A )$$ شغل قوة الاحتكاك أثناء عملية دفع الصندوق نحو اليسار

$$W _2( F_K ) = F_K .( X_A - X_B ) = 𝜇𝑘 . m . g . ( X_A - X_B )$$

$$W 2( Fk ) = - 𝜇𝑘 . m . g . ( XB - XA )$$ الشغل الكلي المبذول $$w _{ tot} = W_1 + W_2 = -2 𝜇_K m . g . ( X_B - X_A )$$

<<<نتائج مهمة >>>

إن قوة الاحتكاك لا تعتبر من القوى المحافظة

الشغل المبذول من قوة غير محافظة على مسار مغلق لا يساوي الصفر

شغل القوى غير المحافظة يعتمد على المسارالذي يسلكة الجسم

علاقة الشغل بطاقة الوضع الجذبية
لدينا مكعب وزنة

Fg = m.g
يتم رفعة على مستوى مائل عديم الإحتكاك بتأثير قوة دفع إلى إرتفاع قدره
h
أعتبر أن مستوى الإختبار هو الأرض
(𝛼) زاوية ميل المستوى



$$Ug_1 = 0.0$$ $$Ug_2 = m . g . h$$ $$∆Ug = Ug_2 -Ug_1 = m . g . h$$ نحسب شغل الوزن $$W(Fg) = Fg . d. Cos 𝜃 = m . g .d .Cos 𝜃$$

من خلال قواعد الرياضيات

$$𝜃 = ( 90 + 𝛼 )$$

$$Cos 𝜃= Cos ( 90 + 𝛼 ) = - Sin ( 𝛼 )$$

$$- Sin ( 𝛼 ) = - \frac{ ℎ}{𝑑 }$$

$$d. Cos 0 = - d.\frac{ ℎ}{𝑑 } =- h$$
$$W(Fg) = Fg . d. Cos 0= - m . g . h$$ <<<نتائج مهمة >>>

$$∆Ug = - W(Fg)$$

علاقة الشغل بطاقة الوضع المرونية

طاقة الوضع المرونية : هي الطاقة التي يختزنها الجسم المرن نتيجة وضع جسيماته من بعضها البعض $$∆U_s = U_{s2} -U_{s1 }$$ $$∆U_s =\int_{{\,X_0}}^{{\,X}}-F_X.dX$$ $$∆U_s =\int_{{\,X_0}}^{{\,X}}-(-K.X).dX$$ $$∆U_s =K\int_{{\,X_0}}^{{\,X}}X.dX$$ $$∆U_s =K[\frac{X^2}{2}]_{\,X_0}^{\,X}$$ $$∆U_s =\frac{1}{2}K.X^2-\frac{1}{2}K.{X_0}^2$$

<<<نتائج مهمة >>>

$$Us = \frac{1}{2} k .X^2$$

مثال 2) نابض ثابت الصلابة له
k = 10 ( N / m )
ما مقدار الشغل اللازم حتى يستطيل بمقدار 0.4 متر

اضغط هنا تظهر طريقة الحل

طاقة الوضع والقوة

( تم الحصول على طاقة الوضع من خلال إجراء عملية تكامل سالب الشغل ( تغير القوة مضروب بتغير الازاحة
بعملية معاكسة يمكن الحصول على القوة من خلال سالب اشتقاق طاقة الوضع
$$F_X = -\frac{ d U(X) }{ d X } , F_Y = - \frac{ d U(Y) }{ d Y } , Fz = - \frac{ d U(Z }{ d Z }$$ مثال 3) الخط البياني التالي يبين العلاقة بين طاقة الوضع والموقع
عند أي موقع يكون لدينا أكبر مقدار للقوة

اضغط هنا تظهر طريقة الحل

c

<<< الطاقة الميكانيكية ومبدأ حفظ الطاقة >>>

الطاقة الميكانيكية:

في نظام مغلق إن الطاقة لا تفنى ولا تنشأ من العدم ( إلا إذا أراد الله ) ولكن تتحول من شكل إلى أخر


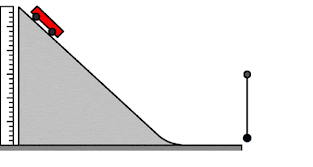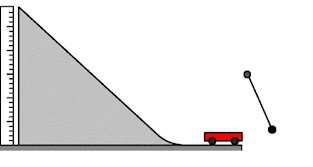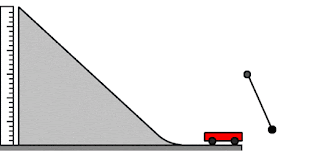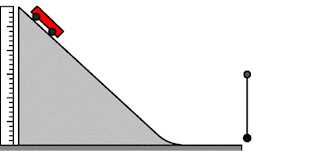
مبدأ حفظ الطاقة

على اعتبار سطح الأرض مستوى مرجعي أجب عن الأسئلة التالية.معتمد على الصورة المتحركة

مثال 1) طاقة الوضع للسيارة الحمراء تكون أعلى مايمكن عند
a)أعلى المنحدر
b)أسفل المنحدر

مثال 2) أعلى قيمة للطاقة الحركية قد اكتسبتها السيارة

a)أعلى المنحدر
b)أسفل المنحدر

اضغط هنا تظهر طريقة الحل

(الطاقة كمية قياسية )
على الرغم من أن الطاقة كمية قياسية فإن طاقة الحركة لا يمكن أن تكون سالبة أبدا


على إعتبار أن المستوى المرجعي هو عبارة عن المستوى الأفقي الذي ينزلق علية البندول حدد ما يلي
في أي موقع طاقة الحركة أكبر مايمكن $$.......................$$ أين طاقة الوضع أكبر ما يمكن $$........................$$ اين طاقة الوضع ذات قيمة سالبة $$........................$$

اضغط هنا تظهر طريقة الحل

الطاقة الميكانيكية $$M_E = K_E + GP_E$$

وهي حاصل مجموع الطاقة الحركية + طاقة الوضع :

:مبدأ حفظ الطاقة لبندول
قانون حفظ الطاقة أو بقاء الطاقة: هو قانون ينص على أنّ الطاقة في أي نظام معزول لا تفنى ولا تستحدث
( إلا إذا شاء الله ) أي أنّها لا تخلق نفسها بنفسها ولا تنتهي
ولكن يمكن تحويلها من شكلٍ إلى آخر، وتتحول الطاقة من شكل إلى آخر بالعديد من الوسائل،
حيثُ يمكن أن تتحول الطاقة الحركية إلى طاقة حرارية عن طريق الاحتكاك وتتحول طاقة الوضع إلى طاقة حركية أثناء السقوط الحر
والكثير من الأمثلة، وهكذا يمكن القول إنّ الطاقة تتبع لقوانين الانحفاظ والتي تعتبر من المبادئ الأساسية في العلوم أي أنّ الطاقة الميكانيكية لأي جسم في نظام محافظ تساوي طاقة الوضع لوحدها عندما تكون الطاقة الحركية تساوي صفراً
أو الطاقة الحركية لوحدها عندما تكون طاقة الوضع تساوي صفراً
أو مجموع كلا الطاقتين معاً
وهذا المقدار ثابت لا يتغير لهذا الجسم سواءَ كان ساكناً أم متحركاً
حيثُ يمكن أن يتغير مقدار طاقة الوضع وحده زيادةً أو نقصاناً ومقدار الطاقة الحركية زيادةً أو نقصاناً، إلّا أنّ مجموعهما يبقى ثابتاً
أي أنّ الطاقة الميكانيكية تبقى ثابتة ومحفوطة

في هذة المحاكاة
يتم التأكد من الطاقة الميكانيكية في نظام محفوظ تبقى ثابتة $$M_E=K_E+GP_E=constant$$




خيط طولة $$L=0.8 m$$ ثبت من أحد أطرافه وعلق في الطرف الأخر كتلة مقدارها $$m=0.2 kg$$ وأبعد عن موضع التوازن بزاوية مقدارها 30 درجة عن موضع الاتزان عند الموضع $$A$$ وترك ليهتز أكمل بيانات الجدول التالي معتبر أن المستوى الصفري هو موضع الاتزان

طاقةالحركة $$K_E(J)$$	طاقة الوضع $$GP_E(J)$$	الأرتفاع $$h = L - L (Cos 𝜃 )$$	الموضع
$$K_E=.........$$	$$GP_E=.........$$	$$h =.........$$	$$A$$
$$K_E=.........$$	$$GP_E=.........$$	$$h =.........$$	$$B$$
$$K_E=.........$$	$$GP_E=.........$$	$$h =.........$$	$$C$$

اضغط هنا تظهر طريقة الحل

مبدأحفظ الطاقة وحركة جسم على مستوى مائل أملس
في هذة المحاكاة يتم وضع جسمم على مستوى أملس ويترك ليتحرك يتم التحكم بوزن الجسم من خلال المنزلقة الموجود أعلى يسار التجربة
ويتم التحكم بزاوية ميل المستوى من جلال النقطة الموجودة على رأس المستوى
راقب الطاقة الحركية وطاقة الوضع والطاقة الميكانيكية أثناء إنزلاق الجسم $$M_E=K_E+GP_E=constant$$

1

وضع مكعب خشبي كتلته $$0.5\;Kg$$ على سطح مستوى أملس طولة $$1\;m$$ و يميل فوق الأفق بزاوية قدرها 20 درجة وترك المكعب لينزلق حتى نهاية المستوى المائل من خلال مبدأ حفظ الطاقة
فإن سرعة المكعب لحظة وصوله للأرض

اضغط هنا تظهر طريقة الحل

أختر الإجابة الصحيحة

---

𝜗= 5.16 m/s

---

𝜗= 2.56 m/s

---

𝜗= 1.78 m/s

---

𝜗= 3.48 m/s

---

الزنبرك
الشغل و الطاقة لقوة الزنبرك
طاقة الوضع لزنبرك تعطى بالعلاقة $$U_S=\frac {1}{2} K.X^2$$ عند تعليق جسم بزنبرك وابعاد الجسم عن موضع الاتزان يبدأ الجسم بالحركة الاهتزازية
وبشرط عدم وجود احتكاك أو مقاومة هواء
فإن الطاقة الميكانيكية تبقى ثابتة طيلة مراحل الحركة $$ME_1=ME_2$$ $$U_{S1}+KE_1= U_{S2}+KE_2$$ عند أقصى إزاحة فإن سرعة الجسم معدومة $$v=0 \Rightarrow KE=0$$ وعند أقصى إزاحة فإن الإزاحة تعادل السعة $$X=A \Rightarrow U_S=\frac {1}{2} K.A^2$$ وعند موضع الاتزان فإن الإزاحة تساوي الصفر $$X=0 \Rightarrow U_S=\frac {1}{2} K.X^2=0$$ وعند موضع الاتزان تكون سرعة الجسم أعظم ما يمكن ولحساب السرعة نطبق قانون حفظ الطاقة ونحتار موقعين أقصى إزاحة و موضع الاتزان $$ME_1=ME_2$$ $$U_{S1}+KE_1= U_{S1}+KE_1$$ $$\frac {1}{2} K.A^2 +0= 0+\frac {1}{2} m.v^2$$ $$v_{max}=\sqrt {A^2.\frac {K}{m}}=A\sqrt {\frac {K}{m}}$$ و لحساب السرعة عند أي موضع نختار موضعين عند أقصى إزاحة وعند الموضع المطلوب حساب سرعته $$ME_1=ME_2$$ $$U_{S1}+KE_1= U_{S1}+KE_1$$ $$\frac {1}{2} K.A^2 +0= \frac {1}{2} K.X^2+\frac {1}{2} m.v^2$$ $$v=\sqrt {(A^2-X^2).\frac {K}{m}}$$


القوى غير المحافظة ونظرية الشغل -الطاقة
>عند حركة جسم على مستوى خشن فإن جزء من الطاقة يستهلك في الاحتكاك
ويتحول إلى طاقة حرارية لذلك فإن
حاصل مجموع الطاقة الميكانيكية البدائية والشغل المبذول ضد قوى الأحتكاك يعادل الطاقة الميكانيكية النهائية
مبدأحفظ الطاقة وحركة جسم على مستوى مائل خشن $$kE_1 + PE_1 + W_{FK}= kE_2 + PE_2$$ في هذة المحاكاة
الطاقة الميكانيكية في حالة وجود احتكاك
عند حركة جسم على مستوى خشن فإن جزء من الطاقة يستهلك في الاحتكاك ويتحول إلى طاقة حرارية لذلك فإن حاصل مجموع الطاقة الميكانيكية البدائية والشغل المبذول ضد قوى الأحتكاك يعادل الطاقة الميكانيكية النهائية

المصدر
https://www.seilias.gr/go-lab/html5/potentialEnergy.plain.html
المصدر https://www.showmethephysics.com/home/animations3/ModphysSims.htm اكتب تعليقا واذا كان هناك خطأ اكتبه وحدد مكانه Write a comment, and if there is mistake, write and specify its location