Search

 
📄 اطبع pdf
00971504825082

<<< التيار والمقاومة >>>

التيار الكهربائي

التيار الكهربائي

التيار الكهربائي

هو عبارة عن تدفق من الشحنات الكهربائية في موصل كهربائي والشحنة الكهربية قد تكون إما إلكترونات أو أيونات
طبقًا للنظام الدولي للوحدات تقاس شدة التيار الكهربي بـوحدة الأمبير
بينما يقاس التيار الكهربي بجهاز يدعى الأميتر

في هذه المحاكاة أغلق الدائرة ولاحظ حركة الشحنات الكهربائية وكيفية فقدانها الطاقة في المقاوم

في هذه المحاكاة تمثل حركة الإلكترونات في دائرة بسيطة من الجهد الأدنى إلى الأعلى مع العلم كلمة تيار كهربائي تعني حركة شحنات موجبة من الجهد الأعلى إلى الجهد الأدنى

رسم توضيحي للتيار الكهربائي

كثافة التيار الكهربائي

هو عبارة عن التيار المتدفق خلال وحدة المساحة في سلك موصل عند نقطة معينة
يرمز لكثافة التيار بالرمز j
وهو كمية متجهه اتجاهه باتجاه حركة الشحنات الموجبة (عكس حركة الالكترونات)

\[j=\frac{i}{A}\] وتقدر بوحدة قياس \[\frac{A}{m^2}\]

سرعة الانسياق وهي سرعة الالكترونات الموجهة في الدائرة الكهربائية
أي سلك موصل يحتوي على الكترونات تتحرك بشكل عشوائي وبسرعة عالية عند تطبيق فرق في الجهد بين طرفي السلك تصبح حركة الالكترونات سرعة عشوائية موجهه تدعى سرعة الانسياق وتكون السرعة بطيئة جدا من رتبة \[𝜗_d =10^{-4}\frac {m}{s}\]

رسم توضيحي لسرعة الانسياق

(A) لدينا موصل مساحة مقطعه
(𝜗𝑑) وطبق علية مجال كهربائي تتحرك الالكترونات عكس المجال بسرعة انسياق
(d t) وخلال فترة زمنية قدرها
تقطع مسافة قدرها \[𝜗𝑑 . dt\] وبالتالي حجم الالكترونات التي تمر عبر المقطع تعادل
\[A. 𝜗𝑑 . dt\] فيكون عدد الالكترونات في هذا الحجم تعادل
\[n . A. 𝜗𝑑 . dt\]
(-e) وكل إلكترون مشحون بشحنة مقدارها
إذا الشحنة المتدفقة عبر هذه المساحة
\[dq = - e. n . A. 𝜗𝑑 . dt\]

فنحصل على شدة التيار
\[i =\frac{ dq }{ dt }= - e. n . A. 𝜗𝑑\]

وكثافة التيار
\[j = \frac{i}{A} = - e. n . 𝜗𝑑\]

فاصل
\[1 \star\]

سلك مساحة مقطعه \[A=5.2×10^{-6}m^2\] ويمر به تيار شدته \[i=2\;A\] ومصنوع من النحاس كتلته المولية وكثافتة \[M=63.5\;\; g\;\;\;\;\;\;.𝜌=8960 \frac{Kg}{m^3}\] ويوجد الكترون موصل واحد في كل ذره ، فإن سرعة الانسياق للإلكترونات تعادل علما بأن \[ q=1.6 ×10^{-19}c\;\;\;\;\;\;Avogadro's\;\; number= 6.022 ×10^{23}\]

اختر الإجابة الصحيحة

\[𝑣_𝑑= 6×𝟏𝟎^{−5}\;\; m/s\]
A
\[𝑣_𝑑= 2.8×𝟏𝟎^{−4}\;\; m/s\]
B
\[𝑣_𝑑= 5.6×𝟏𝟎^{−4}\;\; m/s\]
C
\[𝑣_𝑑= 4.3×𝟏𝟎^{−5}\;\; m/s\]
D
فاصل

قانون أوم

في هذه المحاكاة درس العالم أوم العلاقة بين شدة التيار وفرق الجهد بين طرفي مقاوم أومي لذلك أختر قيمة لمقاومة أومية وقم بتغير فرق الجهد في كل مرة لاحظ ماذا يحدث لشدة التيار كرر التجربة مع مقاومة أخرى

تجربة قانون أوم أكمل بيانات الجدول التالي

رقم التجربة فرق الجهد (فولت) شدة التيار (أمبير) المقاومة (أوم)
1
2
3
4
5

قانون أوم

قانون أوم هو مبدأ أساسي في الكهرباء، أطلق عليه هذا الاسم نسبة إلى واضعه الفيزيائي الألماني "جورج سيمون أوم". وينص على أن فرق الجهد الكهربائي بين طرفي ناقل معدني يتناسب طرديا مع شدة التيار الكهربائي المار فيه.

يتم تعريف النسبة الثابتة بين فرق الجهد وشدة التيار بالمقاومة الكهربائية ويلاحظ أن المقاومة لناقل ما، هي قيمة ثابتة ولا تتغير بتغير فرق الجهد بين طرفيه،

يمكن التعبير عن المعادلة بصيغة التالية
\[ V = I . R \]

قيم نفسك

فاصل

المقاومة النوعية والمقاومة

المقاومة الكهربائية :وهي مدى ممانعة المادة لمرور التيار الكهربائي
عند تطبيق فرق جهد بين طرفي سلك \[∆V\] ويمر به تيار شدته \[i\] فإن ممانعة السلك لمرور التيار تعطى بالعلاقة حسب قانون أوم \[R=\frac {∆V}{i}\] وحدة قياس المقاومه الكهربائية هي أوم وهي تعادل \[𝝮=\frac{V}{A}\]

توصف بعض الأجهزة من حيث مقدرتها على التوصيل وليس بمقدرتها على ممانعة التيار
\[G\] وهي تقدر بوجدة السيمنس \[G=\frac {i}{∆V}=\frac {1}{R}\;\;\;\;\;\;\;\;\;\;\;\;\;\;S=\frac {A}{V}=\frac {1}{𝝮}\]

أن ممانعة أي سلك لمرور التيار تعتمد على المادة المصنوع منها السلك والشكل الهندسي له ودرجة الحرارة
ولكل سلك مقاومة خاصة به تدعى المقاومة النوعية \[𝜌\] وهي عبارة عن النسبة بين شدة المجال الكهربائي إلى كثافة التيار
\[𝜌=\frac {E}{J}\;\;\;\;\;\;\;\;\;\;\;𝜌=\frac {\frac {V}{m}}{\frac {A}{m^2}}=\frac {V.m}{A}=𝝮.m\]

المقاومة النوعية ومعامل درجة الحرارة للمقاومة النوعية لبعض الموصلات

\[∝\] معامل درجة الحرارارة عند الدرجة حرارة \[20^0c\] \[×10^{-3}\;\;K^{-1}\]

\[ 𝜌\] المقاومة النوعية عند درجة حرارة \[20^0c\] \[×10^{-8}\;\;𝝮.m\]

اسم المادة

3.8

1.6

الفضة

3.9

1.72

النحاس

3.4

2.44

الذهب

3.9

2.82

الالمنيوم

2

3.9

النحاس الأصفر

4.5

5.51

التنجستن

5

9.7

الحديد

نحن نعلم أن
\[E=\frac{∆V}{L}\;\;\;\;\;\;\;\;\;J=\frac{i}{A}\]
\[𝜌=\frac {E}{J}=\frac {\frac{∆V}{L}}{\frac{i}{A}}=\frac{∆V.A}{i.L}=\frac{iR.A}{i.L}=\frac{R.A}{L}\]
\[R= 𝜌.\frac{A}{L}\]

العوامل المؤثرة على المقاومة الأومية

في هذه المحاكاة نلاحظ قيمة المقاومة تتغير بتغير طول المقاوم ومساحة المقطع ونوع المادة المصنوع منها المقاوم

\[2 \star\]

اربع أسلاك من نفس النوع وبنفس درجة الحرارة أحد الاسلاك التالية لها أقل مقاومة

اختر الإجابة الصحيحة

سلك 1
A
سلك 2
B
سلك 3
C
سلك 4
D
\[3 \star\]

سلكان من نفس المادة وبنفس درجة الحرارة فإذا كانت \[\frac{R_1}{R_2}= \frac{2}{3}\] فإن أحد الإجابات التالية تحقق ذلك

اختر الإجابة الصحيحة

\[L_1=\frac{3}{4}L_2 , A_1=\frac{1}{2} A_2\]
A
\[L_1=\frac{4}{3}L_2 , A_1=2 A_2\]
B
\[L_1=\frac{1}{2}L_2 , A_1=\frac{1}{3} A_2\]
C
\[L_1=3L_2 , A_1=2 A_2\]
D
  • اضغط هنا تظهر طريقة الحل
    • هناك عامل أخر وهو درجة الحرارة نلاحظ أثر ارتفاع درجة الحرارة على المقاومة النوعية


    \[ρ_T= ρ_0[1 +𝛼 (T–T_0)]\]\[R_T= R_0[1 + 𝛼 (T–T_0)]\]
    \[4 \star\]

    سلك من النحاس مقاومته النوعية
    \[1.7 \times 10^{-8} \;Ω.m\] في درجة حرارة 20 درجة سيليزية تم رفع درجة الحرارة بما يعادل 15 درجة سيليزية فأصبحت مقاومته النوعية \[1.82 \times 10^{-8} \;Ω.m\] فإن معامل التغير في درجة الحرارة يعادل

    اختر الإجابة الصحيحة

    A
    \[𝛼=21.7 × 10^{-3}\;K^{-1}\]
    B
    \[𝛼=2.6 × 10^{-3}\;K^{-1}\]
    C
    \[𝛼=5.6 × 10^{-3}\;K^{-1}\]
    D
    \[𝛼=4.7 × 10^{-3}\;K^{-1}\]
    اضغط هنا تظهر طريقة الحل

    رموز ومفتاح خطوط المقاومات :( أربع خطوط ) قراءة المقاومات من خلال الخطوط الملونة يمكن أن يحتوي المقاوم المكون من الكربون على 4 إلى 6 خطوط يمثل الخط الأول هو العشرات والخط الثاني هو الاحاد لقيمة المقاومة أما الخط الثالث يمثل قوة مرفوع إلى الرقم 10 أما الخط الرابع يمثل نسبة الخطأ في القراءة



    القوة الدافعة الكهربائية

    البطارية: تبذل شغلًا على الشحنات الكهربائية في الدائرة وتعطيها طاقة كهربائية وتدفعها في الدائرة لذلك تدعى القوة الدافعة الكهربائية.

    تمثيل التيار والجهد الكهربائي

    عند وصل البطارية في دائرة تحتوي على أسلاك موصلة يتكون مجال كهربائي يعمل على إعطاء طاقة للشحنات الخارجة منها التي تصطدم مع الشحنات الموجودة في الأسلاك الموصلة وتوجه حركتها وتدفعها في أجزاء الدائرة.

    البطارية تبذل قوة على الشحنات \[f\] وتعطيها طاقة كهربائية \[e\] وتدفعها وتحركها في الدائرة \[m\] لذلك يرمز لفرق الجهد الناتج عن البطارية:

    \[V_{emf}\]

    مثال 1) البطارية توفر فرق جهد ذا قيمة ثابتة بينما لا توفر تيارًا ثابتًا. ما هو السبب؟

    مثال 1
    اضغط هنا تظهر طريقة الحل

    مثال 2) بطارية قابلة للشحن كتب عليها \[ 2500 mAh\] ما مقدار الشحنة التي توفرها؟

    مثال 2
    اضغط هنا تظهر طريقة الحل

    قام أحد الطلاب بقياس فرق الجهد بين طرفي بطارية:

    - والدائرة مفتوحة

    - ومرة ثانية والدائرة مغلقة

    فكانت القياسات الموضحة بالشكل:

    قياسات الجهد

    لتحديد السبب أجري التجربة التالية: هناك دائرتين إحداهما مغلقة والثانية مفتوحة.





    قارن بين قراءة جهاز الفولتميتر لكلا الدائرتين. إن الدائرة المغلقة حدث بها ضياع في جهد المصدر. السبب في ذلك يوجد داخل البطارية مقاومة تدعى المقاومة الداخلية يرمز لها بالرمز (r) وتقدر بوحدة أوم (Ω).

    قم بحساب قيمة المقاومة الداخلية للبطارية من خلال الجهد الذي فقد وقيمة التيار المار في الدائرة:

    r = Vr / I

    المقاومة الداخلية

    عند قياس فرق الجهد بين طرفي البطارية والدائرة مفتوحة يدعى القوة المحركة الدافعة \[(emf).\]

    لم تظهر قيمة المقاومة الداخلية إلا إذا مر تيار بها. أما عند القياس والدائرة مغلقة فهذا يدعى فرق الجهد وهو أصغر دائمًا من القوة المحركة الدافعة.

    مقارنة بين emf وفرق الجهد

    إذا أهملت المقاومة الداخلية، عندها تعادل القوة المحركة الدافعة فرق الجهد.

    مثال 3) في الشكل المقاومة الخارجية 10 أوم والمقاومة الداخلية للبطارية 2 أوم. عند إغلاق الدائرة حدد قيم البيانات التالية:

    مثال 3

    الجهد المصروف بين طرفي المقاومة الخارجية 10 أوم يعادل:

    VR = ....................

    الجهد المصروف بين طرفي المقاومة الداخلية 2 أوم يعادل:

    Vr = ....................

    القوة المحركة للبطارية تعادل:

    Vemf = ....................

    اضغط هنا تظهر طريقة الحل
    \[5 \star \star\]

    دائرة متصلة بمقاوم \[4 Ω\] ومفتاح. يتم توصيل الفولتميتر عبر الدائرة يقرأ عندما يكون المفتاح مفتوحًا \[12V\] وعندما يكون المفتاح مغلقا \[10V\]
    فإن قيمة المقاومة الداخلية للبطارية تعادل

    رسم توضيحي للدائرة الكهربائية
    A
    \[𝑟= 0.5\;\; Ω\]
    B
    \[𝑟= 1\;\; Ω\]
    C
    \[𝑟= 0.8\;\; Ω\]
    D
    \[𝑟= 1.2\;\; Ω\]
  • طريقة الحل اضغط هنا تظهر طريقة الحل



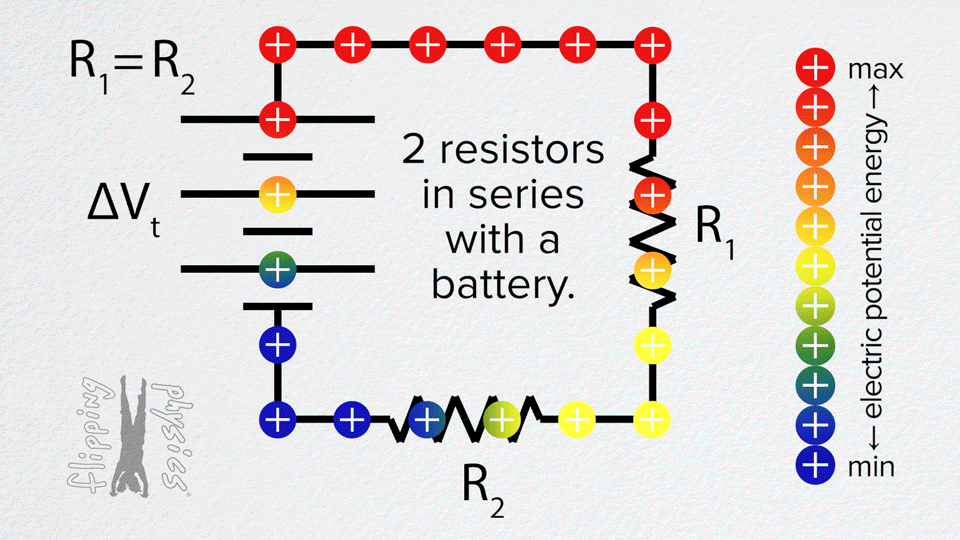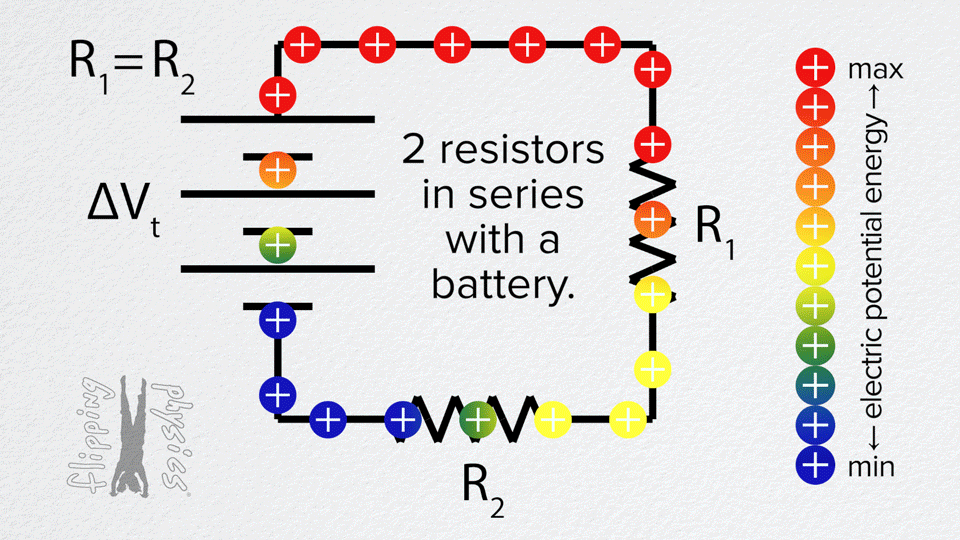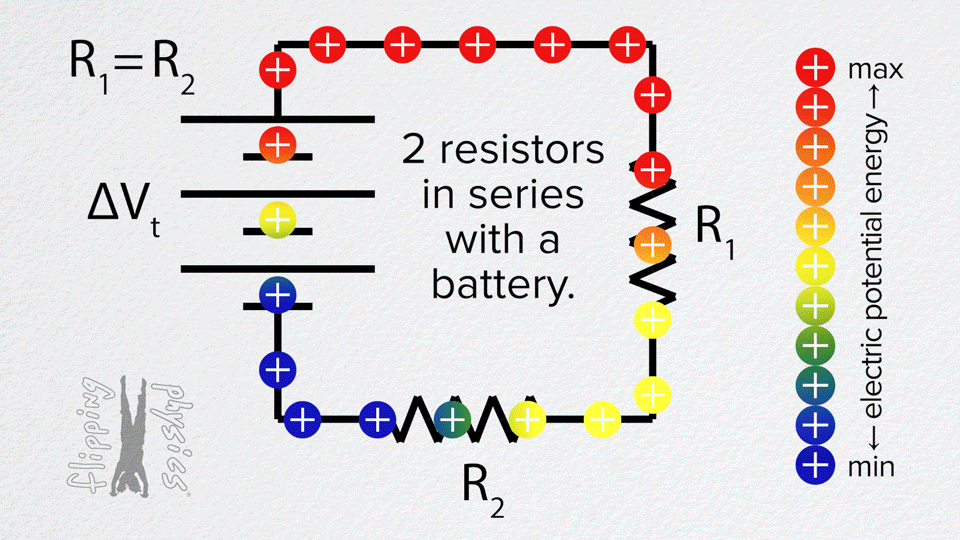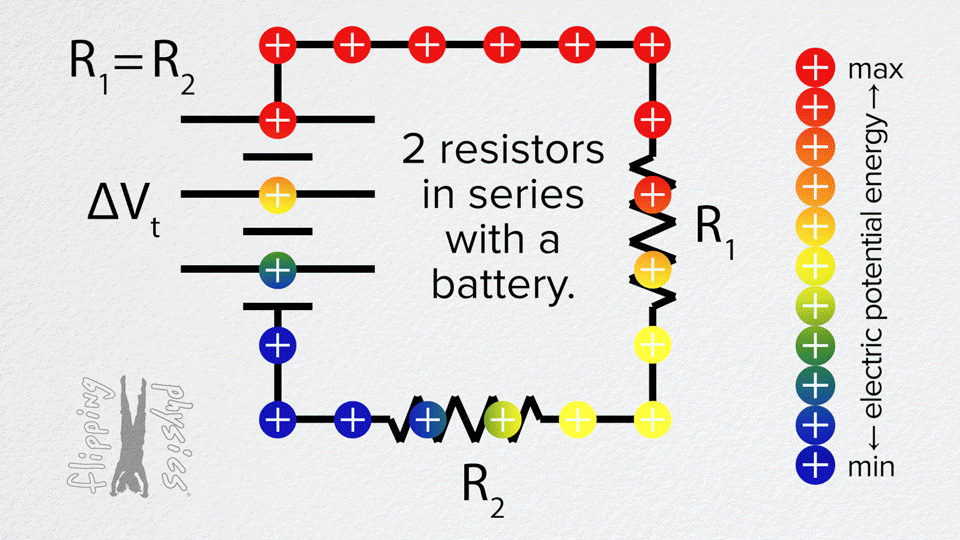
    • توصيل المقاومات على التوالي
    التوصيل على التوالي يسير التيار الكهربائي في مسار واحد ويمر بجميع مكونات الدارة

    التوصيل على التوالي يكون مقدار التيار المار في كل مكون من مكونات الدارة متساوياً والجهد للمصدر يتوزع على المقاومات وترتفع قيمة المقاومة المكافئة

    في هذه المحاكاة وصل ثلاث مقاومات على التوالي وقم بقياس شدة التيار الكلي وشدة التيار المار في كل مقاوم وايضا قم بقياس قرق الجهد الكلي وفرق الجهد بين طرفي كل مقاوم سجل النتائج

    تجربة : دائرة المقاومات على التوالي

    تعليمات:

    1. قم بإدخال قيم المقاومات (R1, R2, R3) في الحقول المخصصة

    2. أدخل قيمة الجهد الكلي (V_tot) أو التيار الكلي (I_tot)

    3. قم بحساب القيم الأخرى بناءً على قوانين دوائر التوالي

    4. اضغط على زر "تصحيح الإجابات" للتحقق من صحة إجاباتك

    \[R_{eq}\]=?Ω \[R_{3}\]= Ω \[R_{2}\]= Ω \[R_{1}\]= Ω
    \[I_{tot}\]=A \[I_{3}\]=A \[I_{2}\]=A \[I_{1}=\]A
    \[V_{tot}\]=V\] \[V_{3}\]=V \[V_{2}\]=V \[V_{1}\]=V
    \[R_{eq} = \frac{V_{tot}}{I_{tot}}\]
    \[R_{eq}\] = ........    		 \[R_{eq} = R_1 + R_2 + R_3\]
    \[R_{eq} \]= ........    		 ماذا تستنتج في التيار المار في المقاومات
    		 ماذا تستنتج في فرق الجهد بين طرفي كل مقاوم

    ميزات التوصيل على التوالي :

    نتائج مهمة




    التيارثابت في جميع المقاومات ويعادل التيار الكلي

    \[I_{total} = I_1=I_2=I_3 \]

    الجهد يتوزع على المقاومات والمقاوم الأكبر يأخذ الجهد الأكبر

    \[ V_{total} = V_1+V_2+V_3 \]

    المقاومة المكافئة يساوي حاصل مجموع المقاومات

    \[R_{eq}= R_1+R_2+R_3)=\frac{ V_{total}}{ I_{total }}\]







    \[6 \star\]

    ثلاث مقاومات على التوالي \[ R_1 = 10 Ω , R_2 = 5 Ω , R_3 = ? \] تم توصيلهم ببطارية فرق جهدها \[V= 20 V\] مر تيار شدتة \[I=0.5 A\] فإن قيمة المقاوم \[ R_3 =....\]

    اختر الإجابة الصحيحة

    \[R_3=12\;Ω\]
    A
    \[R_3=25\;Ω\]
    B
    \[R_3=15\;Ω\]
    C
    \[R_3=20\;Ω\]
    D
  • اضغط هنا تظهر طريقة الحل
    • \[7 \star\]

    في الدائرة أدناه قراءة جهاز الاميتر تعادل

    اختر الإجابة الصحيحة

    A
    \[I=1.11\;A\]
    B
    \[I=2.22\;A\]
    C
    \[I=3.33\;A\]
    D
    \[I=4.44\;A\]
  • اضغط هنا تظهر طريقة الحل


    • توصيل المقاومات على التوازي
    التوصيل على التوازي عندما يسير التيار الكهربائي بأكثر من مسار واحد ويمر بجميع مكونات الدارة

    في حالة التوصيل على التوازي يتوزع التيار المار في مكونات الدارة كلا حسب مقاومتة والجهد للمصدر يعادل الجهد لكل فرع من أفرع التوازي

    في هذه المحاكاة وصل ثلاث مقاومات على التوازي وقم بقياس شدة التيار الكلي وشدة التيار المار في كل مقاوم وايضا قم بقياس قرق الجهد الكلي وفرق الجهد بين طرفي كل مقاوم سجل النتائج في الجدول االموجود أسفل التجربة


    تجربة : دائرة المقاومات على التوازي

    تعليمات:

    1. قم بإدخال قيم المقاومات (R1, R2, R3) في الحقول المخصصة

    2. أدخل قيمة الجهد الكلي (V_tot)

    3. قم بحساب القيم الأخرى بناءً على قوانين دوائر التوازي

    4. اضغط على زر "تصحيح الإجابات" للتحقق من صحة إجاباتك

    \[R_{eq}\]=?Ω \[R_{3}\]= Ω \[R_{2}\]= Ω \[R_{1}\]= Ω
    \[I_{tot}\]=A\] \[I_{3}\]=A \[I_{2}\]=A \[I_{1}\]=A
    \[V_{tot}\]=V\] \[V_{3}\]=V \[V_{2}\]=V \[V_{1}\]=V
    \[R_{eq} = \frac{V_{tot}}{I_{tot}}\]
    \[R_{eq} \]= ........    		 \[\frac{1}{R_{eq}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}\]
    \[R_{eq}\] = ........    		 ماذا تستنتج في التيار المار في المقاومات
    		 ماذا تستنتج في فرق الجهد بين طرفي كل مقاوم

    التوصيل على التوازي :يسير التيار الكهربائي ضمن أكثر من مسار واحد حتى يكمل دورته
    ميزات التوصيل على التوازي :

    نتائج مهمة




    التيار يتوزع على المقاومات المقاوم الأكبر يمر به تيار أقل

    \[I_{total} = I_1+I_2+I_3 \]

    الجهد متساوي ويعادل جهد المصدر

    \[ V_{total} = V_1=V_2=V_3 \]

    مقلوب لمقاومة المكافئة يساوي حاصل مجموع مقاوب المقاومات

    \[R_{eq}=(\frac{1}{ R_1}+\frac{1}{R_2}+\frac{1}{R_3})^{-1}=\frac{ V_{total}}{ I_{total }}\]





    في هذه المحاكاة دائرة يتم قياس شدة التيار وفرق الجهد في كل مقاوم من خلال جهاز الأميتر والفولتميتر
    يمكن أن نغير مقدار المقاومات من خلال الايقونة الموجودة أسفل كل مقاوم


    \[8 \star\]

    ثلاث مقاومات على التوازي \[ R_1 = 3 Ω , R_2 = 9 Ω , R_3 = ? \] تم توصيلهم ببطارية فرق جهدها \[V= 10 V \] فمر تيار كلي شدتة \[I= 5 A\] فإن قيمة المقاوم \[ R3 =.....\]
    A
    \[ 10 Ω \]
    B
    \[ 18 Ω \]
    C
    \[ 12Ω \]
    D
    \[ 20 Ω \]
  • اضغط هنا تظهر طريقة الحل
    • \[9 \star\]

    في الدائرة المجاورة قراءة جهاز الاميتر للتيار الكلي تعادل
    A
    \[ 3 A \]
    B
    \[ 6 A \]
    C
    \[ 9 A \]
    D
    \[ 2 A \]
  • اضغط هنا تظهر طريقة الحل
    • \[10 \star\]

    مقاومان الأول \[R_1=50 Ω\] والثاني مجهول المقاومة تم توصيلهما فكانت المقاومة المكافئة \[R_{eq}=80 Ω\] التوصيل كان
    A
    على التوالي
    B
    على التوازي
  • اضغط هنا تظهر طريقة الحل
    • \[11 \star\]

    مقاومان متساويان تم توصيلهم لوحظ أن فرق الجهد للأول يساوي فرق الجهد للثاني ويعادل مجموع جهد المقاومان جهد المصدر فإن التوصيل كان
    A
    على التوالي
    B
    على التوازي
  • اضغط هنا تظهر طريقة الحل





    • الدوائر الكهربائية المركبة



    خطوات حساب المقاومة المكافئة لدائرة
    نحدد من هي المقاومات على التوالي ومن على التوازي




    مثال 1 ) مجموعة من المقاومات متصلة كما في الشكل والبطارية تحتوي على مقاومة داخلية أوجد المقاومة المكافئة


  • اضغط هنا تظهر طريقة الحل



    • في هذه المحاكاة مجموعة من المقاومات متصلة على التوالي والتوازي نستطيع التحكم بمقاديرها ويتم إضهار قيمة التيار وفرق الجهد في كل مقاوم




    مثال 2 ) مجموعة من المقاومات متصلة كما في الشكل فإن شدة التيار المار في المقاوم

    R1 = ?


  • اضغط هنا تظهر طريقة الحل

    • مثال 3 ) مجموعة من المقاومات متصلة كما في الشكل فإن فرق الجهد بين طرفي المقاوم

    R4 = ?

  • اضغط هنا تظهر طريقة الحل




    • الطاقة والقدرة

    عند تطبيق فرق جهد في دائرة فإن القوة المحركة الكهربائية للبطارية تعمل على بذل شغل على الشحنات وتعطيها طاقة كهربائية
    \[ dU = dq . ∆𝑉 \]
    ونحن نعلم أن
    \[dq = I . dt\]
    \[dU = I . dt .∆𝑉 \]
    \[\frac{𝑑𝑈}{dt}\] وهي معدل الطاقة الصروفة وتدعى القدرة ويرمز لها بالرمز \[P\] \[P = I . ∆𝑉\]
    وتقدر بوحدة الوات في النظام الدولي
    وحسب قانون أوم \[R = \frac{∆𝑉}{I}\] يمكن كتابة القدرة \[𝑃= I^2. 𝑅\]\[𝑃= \frac{∆𝑉^2}{𝑅}\]



    في هذة المحاكاة دائرة تحتوي على مقاومة أومية تعمل على استهلاك طاقة البطارية




    القدرة المصروفة في دائرة مقاومات على التوالي




    القدرة المصروفة في دائرة مقاومات على التوازي




    القدرة المصروفة في دائرة مقاومات على التوالي و التوازي




    \[12 \star \star\]

    تتكون الدائرة المبسطة، من بطارية 9 فولت بدون مقاومة داخلية وثلاث مقاومات كما هو موضح في الشكل أدناه. فإن القدرة الكلية للدائرة تعادل

    اختر الإجابة الصحيحة

    A
    \[P=13.75\;\;W\]
    B
    \[P=20.25 \;\;W\]
    C
    \[P=25.45\;\;W\]
    D
    \[P=17.85\;\;W\]
    اضغط هنا تظهر طريقة الحل


    سطوع المصابيح
    عندما نتكلم عن سطوع المصابيح علينا أن نبحث عن القدرة كلما كانت قدرة المصباح أكبر كان سطوعه أكبر \[P = V.I = I^2.R =\frac{V^2}{R}\] \[P=\frac{W}{t}\]


    هذه محاكاة عدة مصابيح متصلة ببعضها البعض قارن بين سطوع هذه المصابيح


    هذه محاكاة لدائرة مركبة مع مصدر طاقة وأربعة مصابيح كهربائية متطابقة وثلاثة مفاتيح. افتح المفاتيح وأغلقها وقم بعمل تنبؤات حول كميات الجهد عبر المصابيح ، والتيارات عبر المصابيح ، وسطوع المصابيح (التي ترتبط بالطاقة التي يتبدد كل منها كحرارة وضوء). استخدم مربعات الاختيار لإظهار الفولتية والتيارات أو إخفائها.



    \[13 \star\]

    في الدائرة المجاورة تم وصل 4 مصابيح كما في الشكل أحد الإجابات التالية تحقق انخفاض في قراءة الاميتر الموجود في الدائرة

    اختر الإجابة الصحيحة

    (A) وصل سلك بين طرفي المصباح -A
    A
    (B) احترق فتيل المصباح -B
    B
    (C) وصل سلك بين طرفي المصباح -C
    C
    (D) وصل سلك بين طرفي المصباح -D
    D
    اضغط هنا تظهر طريقة الحل
    \[14 \star\]

    في الشكل المجاور 4 مصابيح متماثله في المقاومة وصلت ببطارية أحد المصابيح التالية لها أشد سطوع

    اختر الإجابة الصحيحة

    المصباح A
    A
    المصباح B
    B
    المصباح C
    C
    المصباح D
    D
    اضغط هنا تظهر طريقة الحل
    \[15 \star\]

    في الشكل إدناه القدرة المبددة في الدائرة تعادل

    اختر الإجابة الصحيحة

    \[P=54\;\; W\;\;\;\;\;\;-A\]
    A
    \[P=97\;\; W\;\;\;\;\;\;-B\]
    B
    \[P=69\;\; W\;\;\;\;\;\;-C\]
    C
    \[P=88\;\; W\;\;\;\;\;\;-D\]
    D
    اضغط هنا تظهر طريقة الحل
    \[16 \star\]

    مصباح كتب عليه (60W, 220V) فإن مقاومة المصباح والطاقة المستهلكة خلال 10 minutes

    اختر الإجابة الصحيحة

    \[R=504.6 Ω , E=25000 J \;\;\;\;\;\;-A\]
    A
    \[R=807.6 Ω , E=36000 J;\;\;\;\;\;-B\]
    B
    \[ R=954.4 Ω , E=13244 J\;\;\;\;\;\;-C\]
    C
    \[R=650.8 Ω , E=16860 J \;\;\;\;\;\;-D\]
    D
    اضغط هنا تظهر طريقة الحل

    اكتب تعليقا واذا كان هناك خطأ اكتبه وحدد مكانه Write a comment, and if there is mistake, write and specify its location

    5 comments:

    🧮 Calculator
    🗑️
    ✏️ قلم