📄 اطبع pdf
00971504825082
قانون كولوم
قانون كولوم
العوامل المؤثرة على القوة الكهربائية بين شحنتين
قانون كولوم:
\[F=K.\frac{q_1.q_2}{r^2}\]
العوامل الرئيسية:
-
مقدار الشحنتين (q₁ و q₂):
العلاقة طردية مع حاصل ضرب الشحنتين
مثال: إذا تضاعفت إحدى الشحنتي
→ تتضاعف القوة
-
المسافة بينهما (r):
العلاقة عكسية مع مربع المسافة
مثال: إذا زادت المسافة الضعف
→ تقل القوة إلى الربع
-
الوسط المادي (k):
ثابت العزل الكهربائي يعتمد على الوسط:
k = 1/(4πε₀εᵣ)
حيث εᵣ هي السماحية النسبية للوسط
العلاقة الرياضية:
- \[F ∝ q₁q₂ \](طردية)
- \[F ∝\frac { 1}{r²} \](عكسية تربيعية)
- \[F ∝ \frac {1}{εᵣ }\](عكسية مع سماحية الوسط)
القوة الكهربائية بين شحنتين
قانون كولوم
القوة الكهربائية بين شحنتين نقطيتين تتناسب طرديًا مع حاصل ضرب مقدار الشحنتين وعكسيًا مع مربع المسافة بينهما :
\[F=K.\frac{q_1.q_2}{r^2}\]
حيث:
k = ثابت كولوم ≈ 8.9875×10⁹ N·m²/C²
أنواع القوى الكهربائية
1. قوة تجاذب
تحدث عندما تكون الشحنتان مختلفتين في النوع (واحدة موجبة والأخرى سالبة)
مثال: تجاذب الإلكترونات للنواة في الذرة
2. قوة تنافر
تحدث عندما تكون الشحنتان متشابهتين في النوع (كلتاهما موجبتان أو سالبتان)
مثال: تنافر شحنتين على بالونين مشحونين بنفس النوع
خصائص هامة
- قوة متبادلة (تساوي في المقدار وتعاكس في الاتجاه)
- قوة مركزية (تقع على الخط الواصل بين الشحنتين)
- تقل شدتها بزيادة المسافة بين الشحنتين
- تعتمد على الوسط العازل بين الشحنتين
تطبيقات عملية
- تصميم الدوائر الإلكترونية
- عمل المكثفات الكهربائية
- ظاهرة البرق
- الطابعات الليزرية
ملاحظات هامة:
1. القوة تنافرية إذا كانت الشحنتين متشابهتين
2. القوة تجاذبية إذا كانت الشحنتين مختلفتين
3. وحدة القوة: نيوتن (N)
4. التأثير المتبادل وفق قانون نيوتن الثالث
القوة الكهربائية بين ثلاث شحنات على خط مستقيم
قانون كولوم:
القوة بين شحنتين:
\[F=K.\frac{q_1.q_2}{r^2}\]
آلية تحديد القوة المحصلة:
- حدد اتجاه القوة بين كل زوج (تنافر ←← أو تجاذب →←)
- احسب مقدار القوة بين كل زوج باستخدام القانون
- اجمع القوى بشكل متجهي حسب اتجاهها
جدول تحديد الاتجاه (للشحنة الوسطى):
ترتيب الشحنات
اتجاه القوة
مثال
(+ , + , +)
← إذا كانت أقرب لليسار، → إذا أقرب لليمين
Q1=+2C, Q2=+3C, Q3=+5C
(- , - , -)
→ إذا كانت أقرب لليسار، ← إذا أقرب لليمين
Q1=-4C, Q2=-1C, Q3=-3C
(+ , + , -)
← من اليسار (تنافر)، → من اليمين (تجاذب)
Q1=+5C, Q2=+2C, Q3=-6C
(- , + , +)
→ من اليسار (تجاذب)، ← من اليمين (تنافر)
Q1=-3C, Q2=+4C, Q3=+1C
ملاحظات:
- علامة الشحنة تحدد نوع القوة (تنافر/تجاذب)
- المسافة بين الشحنات تحدد شدة القوة
- اتجاه القوة المحصلة يُحدد بمقارنة شدتي القوتين
تحليل القوى الكهربائية في مثلث قائم
التركيب الهندسي:
ثلاث شحنات نقطية (q₁، q₂، q₃) موضوعة على:
- q₁ و q₂ عند الضلعين القصيرين
- q₃ عند الرأس القائم (الزاوية 90°)
قانون كولوم الأساسي:
\[F=K.\frac{q_1.q_2}{r^2}\]
حيث kₑ = 8.99×10⁹ N·m²/C²
خطوات حساب المحصلة على q₃:
- احسب القوة بين q₁ و q₃ \[F_{12}=K.\frac{q_1.q_2}{a^2}\]
- احسب القوة بين q₂ و q₃: \[F_{23}=K.\frac{q_2.q_3}{b^2}\]
- حلل القوى إلى مركبات:
- F₁₃ → مركبة أفقية (F₁₃x) ومركبة رأسية (F₁₃y)
- F₂₃ → مركبة أفقية (F₂₃x) ومركبة رأسية (F₂₃y)
- المحصلة الكلية:
\[Fₜₒₜₐₗ_x = ΣFₓ\]
\[Fₜₒₜₐₗ_y = ΣFᵧ\]
تحديد اتجاه المحصلة:
\[ θ = tan^{-1}\frac {(Fₜₒₜₐₗ_y )}{ (Fₜₒₜₐₗ_x)}\]
ملاحظات هامة:
- تأخذ إشارة الشحنات في الاعتبار (تجاذب/تنافر)
- المسافات تُحسب باستخدام نظرية فيثاغورث إذا لزم الأمر
- الاتجاه يعتمد على طبيعة الشحنات:
نوع الشحنات
اتجاه القوة
متماثلة
تنافر
مختلفة
تجاذب
القوة بين شحنتين
ثلاث شحنات على خط مستقيم
مثلث قائم الزاوية
القوة الكهربائية المحصلة
اختبار قانون كولوم والقوة الكهربائية
\[1 \star\]
\[2 \star\]
\[3 \star\]
\[4 \star\]
\[5 \star\]
\[6 \star\]
\[7 \star\]
نتيجة الاختبار
لقد أجبت على 0 من أصل 7 أسئلة بشكل صحيح
Coulomb's Law
Coulomb's Law
Factors Affecting the Electric Force Between Two Charges
Coulomb's Law:
\[F=K.\frac{q_1.q_2}{r^2}\]
Main Factors:
-
Magnitude of the Charges (q₁ and q₂):
Directly proportional to the product of the charges
Example: If one charge doubles
→ The force doubles
-
Distance Between Them (r):
Inversely proportional to the square of the distance
Example: If the distance doubles
→ The force decreases to one-fourth
-
Medium (k):
Dielectric constant depends on the medium:
k = 1/(4πε₀εᵣ)
where εᵣ is the relative permittivity of the medium
Mathematical Relationships:
- \[F ∝ q₁q₂ \](Direct)
- \[F ∝\frac { 1}{r²} \](Inverse square)
- \[F ∝ \frac {1}{εᵣ }\](Inverse with medium permittivity)
Electric Force Between Two Charges
Coulomb's Law
The electric force between two point charges is directly proportional to the product of the charges and inversely proportional to the square of the distance between them:
\[F=K.\frac{q_1.q_2}{r^2}\]
Where:
k = Coulomb's constant ≈ 8.9875×10⁹ N·m²/C²
Types of Electric Forces
1. Attractive Force
Occurs when the charges are of opposite types (one positive and one negative)
Example: Attraction between electrons and nucleus in an atom
2. Repulsive Force
Occurs when the charges are of the same type (both positive or both negative)
Example: Repulsion between two similarly charged balloons
Important Properties
- Mutual force (equal in magnitude and opposite in direction)
- Central force (acts along the line joining the charges)
- Decreases with increasing distance between charges
- Depends on the insulating medium between charges
Practical Applications
- Design of electronic circuits
- Operation of capacitors
- Lightning phenomenon
- Laser printers
Important Notes:
1. Force is repulsive if charges are similar
2. Force is attractive if charges are different
3. Unit of force: Newton (N)
4. Mutual interaction according to Newton's third law
Electric Force Between Three Charges in a Straight Line
Coulomb's Law:
Force between two charges:
\[F=K.\frac{q_1.q_2}{r^2}\]
Method for Determining Resultant Force:
- Determine direction of force between each pair (repulsion ←← or attraction →←)
- Calculate magnitude of force between each pair using the law
- Add forces vectorially according to their direction
Direction Determination Table (for the middle charge):
Charge Arrangement
Force Direction
Example
(+ , + , +)
← if closer to left, → if closer to right
Q1=+2C, Q2=+3C, Q3=+5C
(- , - , -)
→ if closer to left, ← if closer to right
Q1=-4C, Q2=-1C, Q3=-3C
(+ , + , -)
← from left (repulsion), → from right (attraction)
Q1=+5C, Q2=+2C, Q3=-6C
(- , + , +)
→ from left (attraction), ← from right (repulsion)
Q1=-3C, Q2=+4C, Q3=+1C
Notes:
- Charge sign determines force type (repulsion/attraction)
- Distance between charges determines force strength
- Resultant force direction is determined by comparing the two forces
Analysis of Electric Forces in a Right Triangle
Geometric Configuration:
Three point charges (q₁, q₂, q₃) placed on:
- q₁ and q₂ at the short sides
- q₃ at the right angle vertex (90° angle)
Basic Coulomb's Law:
\[F=K.\frac{q_1.q_2}{r^2}\]
where kₑ = 8.99×10⁹ N·m²/C²
Steps to Calculate Resultant on q₃:
- Calculate force between q₁ and q₃ \[F_{12}=K.\frac{q_1.q_2}{a^2}\]
- Calculate force between q₂ and q₃: \[F_{23}=K.\frac{q_2.q_3}{b^2}\]
- Resolve forces into components:
- F₁₃ → horizontal component (F₁₃x) and vertical component (F₁₃y)
- F₂₃ → horizontal component (F₂₃x) and vertical component (F₂₃y)
- Total resultant:
\[Fₜₒₜₐₗ_x = ΣFₓ\]
\[Fₜₒₜₐₗ_y = ΣFᵧ\]
Determining Resultant Direction:
\[ θ = tan^{-1}\frac {(Fₜₒₜₐₗ_y )}{ (Fₜₒₜₐₗ_x)}\]
Important Notes:
- Consider charge signs (attraction/repulsion)
- Distances calculated using Pythagorean theorem if needed
- Direction depends on charge nature:
Charge Type
Force Direction
Similar
Repulsion
Different
Attraction
Force Between Two Charges
Three Charges in a Straight Line
Right Triangle
Resultant Electric Force
Coulomb's Law and Electric Force Test
\[1 \star\]
\[2 \star\]
\[3 \star\]
\[4 \star\]
\[5 \star\]
\[6 \star\]
\[7 \star\]
Test Result
You answered 0 out of 7 questions correctly
قانون كولوم |
قانون كولوم
العوامل المؤثرة على القوة الكهربائية بين شحنتين
قانون كولوم:
العوامل الرئيسية:
-
مقدار الشحنتين (q₁ و q₂):
العلاقة طردية مع حاصل ضرب الشحنتين
مثال: إذا تضاعفت إحدى الشحنتي
→ تتضاعف القوة -
المسافة بينهما (r):
العلاقة عكسية مع مربع المسافة
مثال: إذا زادت المسافة الضعف
→ تقل القوة إلى الربع -
الوسط المادي (k):
ثابت العزل الكهربائي يعتمد على الوسط:
k = 1/(4πε₀εᵣ)
حيث εᵣ هي السماحية النسبية للوسط
العلاقة الرياضية:
- \[F ∝ q₁q₂ \](طردية)
- \[F ∝\frac { 1}{r²} \](عكسية تربيعية)
- \[F ∝ \frac {1}{εᵣ }\](عكسية مع سماحية الوسط)
القوة الكهربائية بين شحنتين
قانون كولوم
القوة الكهربائية بين شحنتين نقطيتين تتناسب طرديًا مع حاصل ضرب مقدار الشحنتين وعكسيًا مع مربع المسافة بينهما :
\[F=K.\frac{q_1.q_2}{r^2}\]
حيث:
k = ثابت كولوم ≈ 8.9875×10⁹ N·m²/C²
أنواع القوى الكهربائية
1. قوة تجاذب
تحدث عندما تكون الشحنتان مختلفتين في النوع (واحدة موجبة والأخرى سالبة)
مثال: تجاذب الإلكترونات للنواة في الذرة
2. قوة تنافر
تحدث عندما تكون الشحنتان متشابهتين في النوع (كلتاهما موجبتان أو سالبتان)
مثال: تنافر شحنتين على بالونين مشحونين بنفس النوع
خصائص هامة
- قوة متبادلة (تساوي في المقدار وتعاكس في الاتجاه)
- قوة مركزية (تقع على الخط الواصل بين الشحنتين)
- تقل شدتها بزيادة المسافة بين الشحنتين
- تعتمد على الوسط العازل بين الشحنتين
تطبيقات عملية
- تصميم الدوائر الإلكترونية
- عمل المكثفات الكهربائية
- ظاهرة البرق
- الطابعات الليزرية
ملاحظات هامة:
1. القوة تنافرية إذا كانت الشحنتين متشابهتين
2. القوة تجاذبية إذا كانت الشحنتين مختلفتين
3. وحدة القوة: نيوتن (N)
4. التأثير المتبادل وفق قانون نيوتن الثالث
القوة الكهربائية بين ثلاث شحنات على خط مستقيم
قانون كولوم:
القوة بين شحنتين: \[F=K.\frac{q_1.q_2}{r^2}\]
آلية تحديد القوة المحصلة:
- حدد اتجاه القوة بين كل زوج (تنافر ←← أو تجاذب →←)
- احسب مقدار القوة بين كل زوج باستخدام القانون
- اجمع القوى بشكل متجهي حسب اتجاهها
جدول تحديد الاتجاه (للشحنة الوسطى):
| ترتيب الشحنات | اتجاه القوة | مثال |
|---|---|---|
| (+ , + , +) | ← إذا كانت أقرب لليسار، → إذا أقرب لليمين | Q1=+2C, Q2=+3C, Q3=+5C |
| (- , - , -) | → إذا كانت أقرب لليسار، ← إذا أقرب لليمين | Q1=-4C, Q2=-1C, Q3=-3C |
| (+ , + , -) | ← من اليسار (تنافر)، → من اليمين (تجاذب) | Q1=+5C, Q2=+2C, Q3=-6C |
| (- , + , +) | → من اليسار (تجاذب)، ← من اليمين (تنافر) | Q1=-3C, Q2=+4C, Q3=+1C |
ملاحظات:
- علامة الشحنة تحدد نوع القوة (تنافر/تجاذب)
- المسافة بين الشحنات تحدد شدة القوة
- اتجاه القوة المحصلة يُحدد بمقارنة شدتي القوتين
تحليل القوى الكهربائية في مثلث قائم
التركيب الهندسي:
ثلاث شحنات نقطية (q₁، q₂، q₃) موضوعة على:
- q₁ و q₂ عند الضلعين القصيرين
- q₃ عند الرأس القائم (الزاوية 90°)
قانون كولوم الأساسي:
\[F=K.\frac{q_1.q_2}{r^2}\]حيث kₑ = 8.99×10⁹ N·m²/C²
خطوات حساب المحصلة على q₃:
- احسب القوة بين q₁ و q₃ \[F_{12}=K.\frac{q_1.q_2}{a^2}\]
- احسب القوة بين q₂ و q₃: \[F_{23}=K.\frac{q_2.q_3}{b^2}\]
- حلل القوى إلى مركبات:
- F₁₃ → مركبة أفقية (F₁₃x) ومركبة رأسية (F₁₃y)
- F₂₃ → مركبة أفقية (F₂₃x) ومركبة رأسية (F₂₃y)
- المحصلة الكلية:
\[Fₜₒₜₐₗ_x = ΣFₓ\]
\[Fₜₒₜₐₗ_y = ΣFᵧ\]
تحديد اتجاه المحصلة:
\[ θ = tan^{-1}\frac {(Fₜₒₜₐₗ_y )}{ (Fₜₒₜₐₗ_x)}\]
ملاحظات هامة:
- تأخذ إشارة الشحنات في الاعتبار (تجاذب/تنافر)
- المسافات تُحسب باستخدام نظرية فيثاغورث إذا لزم الأمر
- الاتجاه يعتمد على طبيعة الشحنات:
نوع الشحنات اتجاه القوة متماثلة تنافر مختلفة تجاذب
القوة بين شحنتين
ثلاث شحنات على خط مستقيم
مثلث قائم الزاوية
القوة الكهربائية المحصلة
اختبار قانون كولوم والقوة الكهربائية
\[1 \star\] \[2 \star\] \[3 \star\] \[4 \star\] \[5 \star\] \[6 \star\] \[7 \star\]نتيجة الاختبار
لقد أجبت على 0 من أصل 7 أسئلة بشكل صحيح
Coulomb's Law |
Coulomb's Law
Factors Affecting the Electric Force Between Two Charges
Coulomb's Law:
Main Factors:
-
Magnitude of the Charges (q₁ and q₂):
Directly proportional to the product of the charges
Example: If one charge doubles
→ The force doubles -
Distance Between Them (r):
Inversely proportional to the square of the distance
Example: If the distance doubles
→ The force decreases to one-fourth -
Medium (k):
Dielectric constant depends on the medium:
k = 1/(4πε₀εᵣ)
where εᵣ is the relative permittivity of the medium
Mathematical Relationships:
- \[F ∝ q₁q₂ \](Direct)
- \[F ∝\frac { 1}{r²} \](Inverse square)
- \[F ∝ \frac {1}{εᵣ }\](Inverse with medium permittivity)
Electric Force Between Two Charges
Coulomb's Law
The electric force between two point charges is directly proportional to the product of the charges and inversely proportional to the square of the distance between them:
\[F=K.\frac{q_1.q_2}{r^2}\]
Where:
k = Coulomb's constant ≈ 8.9875×10⁹ N·m²/C²
Types of Electric Forces
1. Attractive Force
Occurs when the charges are of opposite types (one positive and one negative)
Example: Attraction between electrons and nucleus in an atom
2. Repulsive Force
Occurs when the charges are of the same type (both positive or both negative)
Example: Repulsion between two similarly charged balloons
Important Properties
- Mutual force (equal in magnitude and opposite in direction)
- Central force (acts along the line joining the charges)
- Decreases with increasing distance between charges
- Depends on the insulating medium between charges
Practical Applications
- Design of electronic circuits
- Operation of capacitors
- Lightning phenomenon
- Laser printers
Important Notes:
1. Force is repulsive if charges are similar
2. Force is attractive if charges are different
3. Unit of force: Newton (N)
4. Mutual interaction according to Newton's third law
Electric Force Between Three Charges in a Straight Line
Coulomb's Law:
Force between two charges: \[F=K.\frac{q_1.q_2}{r^2}\]
Method for Determining Resultant Force:
- Determine direction of force between each pair (repulsion ←← or attraction →←)
- Calculate magnitude of force between each pair using the law
- Add forces vectorially according to their direction
Direction Determination Table (for the middle charge):
| Charge Arrangement | Force Direction | Example |
|---|---|---|
| (+ , + , +) | ← if closer to left, → if closer to right | Q1=+2C, Q2=+3C, Q3=+5C |
| (- , - , -) | → if closer to left, ← if closer to right | Q1=-4C, Q2=-1C, Q3=-3C |
| (+ , + , -) | ← from left (repulsion), → from right (attraction) | Q1=+5C, Q2=+2C, Q3=-6C |
| (- , + , +) | → from left (attraction), ← from right (repulsion) | Q1=-3C, Q2=+4C, Q3=+1C |
Notes:
- Charge sign determines force type (repulsion/attraction)
- Distance between charges determines force strength
- Resultant force direction is determined by comparing the two forces
Analysis of Electric Forces in a Right Triangle
Geometric Configuration:
Three point charges (q₁, q₂, q₃) placed on:
- q₁ and q₂ at the short sides
- q₃ at the right angle vertex (90° angle)
Basic Coulomb's Law:
\[F=K.\frac{q_1.q_2}{r^2}\]where kₑ = 8.99×10⁹ N·m²/C²
Steps to Calculate Resultant on q₃:
- Calculate force between q₁ and q₃ \[F_{12}=K.\frac{q_1.q_2}{a^2}\]
- Calculate force between q₂ and q₃: \[F_{23}=K.\frac{q_2.q_3}{b^2}\]
- Resolve forces into components:
- F₁₃ → horizontal component (F₁₃x) and vertical component (F₁₃y)
- F₂₃ → horizontal component (F₂₃x) and vertical component (F₂₃y)
- Total resultant:
\[Fₜₒₜₐₗ_x = ΣFₓ\]
\[Fₜₒₜₐₗ_y = ΣFᵧ\]
Determining Resultant Direction:
\[ θ = tan^{-1}\frac {(Fₜₒₜₐₗ_y )}{ (Fₜₒₜₐₗ_x)}\]
Important Notes:
- Consider charge signs (attraction/repulsion)
- Distances calculated using Pythagorean theorem if needed
- Direction depends on charge nature:
Charge Type Force Direction Similar Repulsion Different Attraction
Force Between Two Charges
Three Charges in a Straight Line
Right Triangle
Resultant Electric Force
Coulomb's Law and Electric Force Test
\[1 \star\] \[2 \star\] \[3 \star\] \[4 \star\] \[5 \star\] \[6 \star\] \[7 \star\]Test Result
You answered 0 out of 7 questions correctly
 Physics
Physics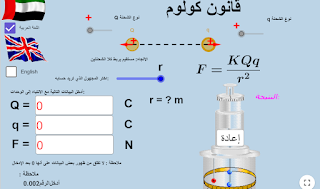
No comments:
Post a Comment