Physics
00971504825082
اسئلة مراجعة الفصل االثاني فيزياء12 متقدم حسب الهيكل( 2024-2025) |
\[1 \star\]
سلك يمر به تيار شدته \[4A\] فإن عدد الإلكترونات التي تعبر مقطع السلك خلال زمن قدره \[3S\] تعادل
اختر الإجابة الصحيحة
A
\[8.3 \times 10^{20}\] إلكترون
B
\[7.5 \times 10^{19}\] إلكترون
C
\[2.8 \times 10^{20}\] إلكترون
D
\[9.6 \times 10^{19}\] إلكترون
اضغط هنا تظهر طريقة الحل
\[2 \star\]
كمية من الشحنة تمر عبر مقطع سلك تتغير بتغير الزمن وفق المعادلة التالية \[q(t)=2t^2+3\] فإن شدة التيار المار في السلك بعد نصف ثانية تعادل
اختر الإجابة الصحيحة
A
\[i=3\;\; A\]
B
\[i=1\;\; A\]
C
\[i=2\;\; A\]
D
\[i=4\;\; A\]
اضغط هنا تظهر طريقة الحل
\[3 \star\]
سلك موصل نصف قطره \[r=0.1\;\;mm\] يمر به تيار ومقدار الشحنة التي تعبر مقطع السلك \[q=1.5 \;\;C\] خلال زمن قدره \[t=3\;\;S\] فإن كثافة التيار تعادل
اختر الإجابة الصحيحة
A
\[J=8.3 ×10^{6}\;A/m^2\]
B
\[J=18.8 ×10^{6}\;A/m^2\]
C
\[J=15.9 ×10^{6}\;A/m^2\]
D
\[J=5.72 ×10^{6}\;A/m^2\]
اضغط هنا تظهر طريقة الحل
\[4 \star\]
سلكان من النحاس لهما نفس الطول ومن نفس المادة وبنفس درجة الحرارة، تم وصلها على التوالي، نصف قطر الأول يعادل ضعف نصف قطر الثاني، فإن النسبة بين كثافة التيار للسلك الأول إلى السلك الثاني تعادل
اختر الإجابة الصحيحة
A
\[\frac {j_1}{j_2}=4\]
B
\[\frac {j_1}{j_2}=0.5\]
C
\[\frac {j_1}{j_2}=2\]
D
\[\frac {j_1}{j_2}=0.25\]
اضغط هنا تظهر طريقة الحل
\[5 \star\]
سلكان من نفس المادة وبنفس درجة الحرارة كما في الشكل أدناه فإذا كان طول السلك الأول نصف طول السلك الثاني ونصف قطر السلك الأول ضعف نصف قطر السلك الثاني فإن النسبة بين مقاومة السلك 1 إلى السلك 2 تعادل
اختر الإجابة الصحيحة
A
\[8\]
B
\[0.125\]
C
\[4\]
D
\[0.25\]
اضغط هنا تظهر طريقة الحل
\[6 \star\]
سلك مجهول النوع طوله ونصف قطر مقطعه
\[L=100\;\;m\;\;\;\;\;\;,\;\;\;\;\;\;r=1\;\;mm\]
تم حساب مقاومة السلك من خلال قانون أوم فكانت
\[R= 0.547\;\;Ω\]
من خلال البيانات السابقة وجدول المقاومات النوعية التي تم قياسها في درجة حرارة التجربة فإن السلك مصنوع من
\[𝜌=1.718 ×10^{−8} \;\; Ω.𝑚 \;\;\;\;\;\; \]
نحاس
\[𝜌=1.62 ×10^{−8}\;\; Ω.𝑚 \]
فضة
\[𝜌=2.82 ×10^{−8} \;\; Ω.𝑚 \;\;\;\;\;\; \]
ألمنيوم
\[𝜌=2.44 ×10^{−8} \;\; Ω.𝑚 \;\;\;\;\;\; \]
ذهب
اختر الإجابة الصحيحة
A
فضة
B
ذهب
C
نحاس
D
ألمنيوم
اضغط هنا تظهر طريقة الحل
\[7 \star\]
مقاومتين متساويتين عند توصيل المفتاح \[S\] في الدائرة أدناه فإن قراءة الأميتر في الدائرة
اختر الإجابة الصحيحة
A
تقل للنصف
B
تزداد للضعف
C
تزداد أربع أضعاف
D
تبقى كما هي
اضغط هنا تظهر طريقة الحل
\[8 \star\]
في الدائرة أدناه تم قياس شدة التيار فكانت تعادل \[I=4\;\;A\]
طلب من متعلم تقليل شدة التيار إلى النصف فإن الاجراء المتبع لذلك
اختر الإجابة الصحيحة
A
زيادة المقاومة إلى الضعف أو زيادة جهد المصدر إلى الضعف
B
تقليل المقاومة إلى النصف أو تقليل جهد المصدر إلى النصف
C
تقليل المقاومة إلى النصف أو زيادة جهد المصدر إلى الضعف
D
زيادة المقاومة إلى الضعف أو تقليل جهد المصدر إلى النصف
اضغط هنا تظهر طريقة الحل
\[9 \star\]
ثلاث مقاومات متصلة على التوالي
\[𝑅_1=5\;𝝮\;\;\;\;\;\;\;\;\; 𝑅_2=10\;𝝮 \;\;\;\;\;\;\;\;\; 𝑅_3=?\]
وكانت قراءة الأميتر والفولتميتر
\[I=0.6\; 𝐴 \;\;\;\;\;\;\;\;\; 𝑉=18\; 𝑉\]
فإن قيمة المقاوم الثالث تعادل
اختر الإجابة الصحيحة
A
\[R_3 =10 \;𝝮\]
B
\[R_3 =5 \;𝝮\]
C
\[R_3=20 \;𝝮\]
D
\[R_3 =15 \;𝝮\]
اضغط هنا تظهر طريقة الحل
\[10 \star\]
ثلاث مقاومات متصلة على التوالي كما في الشكل أدناه تم حساب المقاومة المكافئة فكانت \[25 Ω\] فإن قيمة المقاوم الثاني تعادل
اختر الإجابة الصحيحة
A
\[R_2= 7\;\; Ω\]
B
\[R_2= 11\;\; Ω\]
C
\[R_2= 9\;\; Ω\]
D
\[R_2= 13\;\; Ω\]
اضغط هنا تظهر طريقة الحل
\[11 \star\]
ثلاث مقاومات متصلة على التوازي كما في الشكل أدناه تم حساب المقاومة المكافئة فكانت \[6 Ω\] فإن قيمة المقاوم الثاني تعادل
اختر الإجابة الصحيحة
A
\[R_2= 10\;\; Ω\]
B
\[R_2= 20\;\; Ω\]
C
\[R_2= 30\;\; Ω\]
D
\[R_2= 40\;\; Ω\]
اضغط هنا تظهر طريقة الحل
\[12 \star\star\]
مكيف هواء يعمل من خلال تيار شدته \[I=10\;\;A\] ويحتوي على مقاومة داخلية قدرها \[R=15 \;\;𝝮\] فإن القدرة الكهربائية للمكيف تعادل
اختر الإجابة الصحيحة
A
\[P=150 \;W\]
B
\[P =2250 \;W\]
C
\[P =1500\;W\]
D
\[P = 1200\;W\]
اضغط هنا تظهر طريقة الحل
\[13 \star\star\]
مصباح كتب علية \[100\; W\;\;\;\;\;,\;\;\;\; 220\;V\] تم توصيلة ببطارية قوتها المحركة \[50\;V\] فإن قدرة المصباح تصبح
اختر الإجابة الصحيحة
A
\[P=12.7 \;W\]
B
\[P =50 \;W\]
C
\[P =25 \;W\]
D
\[P = 5.2 \;W\]
اضغط هنا تظهر طريقة الحل
\[14 \star\star\star\]
في الشكل أدناه فرق الجهد بين طرفي المقاوم الأول والثالث على الترتيب يعادل
اختر الإجابة الصحيحة
A
\[V1=7\; V \;\;\;\;\;\; ,\;\;\;\;\;\; V3=2 \;V\]
B
\[V1=5\; V \;\;\;\;\;\; ,\;\;\;\;\;\; V3=7 \;V\]
C
\[V1=7\; V \;\;\;\;\;\; ,\;\;\;\;\;\; V3=5 \;V\]
D
\[V1=2\; V \;\;\;\;\;\; ,\;\;\;\;\;\; V3=7 \;V\]
اضغط هنا تظهر طريقة الحل
\[15 \star\]
حسب قانون كيرشوف الأول فإن شدة التيار \[I_2=?\] واتجاهه يعادل
اختر الإجابة الصحيحة
A
\[i_2 =5 \;A\;\;\;\;\;\; \] للداخل
B
\[i_2 =15 \;A\;\;\;\;\;\; \] للداخل
C
\[i_2 = 3 \;A\ \;\;\;\;\;\; \] للخارج
D
\[i_2 =7 \;A \;\;\;\;\;\; \] للخارج
اضغط هنا تظهر طريقة الحل
\[16 \star\]
في الشكل ادناه شدة التيار المار في \[ R_1 , R_2 \] تعادل
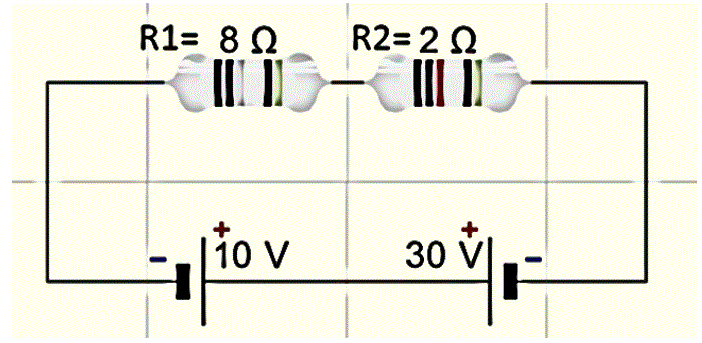
اختر الإجابة الصحيحة
A
\[I_1 = 2\;A \;\;\;\;\;\;, \;\;\;\;\;\;I_2 =2 \;A -C\]
B
\[I_1 = 1\;A \;\;\;\;\;\;, \;\;\;\;\;\;I_2 =4 \;A -A\]
C
\[I_1 = 1\;A \;\;\;\;\;\;, \;\;\;\;\;\;I_2 =4 \;A -D\]
D
\[I_1 = 1\;A \;\;\;\;\;\;, \;\;\;\;\;\;I_2 =1 \;A -B\]
اضغط هنا تظهر طريقة الحل
\[17 \star\star\star\]
جهاز الفولتميتر يستخدم لقياس فرق الجهد ويتم توصيله على التوازي في الدائرة. لزيادة مدى جهاز الفولتميتر في القياس يتم توصيل
اختر الإجابة الصحيحة
A
مقاومة صغيرة على التوازي
B
مقاومة صغيرة على التوالي
C
مقاومة عالية القيمة على التوالي
D
مقاومة عالية القيمة على التوازي
اضغط هنا تظهر طريقة الحل
\[18 \star\]
جهاز الأميتر يستخدم لقياس شدة التيار ويتم توصيله على التوالي في الدائرة. لزيادة مدى جهاز الأميتر في القياس يتم توصيل
اختر الإجابة الصحيحة
A
مقاومة صغيرة على التوالي
B
مقاومة صغيرة على التوازي
C
مقاومة عالية القيمة على التوازي
D
مقاومة عالية القيمة على التوالي
اضغط هنا تظهر طريقة الحل
\[19 \star\star\]
مكثف سعته \[c=6\;\;μF\] مشحون بشكل كامل بوساطة بطارية فرق جهدها \[V=18\;\;V\] يفرغ عبر مقاوم \[R=1\;\;kΩ\] متصل معه على التوالي. بعد زمن قدره \[t=6 \;\;ms\] فإن الشحنة المتبقية في المكثف تعادل
اختر الإجابة الصحيحة
A
\[q_t=0.14\;\; μc\]
B
\[q_t=0.39\;\; μc\]
C
\[q_t=0.83\;\; μc\]
D
\[q_t=1.24\;\; μc\]
اضغط هنا تظهر طريقة الحل
\[20 \star\star\star\]
مكثف سعته \[20𝜇𝐹\] غير مشحون تم وصله بمقاوم \[150 Ω\] على التوالي و بطارية كما في الشكل أدناه فإن النسبة المئوية لشحن المكثف بعد زمن قدره \[3 ms\] تعادل
اختر الإجابة الصحيحة
A
\[0.75\]
B
\[0.63\]
C
\[0.47\]
D
\[0.82\]
اضغط هنا تظهر طريقة الحل
\[21 \star\]
مغناطيسين تم وضعهما كما في الشكل فإن اتجاه المجال المغناطيسي عند النقطة
\[O\]
اختر الإجابة الصحيحة
A
\[\nearrow\;\;\;\;\;\;-C\] الشمال الشرقي
B
\[\longrightarrow \;\;\;\;\;\;-A\] الشرق
C
\[\nwarrow \;\;\;\;\;\;-D\] الشمال الغربي
D
\[\uparrow\;\;\;\;\;\;-B\] الشمال
اضغط هنا تظهر طريقة الحل
\[22 \star\]
حلقة تيار دائرية نصف قطرها \[r=2\;cm\] تحمل تيارًا قدره \[i=0.1\;\;A\] وخاضعة لمجال مغناطيسي شدته \[B=0.5 \;\;T\] إذا كان المجال يصنع زاوية 30 درجة مع العمود على السطح فإن مقدار العزم المغناطيسي لثنائي القطب التي تتعرض له وعزم الدوران للحلقة يعادل
اختر الإجابة الصحيحة
A
\[ 𝜇=5.23×10^{-4} \;\;A.m^2\;\;\;\;\;\;𝜏=4.6×10^{-5}N.m\]
B
\[𝜇=2.15×10^{-4} \;\;A.m^2\;\;\;\;\;\;𝜏=2.3×10^{-5}N.m\]
C
\[𝜇=3.86×10^{-4} \;\;A.m^2\;\;\;\;\;\;𝜏=1.8×10^{-5}N.m\]
D
\[𝜇=1.25×10^{-4} \;\;A.m^2\;\;\;\;\;\;𝜏=3.1×10^{-5}N.m\]
اضغط هنا تظهر طريقة الحل
\[23 \star\]
ملف يتكون من 100 حلقة وهي على شكل مربع طول ضلعه \[0.2 \;m\] ويمر بها تيار شدته \[3\;A\] وموضوع في مجال مغناطيسي شدته \[0.5\;T\] فإن الحد الأقصى لعزم الدوران يعادل
اختر الإجابة الصحيحة
A
\[𝜏_{max}= 10 \;\;N.m\]
B
\[𝜏_{max}= 6\;\;N.m\]
C
\[ 𝜏_{max}= 4\;\;N.m\]
D
\[𝜏_{max}= 8\;\;N.m\]
اضغط هنا تظهر طريقة الحل
\[24 \star\]
حلقة سلكية مربعة طول ضلعها \[20\;Cm\] ويمر بها تيار شدته \[I\] تم حساب المجال المغناطيسي الناتج من التيار المستمر في مركز الحلقة فكانت شدة المجال \[B= 0.4 mT \] نحو خارج الصفحة فإن مقدار و اتجاه التيار المار في الحلقة يعادل
اختر الإجابة الصحيحة
A
\[ i =50 \;\;A\] عكس عقارب الساعة
B
\[ i =100 \;\;A\] عكس عقارب الساعة
C
\[𝑖= 2\;\; A\] عمودي للداخل
D
\[𝑖= 4 \;\;A\] عمودي للخارج
اضغط هنا تظهر طريقة الحل
\[25 \star\]
سلك طويل يمر به التيار كما في الشكل فإن النسبة بين مجال النقطة \[a\] إلى مجال النقطة \[b\]
اختر الإجابة الصحيحة
A
\[\frac {B_a}{B_b}=9\]
B
\[\frac {B_a}{B_b}=4\]
C
\[ \frac {B_a}{B_b} =3\]
D
\[\frac {B_a}{B_b}=2\]
اضغط هنا تظهر طريقة الحل
\[26 \star\]
سلك عمودي على الورقة تم حساب المجال المغناطيسي عند نقطة تبعد عن السلك 0.2 m فكانت قيمة المجال 4.0 × 10–6 T وكان اتجاهه يوازي الورقة نحو الأعلى فإن مقدار و اتجاه التيار في السلك يساوي ؟
اختر الإجابة الصحيحة
A
\[𝑖= 4 \;\;A\] عمودي للداخل
B
\[ 𝑖= 4 \;\;A\] عمودي للخارج
C
\[𝑖= 2\;\; A\] عمودي للداخل
D
\[𝑖= 2\;\; A\] عمودي للخارج
اضغط هنا تظهر طريقة الحل
\[27 \star\]
أحد وحدات القياس التالية تعادل وحدة قياس المجال المغناطيسي تسلا \[T\]
اختر الإجابة الصحيحة
A
\[T=\frac {Kg.m}{A.s^2}\]
B
\[T=\frac {Kg.m^2}{A.s^2}\]
C
\[T=\frac {Kg.m^2}{A.s}\]
D
\[T=\frac {Kg}{A.s^2}\]
اضغط هنا تظهر طريقة الحل
أجب عن الاسئلة التالية
\[1\star\]
المقاومة هي أداة تعمل على ممانعة مرور التيار الكهربائي ولها أنواع مختلفة
تم دراسة العلاقة بين درجة الحرارة ومقاومة كل من
( الثيرموستور –ومصباح – مقاوم أومي )
فنتج الحطوط البيانية التالية
من خلال المعلومات التي تم دراستها في فرع الكهرباء حدد تحت كل خط بياني نوع المقاومة التي تحقق ذلك
اضغط هنا تظهر طريقة الحل
\[2\star\]
في الشكل أدناه دائرة مركبه
من خلال معلومات الشكل
أوجد قيمة المقاوم
\[R_E\]
\[.........................................\;\;\;\;\;\;....................................\]
\[........................................\;\;\;\;\;\;....................................\]
\[.........................................\;\;\;\;\;\;....................................\]
\[........................................\;\;\;\;\;\;....................................\]
أوجد قيمة جهد البطارية
\[V_{tot}\]
\[.........................................\;\;\;\;\;\;....................................\]
\[........................................\;\;\;\;\;\;....................................\]
اضغط هنا تظهر طريقة الحل
\[3\star\]
في الدائرة الكهربائبة ادناه تم قياس شدة التيار المار في المقاوم
\[R_1=3\;Ω\;\;\;\;\;\;\;\;I_1=0.8\; A\]
من خلال معلومات الموضحة في الشكل احسب جهد المصدر
\[.........................................\;\;\;\;\;\;....................................\]
\[.........................................\;\;\;\;\;\;....................................\]
\[.........................................\;\;\;\;\;\;....................................\]\[.........................................\;\;\;\;\;\;....................................\]
اضغط هنا تظهر طريقة الحل
\[4\star\]
في الشكل أدناه دائرة كهربائية احسب التيار المار في المقاوم
\[R=2.5\;\;𝝮\]
\[.....................................\;\;\;\;............................................\]
\[.....................................\;\;\;\;............................................\]
\[.....................................\;\;\;\;............................................\]
احسب القدرة المصروفة في المقاوم
\[R=6\;\;𝝮\]
\[.....................................\;\;\;\;............................................\]
\[.....................................\;\;\;\;............................................\]
\[.....................................\;\;\;\;............................................\]
اضغط هنا تظهر طريقة الحل
\[5\star\star\]
تتكون الدائرة الكهربائية من أربعة مقاومات
محدد قيمتها كما في الشكل أدناه
احسب شدة التيار المار في كل مقاوم
\[.........................................\;\;\;\;\;\;....................................\]\[.........................................\;\;\;\;\;\;....................................\]
\[.........................................\;\;\;\;\;\;....................................\]\[.........................................\;\;\;\;\;\;....................................\]
\[.........................................\;\;\;\;\;\;....................................\]\[.........................................\;\;\;\;\;\;....................................\]
\[.........................................\;\;\;\;\;\;....................................\]\[.........................................\;\;\;\;\;\;....................................\]
اضغط هنا تظهر طريقة الحل
\[6\star\]
في الدائرة المركبة أدناه قيم المقاومات
\[R_1=?\;\;\;\;\;\;\;,\;\;\;\;\;\;\;R_2=10\;Ω\;\;\;\;\;\;\;,\;\;\;\;\;\;\;R_3=15\;Ω\;\;\;\;\;\;\;,\;\;\;\;\;\;\;R_4=40\;Ω\]
تم وصل المقاومات ببطاريتين
\[V_1=30 \;V\;\;\;\;\;\;\;,\;\;\;\;\;\;\;V_2=10\;V\]
فكانت شدة التيار المار في المقاوم الأول
\[I_1=0.56\;\;A\]
كما في اشكل أدناه
احسب فرق الجهد بين طرفي المقاوم الثاني
\[V_2=?\;V\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
احسب قمة المقاوم الأول
\[R_1=?\;Ω\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
اضغط هنا تظهر طريقة الحل
\[7\star\]
دخل جسيم مشحون بشحنة موجبة كتلتة
وسرعته وشحنة
\[m=6×10^{-8}\;kg\;\;\;\;\;\;\;v=6×10^4\;m/s\;\;\;\;\;\;\;q=0.005C\]
وبشكل عمودي على مجال منتظم شدته \[B=0.2 T\]للخارج كما في الشكل أدناه
العجلة المركزية التي يتحرك بها الجسيم
\[.........................................\;\;\;\;\;\;....................................\]\[.........................................\;\;\;\;\;\;....................................\] \[.........................................\;\;\;\;\;\;....................................\]\[.........................................\;\;\;\;\;\;....................................\]
احسب نصف قطر المسار الدائري الذي يتخذه الجسيم
\[.........................................\;\;\;\;\;\;....................................\]\[.........................................\;\;\;\;\;\;....................................\]
وارسم على الشكل المسار الذي يتخذه مطبق قاعدة تحديد اتجاه القوة
اضغط هنا تظهر طريقة الحل
\[8\star\]
ثلاث اسلاك يمر بها نفس التيار واتجاهه موضح على الشكل
ولها نفس الطول وضعت داخل مجال مغناطيسي منتظم
كما في الشكل
أكمل بيانات الجدول التالي بالاعتماد على الشكل وبيانات الجدول
السلك 3
السلك 2
السلك 1
المطلوب
\[............\]
\[0.1 N \]
\[............\]
مقدار القوة المغناطيسية
\[............\]
\[............\]
\[\ast\ast\ast\ast\ast\ast\]
اتجاه القوة المغناطيسية
اضغط هنا تظهر طريقة الحل
\[9\star\]
سلك مستقيم طوله
يحمل تيارًا
\[L=0.5\;\;m\;\;\;\;\;,\;\;\;\;\; I=4\;\;A\]
التيار باتجاه المحور \[X^+\]
موضوع في مجال مغناطيسي منتظم شدته
\[B=1.2\;\;T\] . في المستوى \[(X,Y )\]
إذا كانت الزاوية بين اتجاه التيار واتجاه المجال المغناطيسي
\[θ=35^0\]
اضغط هنا تظهر طريقة الحل
\[10\star\]
جسيم مشحون موجود داخل مجال مغناطيسي منتظم قذف بسرعة عموديه على مجال مغناطيسي
فإذا علمت أن شحنة وكتلة وسرعة الجسيم على الترتيب
\[q=-5×10^{--6}\;C\;\;\;\;\;\;\;m=4.5×10^{-12}\;kg\;\;\;\;\;\;\;v=8×10^4\;m/s\]اتخذ الجسيم مسار دائري نصف قطره
\[r=0.2\;\;m\] وبدأ يدور الجسيم عكس عقارب الساعة
أحسب القوة المغناطيسية المؤثرة على الجسيم وحدد الاتجاه
\[.........................................\;\;\;\;\;\;....................................\]\[.........................................\;\;\;\;\;\;....................................\] \[.........................................\;\;\;\;\;\;....................................\]\[.........................................\;\;\;\;\;\;....................................\]
أحسب المجال المغناطيسي المؤثرة على الجسيم وحدد الاتجاه
\[.........................................\;\;\;\;\;\;....................................\]\[.........................................\;\;\;\;\;\;....................................\]
\[.........................................\;\;\;\;\;\;....................................\]\[.........................................\;\;\;\;\;\;....................................\]
اضغط هنا تظهر طريقة الحل
🧮 Calculator
🗑️
✏️ قلم
سلك يمر به تيار شدته \[4A\] فإن عدد الإلكترونات التي تعبر مقطع السلك خلال زمن قدره \[3S\] تعادل
اختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
كمية من الشحنة تمر عبر مقطع سلك تتغير بتغير الزمن وفق المعادلة التالية \[q(t)=2t^2+3\] فإن شدة التيار المار في السلك بعد نصف ثانية تعادل
اختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
سلك موصل نصف قطره \[r=0.1\;\;mm\] يمر به تيار ومقدار الشحنة التي تعبر مقطع السلك \[q=1.5 \;\;C\] خلال زمن قدره \[t=3\;\;S\] فإن كثافة التيار تعادل
اختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
سلكان من النحاس لهما نفس الطول ومن نفس المادة وبنفس درجة الحرارة، تم وصلها على التوالي، نصف قطر الأول يعادل ضعف نصف قطر الثاني، فإن النسبة بين كثافة التيار للسلك الأول إلى السلك الثاني تعادل
اختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
سلكان من نفس المادة وبنفس درجة الحرارة كما في الشكل أدناه فإذا كان طول السلك الأول نصف طول السلك الثاني ونصف قطر السلك الأول ضعف نصف قطر السلك الثاني فإن النسبة بين مقاومة السلك 1 إلى السلك 2 تعادل
اختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
سلك مجهول النوع طوله ونصف قطر مقطعه
\[L=100\;\;m\;\;\;\;\;\;,\;\;\;\;\;\;r=1\;\;mm\]
تم حساب مقاومة السلك من خلال قانون أوم فكانت
\[R= 0.547\;\;Ω\]
من خلال البيانات السابقة وجدول المقاومات النوعية التي تم قياسها في درجة حرارة التجربة فإن السلك مصنوع من
\[𝜌=1.718 ×10^{−8} \;\; Ω.𝑚 \;\;\;\;\;\; \] |
\[𝜌=1.62 ×10^{−8}\;\; Ω.𝑚 \] |
\[𝜌=2.82 ×10^{−8} \;\; Ω.𝑚 \;\;\;\;\;\; \] |
\[𝜌=2.44 ×10^{−8} \;\; Ω.𝑚 \;\;\;\;\;\; \] |
اختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
مقاومتين متساويتين عند توصيل المفتاح \[S\] في الدائرة أدناه فإن قراءة الأميتر في الدائرة
اختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
في الدائرة أدناه تم قياس شدة التيار فكانت تعادل \[I=4\;\;A\]
طلب من متعلم تقليل شدة التيار إلى النصف فإن الاجراء المتبع لذلك
اختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
ثلاث مقاومات متصلة على التوالي
\[𝑅_1=5\;𝝮\;\;\;\;\;\;\;\;\; 𝑅_2=10\;𝝮 \;\;\;\;\;\;\;\;\; 𝑅_3=?\]
وكانت قراءة الأميتر والفولتميتر
\[I=0.6\; 𝐴 \;\;\;\;\;\;\;\;\; 𝑉=18\; 𝑉\]
فإن قيمة المقاوم الثالث تعادل
اختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
ثلاث مقاومات متصلة على التوالي كما في الشكل أدناه تم حساب المقاومة المكافئة فكانت \[25 Ω\] فإن قيمة المقاوم الثاني تعادل
اختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
ثلاث مقاومات متصلة على التوازي كما في الشكل أدناه تم حساب المقاومة المكافئة فكانت \[6 Ω\] فإن قيمة المقاوم الثاني تعادل
اختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
مكيف هواء يعمل من خلال تيار شدته \[I=10\;\;A\] ويحتوي على مقاومة داخلية قدرها \[R=15 \;\;𝝮\] فإن القدرة الكهربائية للمكيف تعادل
اختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
مصباح كتب علية \[100\; W\;\;\;\;\;,\;\;\;\; 220\;V\] تم توصيلة ببطارية قوتها المحركة \[50\;V\] فإن قدرة المصباح تصبح
اختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
في الشكل أدناه فرق الجهد بين طرفي المقاوم الأول والثالث على الترتيب يعادل
اختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
حسب قانون كيرشوف الأول فإن شدة التيار \[I_2=?\] واتجاهه يعادل
اختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
في الشكل ادناه شدة التيار المار في \[ R_1 , R_2 \] تعادل
اختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
جهاز الفولتميتر يستخدم لقياس فرق الجهد ويتم توصيله على التوازي في الدائرة. لزيادة مدى جهاز الفولتميتر في القياس يتم توصيل
اختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
جهاز الأميتر يستخدم لقياس شدة التيار ويتم توصيله على التوالي في الدائرة. لزيادة مدى جهاز الأميتر في القياس يتم توصيل
اختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
مكثف سعته \[c=6\;\;μF\] مشحون بشكل كامل بوساطة بطارية فرق جهدها \[V=18\;\;V\] يفرغ عبر مقاوم \[R=1\;\;kΩ\] متصل معه على التوالي. بعد زمن قدره \[t=6 \;\;ms\] فإن الشحنة المتبقية في المكثف تعادل
اختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
مكثف سعته \[20𝜇𝐹\] غير مشحون تم وصله بمقاوم \[150 Ω\] على التوالي و بطارية كما في الشكل أدناه فإن النسبة المئوية لشحن المكثف بعد زمن قدره \[3 ms\] تعادل
اختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
مغناطيسين تم وضعهما كما في الشكل فإن اتجاه المجال المغناطيسي عند النقطة \[O\]
اختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
حلقة تيار دائرية نصف قطرها \[r=2\;cm\] تحمل تيارًا قدره \[i=0.1\;\;A\] وخاضعة لمجال مغناطيسي شدته \[B=0.5 \;\;T\] إذا كان المجال يصنع زاوية 30 درجة مع العمود على السطح فإن مقدار العزم المغناطيسي لثنائي القطب التي تتعرض له وعزم الدوران للحلقة يعادل
اختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
ملف يتكون من 100 حلقة وهي على شكل مربع طول ضلعه \[0.2 \;m\] ويمر بها تيار شدته \[3\;A\] وموضوع في مجال مغناطيسي شدته \[0.5\;T\] فإن الحد الأقصى لعزم الدوران يعادل
اختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
حلقة سلكية مربعة طول ضلعها \[20\;Cm\] ويمر بها تيار شدته \[I\] تم حساب المجال المغناطيسي الناتج من التيار المستمر في مركز الحلقة فكانت شدة المجال \[B= 0.4 mT \] نحو خارج الصفحة فإن مقدار و اتجاه التيار المار في الحلقة يعادل
اختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
سلك طويل يمر به التيار كما في الشكل فإن النسبة بين مجال النقطة \[a\] إلى مجال النقطة \[b\]
اختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
سلك عمودي على الورقة تم حساب المجال المغناطيسي عند نقطة تبعد عن السلك 0.2 m فكانت قيمة المجال 4.0 × 10–6 T وكان اتجاهه يوازي الورقة نحو الأعلى فإن مقدار و اتجاه التيار في السلك يساوي ؟
اختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
أحد وحدات القياس التالية تعادل وحدة قياس المجال المغناطيسي تسلا \[T\]
اختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
أجب عن الاسئلة التالية
المقاومة هي أداة تعمل على ممانعة مرور التيار الكهربائي ولها أنواع مختلفة
تم دراسة العلاقة بين درجة الحرارة ومقاومة كل من
( الثيرموستور –ومصباح – مقاوم أومي )
فنتج الحطوط البيانية التالية
من خلال المعلومات التي تم دراستها في فرع الكهرباء حدد تحت كل خط بياني نوع المقاومة التي تحقق ذلك
اضغط هنا تظهر طريقة الحل
في الشكل أدناه دائرة مركبه
من خلال معلومات الشكل
أوجد قيمة المقاوم
\[R_E\]
\[.........................................\;\;\;\;\;\;....................................\]
\[........................................\;\;\;\;\;\;....................................\]
\[.........................................\;\;\;\;\;\;....................................\]
\[........................................\;\;\;\;\;\;....................................\]
أوجد قيمة جهد البطارية
\[V_{tot}\]
\[.........................................\;\;\;\;\;\;....................................\]
\[........................................\;\;\;\;\;\;....................................\]
اضغط هنا تظهر طريقة الحل
في الدائرة الكهربائبة ادناه تم قياس شدة التيار المار في المقاوم \[R_1=3\;Ω\;\;\;\;\;\;\;\;I_1=0.8\; A\] من خلال معلومات الموضحة في الشكل احسب جهد المصدر
اضغط هنا تظهر طريقة الحل
في الشكل أدناه دائرة كهربائية احسب التيار المار في المقاوم \[R=2.5\;\;𝝮\]
اضغط هنا تظهر طريقة الحل
تتكون الدائرة الكهربائية من أربعة مقاومات
محدد قيمتها كما في الشكل أدناه
في الدائرة المركبة أدناه قيم المقاومات
\[R_1=?\;\;\;\;\;\;\;,\;\;\;\;\;\;\;R_2=10\;Ω\;\;\;\;\;\;\;,\;\;\;\;\;\;\;R_3=15\;Ω\;\;\;\;\;\;\;,\;\;\;\;\;\;\;R_4=40\;Ω\]
تم وصل المقاومات ببطاريتين
\[V_1=30 \;V\;\;\;\;\;\;\;,\;\;\;\;\;\;\;V_2=10\;V\]
فكانت شدة التيار المار في المقاوم الأول
\[I_1=0.56\;\;A\]
كما في اشكل أدناه
دخل جسيم مشحون بشحنة موجبة كتلتة
وسرعته وشحنة
\[m=6×10^{-8}\;kg\;\;\;\;\;\;\;v=6×10^4\;m/s\;\;\;\;\;\;\;q=0.005C\]
وبشكل عمودي على مجال منتظم شدته \[B=0.2 T\]للخارج كما في الشكل أدناه
ثلاث اسلاك يمر بها نفس التيار واتجاهه موضح على الشكل
السلك 3 السلك 2 السلك 1 المطلوب \[............\] \[0.1 N \] \[............\] مقدار القوة المغناطيسية \[............\] \[............\] \[\ast\ast\ast\ast\ast\ast\] اتجاه القوة المغناطيسية سلك مستقيم طوله
يحمل تيارًا
\[L=0.5\;\;m\;\;\;\;\;,\;\;\;\;\; I=4\;\;A\]
التيار باتجاه المحور \[X^+\]
موضوع في مجال مغناطيسي منتظم شدته
\[B=1.2\;\;T\] . في المستوى \[(X,Y )\]
إذا كانت الزاوية بين اتجاه التيار واتجاه المجال المغناطيسي
\[θ=35^0\]
جسيم مشحون موجود داخل مجال مغناطيسي منتظم قذف بسرعة عموديه على مجال مغناطيسي
احسب شدة التيار المار في كل مقاوم
\[.........................................\;\;\;\;\;\;....................................\]\[.........................................\;\;\;\;\;\;....................................\]
\[.........................................\;\;\;\;\;\;....................................\]\[.........................................\;\;\;\;\;\;....................................\]
\[.........................................\;\;\;\;\;\;....................................\]\[.........................................\;\;\;\;\;\;....................................\]
\[.........................................\;\;\;\;\;\;....................................\]\[.........................................\;\;\;\;\;\;....................................\]
اضغط هنا تظهر طريقة الحل
احسب فرق الجهد بين طرفي المقاوم الثاني
\[V_2=?\;V\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
احسب قمة المقاوم الأول
\[R_1=?\;Ω\]
\[........................................................................................\]
\[........................................................................................\]
\[........................................................................................\]
اضغط هنا تظهر طريقة الحل
العجلة المركزية التي يتحرك بها الجسيم
\[.........................................\;\;\;\;\;\;....................................\]\[.........................................\;\;\;\;\;\;....................................\] \[.........................................\;\;\;\;\;\;....................................\]\[.........................................\;\;\;\;\;\;....................................\]
احسب نصف قطر المسار الدائري الذي يتخذه الجسيم
\[.........................................\;\;\;\;\;\;....................................\]\[.........................................\;\;\;\;\;\;....................................\]
وارسم على الشكل المسار الذي يتخذه مطبق قاعدة تحديد اتجاه القوة
اضغط هنا تظهر طريقة الحل
ولها نفس الطول وضعت داخل مجال مغناطيسي منتظم
كما في الشكل
أكمل بيانات الجدول التالي بالاعتماد على الشكل وبيانات الجدول
اضغط هنا تظهر طريقة الحل
اضغط هنا تظهر طريقة الحل
فإذا علمت أن شحنة وكتلة وسرعة الجسيم على الترتيب
\[q=-5×10^{--6}\;C\;\;\;\;\;\;\;m=4.5×10^{-12}\;kg\;\;\;\;\;\;\;v=8×10^4\;m/s\]اتخذ الجسيم مسار دائري نصف قطره
\[r=0.2\;\;m\] وبدأ يدور الجسيم عكس عقارب الساعة
أحسب القوة المغناطيسية المؤثرة على الجسيم وحدد الاتجاه
\[.........................................\;\;\;\;\;\;....................................\]\[.........................................\;\;\;\;\;\;....................................\] \[.........................................\;\;\;\;\;\;....................................\]\[.........................................\;\;\;\;\;\;....................................\]
أحسب المجال المغناطيسي المؤثرة على الجسيم وحدد الاتجاه
\[.........................................\;\;\;\;\;\;....................................\]\[.........................................\;\;\;\;\;\;....................................\]
\[.........................................\;\;\;\;\;\;....................................\]\[.........................................\;\;\;\;\;\;....................................\]
اضغط هنا تظهر طريقة الحل
No comments:
Post a Comment