📄 اطبع pdf
00971504825082

<<< أسئلة مراجعة الفصل الثالث فيزياء 11 متقدم حسب الهيكل ( 2023-2024) >>>

رَبِّ أَوْزِعْنِي أَنْ أَشْكُرَ نِعْمَتَكَ الَّتِي أَنْعَمْتَ عَلَيَّ وَعَلَى وَالِدَيَّ وَأَنْ أَعْمَلَ صَالِحًا تَرْضَاهُ وَأَصْلِحْ لِي فِي ذُرِّيَّتِي إِنِّي تُبْتُ إِلَيْكَ وَإِنِّي مِنَ الْمُسْلِمِينَ .

رَبَّنَا هَبْ لَنَا مِنْ أَزْوَاجِنَا وَذُرِّيَّاتِنَا قُرَّةَ أَعْيُنٍ وَاجْعَلْنَا لِلْمُتَّقِينَ إِمَامًا

رَبِّ هَبْ لِي حُكْمًا وَأَلْحِقْنِي بِالصَّالِحِينَ واجْعَل لِّي لِسَانَ صِدْقٍ فِي الآخِرِينَ وَاجْعَلْنِي مِن وَرَثَةِ جَنَّةِ النَّعِيمِ

\[1 \star\]

يتم تحديد مركز الكتلة لجسم من خلال تحديد

اختر الإجابة الصحيحة

---

A

نقطة في الجسم تتركز فيها كتلة الجسم كلها

B

المركز الهندسي للجسم الذي له كثافة ثابتة

C

نقطة تكون هي مركز اتزان الجسم

D

جميع ما سبق

اضغط هنا تظهر طريقة الحل

\[2 \star\]

جسمين غير متساويان في الكتلة. فإن مركز الكتلة المشترك لهما مهما كان موقع نظام الإحداثيات يكون دوما

اختر الإجابة الصحيحة

---

A

أقرب للجسم الأصغر

B

أقرب للجسم الأكبر

C

في منتصف المسافة بين الجسمين

D

على امتداد الخط الواصل بين الجسمين

اضغط هنا تظهر طريقة الحل

\[3 \star\]

(4 kg) حجر كتلته m=4 Kg تم قذفة بوساطة منجنيق فسقط الحجر على بعد 180 متر من المنجنيق في المرة الثانية تفتت الحجر إلى قطعتين ووصلت إلى الأرض بنفس الوقت وبفرض اهمال مقاومة الهواء فسقطت القطعة الأولى التي كتلتها 1 kg على بعد 240 متر فإن القطعة الثانية تكون سقطت على بعد

اختر الإجابة الصحيحة

---

A

X=160 m

B

X=130 m

C

X=120 m

D

X=150 m

اضغط هنا تظهر طريقة الحل

\[4 \star\]

الإحداثيات الديكارتية لجسم هي (-3 , 10) فإن الإحداثيات القطبية له

اختر الإجابة الصحيحة

---

A

(14.34 , 101.2⁰)

B

(12.44 , 117.8⁰)

C

(10.44 , 106.7⁰)

D

(14.34 , 101.2⁰)

اضغط هنا تظهر طريقة الحل

\[5 \star\]

الإحداثيات القطبية لجسم هي (13 , 22.6⁰) فإن الإحداثيات الديكارتية له

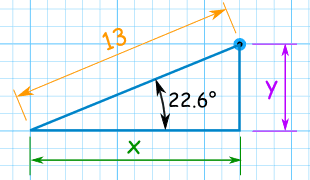
اختر الإجابة الصحيحة

---

A

(9,7)

B

(8,5)

C

(12,5)

D

(10,3)

اضغط هنا تظهر طريقة الحل

\[6 \star\]

جسم يتحرك حركة دائرية مع عقارب الساعة نصف قطرها r=30 cm وقطع مسافة قدرها s=2 m فإن الإزاحة الزاوية للحركة تعادل

اختر الإجابة الصحيحة

---

A

𝜃=6.67 rad

B

𝜃=-60 rad

C

𝜃=-6.67 rad

D

𝜃=60 rad

اضغط هنا تظهر طريقة الحل

\[7 \star \star\]

جسم يتحرك حركة دائرية فقطع إزاحة زاوية قدرها \[65^0\] مع عقارب الساعة فإن الإزاحة الزاوية تعادل بوحدة الراديان

اختر الإجابة الصحيحة

---

A

𝜃= -1.53 𝑟𝑎𝑑

B

𝜃= 1.53 𝑟𝑎𝑑

C

𝜃= −1.13 𝑟𝑎𝑑

D

𝜃= 1.13 𝑟𝑎𝑑

اضغط هنا تظهر طريقة الحل

\[8 \star\]

أحد الإجابات التالية تعادل السرعة الزاوية لعقرب الدقائق

اختر الإجابة الصحيحة

---

A

W = -0.104 𝑟𝑎𝑑/𝑠

B

W = 0.104 𝑟𝑎𝑑/𝑠

C

W = 1.74 × 10^-3 rad/s

D

W = −1.74 × 10^-3 rad/s

اضغط هنا تظهر طريقة الحل

\[9 \star\]

يتحرك جسم حركة دائرية منتظمة بحيث يعمل ثلاث دورات ونصف عكس عقارب الساعة كل 2 ثانية فإن سرعته الزاوية بوحدة rad/s

اختر الإجابة الصحيحة

---

A

W = 4𝜋 rad/s

B

W = 7𝜋 rad/s

C

W = 6𝜋 rad/s

D

W = 3.5𝜋 rad/s

اضغط هنا تظهر طريقة الحل

\[10 \star\]

يتحرك قمر صناعي في مسار دائري منتظم حول الأرض نصف قطر المسار الدائري (8500)Km حيث كان زمنه الدوري 2(day) سرعته الخطية تساوي

اختر الإجابة الصحيحة

---

A

v = 210 𝑚/𝑠

B

v = 412 𝑚/𝑠

C

v = 309 𝑚/𝑠

D

v = 518 𝑚/𝑠

اضغط هنا تظهر طريقة الحل

\[11 \star \star\]

جسيم يتحرك حركة دائرية مع عقارب الساعة نصف قطرها r=0.4m في لحظة ما تم قياس سرعة الجسم الخطية فكانت v=0.6m/s وكان التسارع الكلي يعادل a=1.2m/s² فإن التسارع المماسي عند تلك اللحظة يعادل

اختر الإجابة الصحيحة

---

A

at=0.3m/s²

B

at=0.8m/s²

C

at=0.5m/s²

D

at=0.6m/s²

اضغط هنا تظهر طريقة الحل

\[12 \star\]

جسيم يتحرك حركة دائرية عكس عقارب الساعة نصف قطرها r وعند لحظة معينه كانت قيمة التسارع للجسيم السلك a=15m/s² ويصنع زاوية قدرها 20° مع متجهة السرعة الخطية فإن مقدار التسارع الخطي والتسارع المركزي يعادل

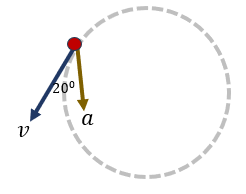
اختر الإجابة الصحيحة

---

A

at=5.3 m/s² ..........ac=14 m/s²

B

at=2.5 m/s² ..........ac=14.8 m/s²

C

at=7.5 m/s² ..........ac=13 m/s²

D

at=6.12 m/s² ..........ac=13.7 m/s²

اضغط هنا تظهر طريقة الحل

\[13 \star\]

تتحرك السيارة بسرعة ثابتة حول مسار دائري أفقي. القوة المركزية المؤثرة على السيارة تساوي دائمًا

اختر الإجابة الصحيحة

---

A

القوة الأمامية من المحرك

B

وزن السيارة

C

القوة المتعامدة

D

الاحتكاك الجانبي بين الإطارات والمسار

اضغط هنا تظهر طريقة الحل

\[14 \star\star\]

تم ربط دلو بحبل طوله 0.7 m وتم تدويره بشكل أفقي وبسرعه مماسيه قدرها \[v=2 \frac{m}{s} \] فان عجلته المركزية تعادل

اختر الإجابة الصحيحة

---

A

ac =5.7 m/s²

B

ac =3.6 m/s²

C

ac =1.4 m/s²

D

ac =5.7 m/s²

اضغط هنا تظهر طريقة الحل

\[15 \star\]

تم ربط دلو بحبل طوله 0.4 m وتم تدويره بشكل أفقي وبسرعه مماسيه قدرها \[v=2 \frac{m}{s} \] فإن الزمن الدوري للحركة يعادل

اختر الإجابة الصحيحة

---

A

T=1.26 S

B

T=3.56 S

C

T=5 S

D

T=4.12 S

اضغط هنا تظهر طريقة الحل

\[16 \star\]

جسم يتحرك حركة دائرية فقطع إزاحة زاوية قدرها \[125^0\] مع عقارب الساعة فإن الإزاحة الزاوية تعادل بوحدة الراديان

اختر الإجابة الصحيحة

---

A

𝜃= −3.53 𝑟𝑎𝑑

B

𝜃= −1.53 𝑟𝑎𝑑

C

𝜃= −2.18 𝑟𝑎𝑑

D

𝜃= −4.53 𝑟𝑎𝑑

اضغط هنا تظهر طريقة الحل

\[17 \star\star\]

يتحرك جسم حركه دائريه منتظمة بحيث يعمل عدد من الدورات قدره \[ 3.25\] دوره خلال زمن قدره \[t=6\;s\] فان سرعته الزاوية بوحدة \[\frac{rad}{s}\]

اختر الإجابة الصحيحة

---

A

W=4.5 Rad/s

B

W=3.4 Rad/s

C

W=2.5 Rad/s

D

W=5.2 Rad/s

اضغط هنا تظهر طريقة الحل

\[18 \star\]

في الحركة الدائرية المنتظمة أحد الأشكال التالية تعبر عن اتجاه السرعة الخطية والتسارع المركزي لجسم يتحرك حركة دائرية منتظمة عكس عقارب الساعة

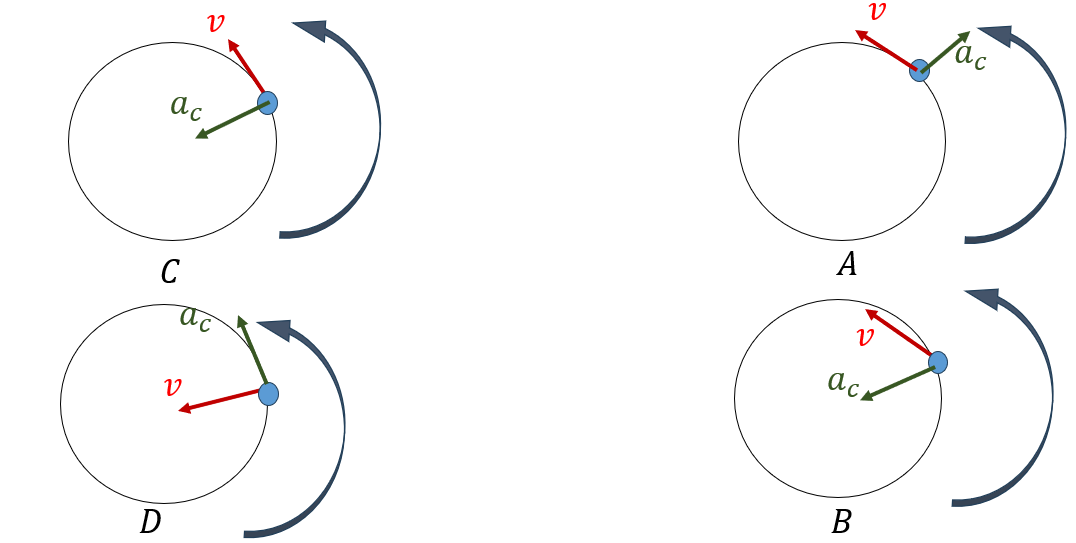
اختر الإجابة الصحيحة

---

A

A

B

B

C

C

D

D

اضغط هنا تظهر طريقة الحل

\[19 \star\]

أحد المخططات التالية يمثل العلاقة بين اتجاهات كل من السرعة الخطية و متجهة الموقغ و عجلة الجذب المركزية والقوة المركزية لجسم يتحرك حركة دائرية منتظمة

اختر الإجابة الصحيحة

---

A

A

B

B

C

C

D

D

اضغط هنا تظهر طريقة الحل

\[20 \star\star\]

أربع كرات تم ربطها بخيط وطلب من طلاب تحريك الكرة المرتبطة بخيط بشكل دائري و أفقي

وتم رصد معادلات الإزاحة الزاوية للحركة الدائرية فكانت كما في الشكل أدناه

أحد المعادلات السابقة تبين أن الجسم يتحرك حركة دائرية منتظمة

اختر الإجابة الصحيحة

---

A

\[ A \]

B

\[B\]

C

\[ C \]

D

\[ D \]

اضغط هنا تظهر طريقة الحل

\[21 \star\]

جسم يتحرك حركة دائرية تم رسم متجهة السرعة الخطية للجسم في عدة مواقع

أحد الاجابات التالية تعبر بشكل صحيح عن الحركة

اختر الإجابة الصحيحة

---

A

التسارع الخطي ناتج عن تغير مقدار السرعة الزاوية
التسارع المركزي ناتج عن تغير مقدار السرعة الخطية

B

التسارع الخطي ناتج عن تغير مقدار السرعة الخطية
التسارع المركزي ناتج عن تغير اتجاه السرعة الخطية

C

التسارع الخطي ناتج عن تغير مقدار السرعة الخطية
التسارع المركزي ناتج عن تغير مقدار السرعة الزاوية

D

التسارع الخطي ناتج عن تغير اتجاه السرعة الخطية
التسارع المركزي ناتج عن تغير مقدار السرعة الخطية

اضغط هنا تظهر طريقة الحل

\[22 \star\]

يُظهر الشكل راكبًا عالقًا على الحائط في برميل المرح في كرنفال

أي مخطط يوضح بشكل صحيح القوى المؤثرة على الراكب

اختر الإجابة الصحيحة

---

A

\[ A \]

B

\[ B \]

C

\[ C \]

D

\[ D \]

اضغط هنا تظهر طريقة الحل

أجب عن الأسئلة التالية

\[1\star \]

هناك ثلاث كرات تم ربطها بحبل وجعلت تتحرك حركة دائرية أفقية عكس عقارب الساعة كما في الشكل أدناه
حدد على كل شكل باستخدام رسم المتجهات و حسب نوع الحركة اتجاه كل من 1- السرعة الخطية
2- التسارع المماسي
3- التسارع المركزي
4-السرعة الزاوية
5-التسارع الزاوي
6-التسارع الكلي \[\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\] في الحركة الدائرية المنتظمة تم رصد الكرة في موضعين مختلفين قارن بين السرعة الخطية والسرعة الزاوية في كلا الموضعين مع بيان السبب في كل إجابة \[.........................................\;\;\;\;\;\;....................................\] \[........................................\;\;\;\;\;\;....................................\] \[.........................................\;\;\;\;\;\;....................................\] 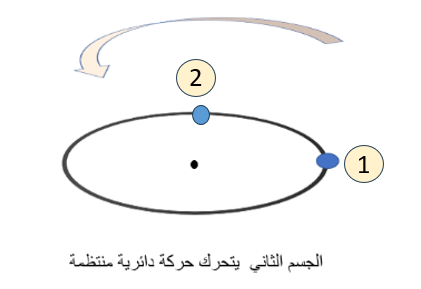إذا علمت أن السرعة الزاوية للحركة الدائرية المنتظمة تعادل \[20\;rev/min\] ونصف قطر المسار الدائري يعادل \[r=0.4\;m\] احسب السرعة الخطية للكرة \[.........................................\;\;\;\;\;\;....................................\] \[........................................\;\;\;\;\;\;....................................\] \[.........................................\;\;\;\;\;\;....................................\]

اضغط هنا تظهر طريقة الحل

\[2\star\]

في لعبة العربة الأفعوان عندما تتحرك العربة على السكة قارن بين القوة المتعامدة المؤثرة على العربة عند أعلى نقطة وعند أدنى نقطة من خلال تطبيق محصلة القوى المؤثرة على العربة \[.........................................\;\;\;\;\;\;....................................\] \[........................................\;\;\;\;\;\;....................................\] \[.........................................\;\;\;\;\;\;....................................\] \[........................................\;\;\;\;\;\;....................................\] لو فرضنا عدم وجود احتكاك بن العربة والسكة يشعر اللاعب بانعدام الوزن الظاهري عند القمة بفرض أن نصف قطر المسار الدائري \[r=8\;m\] احسب السرعة عند القمة \[g=9.81\;m/s^2\] \[.........................................\;\;\;\;\;\;....................................\] \[........................................\;\;\;\;\;\;....................................\] \[.........................................\;\;\;\;\;\;....................................\] \[........................................\;\;\;\;\;\;....................................\] باستخدام مبدأ حفظ الطاقة احسب سرعة العربة عند أدنى نقطة بفرض عدم وجود احتكاك وانعدام الوزن الظاهري عند القمة \[.........................................\;\;\;\;\;\;....................................\] \[........................................\;\;\;\;\;\;....................................\] \[.........................................\;\;\;\;\;\;....................................\] \[........................................\;\;\;\;\;\;....................................\]

اضغط هنا تظهر طريقة الحل

\[3\star\]

جسم يتحرك حركة دائرية من السكون معادلة الإزاحة الزاوية تعطى بالعلاقة \[𝜃(𝑡)=2𝑡^3−3𝑡^2+4𝑡\] فإذا علمت أن نصف قطر المسار الدائري للحركة \[r=0.3\;m\] احسب عدد الدورات خلال زمن قدره 3 ثواني \[.....................................\;\;\;\;............................................\] \[.....................................\;\;\;\;............................................\] \[.....................................\;\;\;\;............................................\] أحسب التسارع الزاوي والخطي للحركة في الثانية الثالثة \[.....................................\;\;\;\;............................................\] \[.....................................\;\;\;\;............................................\] \[.....................................\;\;\;\;............................................\] \[.....................................\;\;\;\;............................................\] \[.....................................\;\;\;\;............................................\] احسب التسارع الكلي في الثانية الثالثة \[.....................................\;\;\;\;............................................\] \[.....................................\;\;\;\;............................................\]

اضغط هنا تظهر طريقة الحل

\[4\star\star\]

تتحرك سيارة حول منعطف نصف قطره \[R=400\;m\] على طريق منحنية بزاوية مع الأفقي. إذا كانت السيارة لا تميل إلى الانزلاق عند التحرك(الاحتكاك شبه معدوم )
وتتحرك بسرعة \[v=35\;m/s\]
احسب زاوية ميل الطريق \[........................................................................................\] \[........................................................................................\] \[........................................................................................\] \[........................................................................................\] \[........................................................................................\] على فرض أن زاوية ميل المنعطف كانت \[𝜃=25^0\] ونصف قطر المنعطف هو \[R=200\; m\] وكان معامل الاحتكاك السكوني بين الطريق وإطارات السيارة يعادل \[ µ_s=0.5 \] احسب أقصى سرعة للسائق ممكن التحرك بها \[........................................................................................\] \[........................................................................................\] \[........................................................................................\] \[........................................................................................\] \[........................................................................................\] \[........................................................................................\] \[........................................................................................\]

اضغط هنا تظهر طريقة الحل

5

سيارة نصف قطر إطاراتها \[r=0.25 \;m\]تتحرك دون انزلاق بسرعة ثابتة مقدارها \[v=23\;m/s\]لمدة زمنية قدرها \[t=3\;min\] شاهد السائق مطب فطبق نظام الفرملة فتباطأت بشكل منتظم حتى توقفت بعد زمن قدره \[t=25\;s\] احسب عدد الدورات التي دارها الإطار خلال كامل الفترة تعادل \[........................................................................................\] \[........................................................................................\] \[........................................................................................\] \[........................................................................................\] \[........................................................................................\]

اضغط هنا تظهر طريقة الحل

اكتب تعليقا واذا كان هناك خطأ اكتبه وحدد مكانه Write a comment, and if there is mistake, write and specify its location

No comments:

Post a Comment

Newer Post Older Post Home