Physics
📄 اطبع pdf
00971504825082
الحركة الدورانية
الإزاحة الزاوية
تذكر : الإزاحة الخطية = الموقع النهائي – الموقع الابتدائي
\[∆X=X_2−X_1\]
الإزاحة الزاوية = الزاوية النهائية – الزاوية الابتدائية
\[∆𝜃=𝜃_2−𝜃_1\]
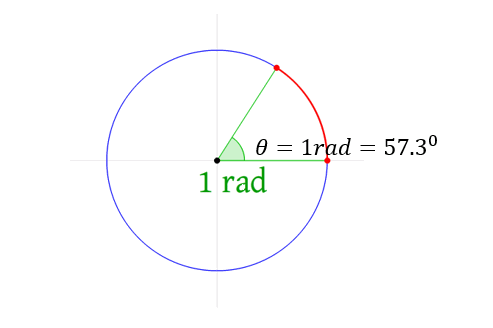
إذا تحرك جسم من نقطة الى اخرى وقطع قوس طوله \[S\] على محيط دائره نصف قطرها \[r\] فإن الزاويه التي تقابل القوس تسمى بالازاحه الزاويه ويرمز لها بالرمز \[𝜃\]
\[𝜃 =\frac{s}{r}\]
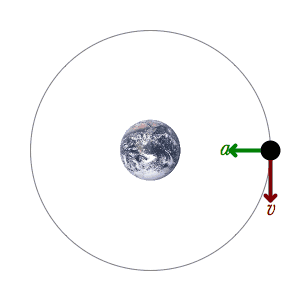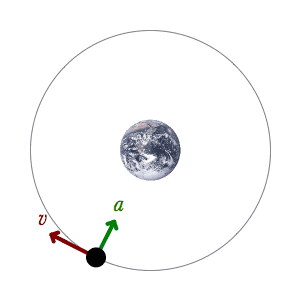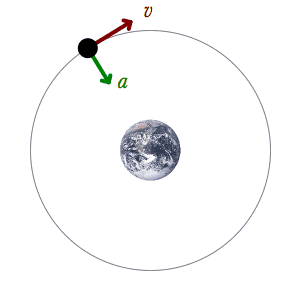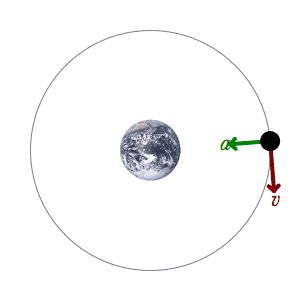
الإزاحة الزاوية كمية متجهه إذا كان الدوران عكس عقارب الساعة تأخذ إشارة موجبة وإذا كان الدوران مع عقارب الساعة تأخذ إشارة سالبة
يمثل الراديان الوحدة لقياس الإحداثيات الزاوية
(rev) قد تجد الإزاحة الزاوية بوحدة الدرجات او بوحدة الدورات
يتم تحويل الزاوية إلى الراديان حسب معاملات التحويل التالية
معامل التحويل من الدورات إلى الراديان
معامل التحويل من الدرجات إلى الراديان
\[2𝜋 (rad)= 1 rev\]
\[𝜋 (rad )= 180^0\]
مثال :جسم يتحرك حركة دائرية قطع إزاحة زاوية قدرها 2.25 دورة فكم يعادل بالراديان
مثال : جسم قطع إزاحة زاوية 120 درجة فكم يعادل بوحدة الراديان
\[ 𝜃 = 2.25 × 2𝜋 =14.13 rad \]
\[ 𝜃 = 120 ^0 × \frac{𝜋}{180}=2.1 rad \]
السرعة الزاوية
تذكر : السرعة المتجهة الخطية لجسم ما هي تغير الإحداثيات الخطية للجسم بالنسبة للزمن
السرعة الزاوية لجسم ما : هي تغير الإحداثي الزاوي للجسم مع الزمن \[W_{avg}=\frac{∆𝜃 (rad)}{∆t (s)}= \frac{𝜃_2 - 𝜃_1}{t_2 -t_1}\]
التجربة 1 قياس السرعة الزاوية
السرعة الزاوية لجسم ما : هي تغير الإحداثي الزاوي للجسم مع الزمن
( a𝛾=0.0 )اجعل الحركة الدائرية منتظمة
( 𝜃-t )اضغط على الخط البياني
الفترة الزمنية
الإزاحة الزاوية النهائية
الإزاحة الزاوية الإبتدئية
\[t_2 -t_1= ....s\]
\[𝜃_2= .....rad\]
\[𝜃_1= ....rad\]
السرعة الزاوية
اتجاه السرعة الزاوية
\[W= \frac{𝜃_2 - 𝜃_1}{t_2 -t_1}= ......rad/s\] السرعة الزاوية معدل تغير الزاوية خلال الزمن
إذا كان الدوران عكس عقارب الساعة
إذا كان الدوران بإتجاه عقارب الساعة
\[1 \star\]
يتحرك جسم حركه دائريه منتظمة بحيث يعمل دوره واحده كل ثانيه فان سرعته الزاوية بوحدة \[rad/s\]
أختر الإجابة الصحيحة
A
w= 4𝜋 rad/s
B
w= 𝜋 rad/s
C
w= 2𝜋 rad/s
D
w= 3𝜋 rad/s
\[2 \star\]
مروحه تدور بسرعه بزاويه قدرها
(60 𝜋 rad/s)
فان الزاوية التي تقطعها أحد شفراتها خلال زمن قدره \[t=3 \;s \] تعادل
أختر الإجابة الصحيحة
A
∆𝜃=120 𝜋 rad
B
∆𝜃=60 𝜋 rad
C
∆𝜃=180 𝜋 rad
D
∆𝜃=220 𝜋 rad
االتسارع الزاوي
االتسارع الزاوية المتوسط : وهي عبارة عن معدل السرعة الزاوية ويرمز لها بالرمز \[ 𝛼\]\[{{𝛼}_\text{avg}} = \frac{W_2 - W_1}{t_2-t_1}\] وتقدر بوحدة \[\frac{rad}{S^2}\] التسارع الزاوي للحركة الدائرية تحدث عندما يتحرك الجسم حركة دائرية بسرعة غير ثابتة
التجربة 2 قياس التسارع الزاوي
اجعل الحركة الدائرية غير منتظمة
( a𝛾 ≠ 0 ) حرك ايقونة التسارع الزاوي واجعل قيمة للتسارع الزاوي لا تساوي الصفر
( w-t )اضغط على الخط البياني
الفترة الزمنية
السرعة الزاوية النهائية
السرعة الزاوية الإبتدئية
\[t_2 -t_1= ....s\]
\[w_2= .....rad\]
\[w_1= ....rad\]
التسارع الزاوي
\[𝛼 =a𝛾= \frac{w_2 - w_1}{t_2 -t_1}= ......\frac{rad}{s^2} \] متوسط التسارع الزاوية معدل تغير سرعة الزاوية خلال الزمن
إذا كان لدينا جسم يتحرك بمسار دائري وبسرعة متغيرة هناك تسارع زاوي وبالتالي تسارع خط
\[3 \star\star\]
دولاب سيارة يتحرك بسرعة زاوية \[W=10 \frac{rad}{s}\] غير سرعته فأصبحت \[W=15 \frac{rad}{s} \] خلال زمن قدرة \[t=10\;s\] فإن التسارع الزاوي للدولاب يعادل
أختر الإجابة الصحيحة
A
𝛼=4 𝑟𝑎𝑑/𝑠2
B
𝛼=2 𝑟𝑎𝑑/𝑠2
C
𝛼=1 𝑟𝑎𝑑/𝑠2
D
𝛼=0.5 𝑟𝑎𝑑/𝑠2
نتائج مهمة :العلاقة بين الحركة الخطية والحركة الدائرية
في الحركة الخطية يقطع الجسم إزاحة خطية \[s\] بينما في الحركة الدائرية يقطع الجسم إزاحة زاوية \[ 𝜃\]
في الحركة الخطية يتحرك الجسم بسرعة خطية \[𝜗\] بينما في الحركة الدائرية يتحرك الجسم بسرعة زاوية \[W\]
في الحركة الخطية يتحرك الجسم بعجلة خطية \[a\] بينما في الحركة الدائرية يتحرك الجسم بعجلة زاوية \[𝛼\]
عزم قوة
نقول أن قوة لها عزم اذا كانت القوة قادرة على احداث حركة دورانية لجسم حول محور الدوران.
وهو قيمة متجهة لقياس مدى قدرة قوة على تدوير الجسم حول محور ما، على أنه حاصل ضرب القوة بطول الذراع ويدعى العزم
يرمز لعزم الدوران بالحرف الإغريقي "تاو" ووحدته في النظام الدولي للوحدات هي نيوتن متر
\[\vec{𝜏}=\vec r×\vec F=r.F .𝑆𝑖𝑛 {𝜃 }\]
باستطاعتنا باستخدام قاعدة اليد اليمنى لإيجاد اتجاه متجه عزم الدوران. إذا وضعنا أصابعنا في اتجاه الذراع، وقمنا بلفها باتجاه القوة ، سيشير الإبهام باتجاه مُتجه عزم الدوران
4
في الشكل أدناه قوتين متساويتين أثرت على جسم قابل للدوران فأصبح الجسم يدور فإن أحد الاجابات التالية صحيحة
أختر الإجابة الصحيحة
A
𝜏𝐵 > 𝜏𝐴
B
𝜏𝐴 = 𝜏𝐵
C
𝜏𝐴 > 𝜏𝐵
D
لا يوجد إجابة صحيحة
محصلة العزوم
قد يكون هناك أكثر من قوة واحدة تؤثر على جسم ما، كل واحدة من هذه القوى قد تؤثر على الجسم من نقاط مختلفة. ثم إن كل قوة من هذه القوى ستولد عزم دوران على الجسم، ويكون عزم الدوران الكلي مجموع عزوم الدوران الفردية.
ويكون اتجاة الدوران باتجاه العزم الأكبر
مثال محصلة العزوم
أوجد محصلة العزم , الجسم متأثر بقوتين وقابل للدوران حول محور يقع في مركز الجسم
F1 = F2 =50. N
r1 = 30 cm, r2 = 50 cm
القوة الأولى مقدارها 50 نيوتن وتبعد 30 سانتي متر عن محور الدوران والقوه تصنع زاوية 90 درجة مع الذراع وتجعل الجسم يدور عكس عقارب الساعة فإن عزمها موجب.
\[𝜏_1=𝑟_1.𝐹_1 .𝑆𝑖𝑛 {𝜃_1 }=+0.3×50 ×𝑆𝑖𝑛 {90 }= +15 N.m\]
القوة الثانية مقدارها 50 نيوتن وتبعد 50 سانتي متر عن محور الدوران والقوه تصنع زاوية 60 درجة مع الذراع وتجعل الجسم يدور مع عقارب الساعة فإن عزمها سالب.
\[𝜏_2=𝑟_2.𝐹_2 .𝑆𝑖𝑛 {𝜃_2 }=-0.5×50 ×𝑆𝑖𝑛 {60 }= -21.65 N.m\]
حساب محصلة العزم الكلي \[𝜏_{net}=𝜏_1+𝜏_2=+15-21.65=-6.65 N.m\] الإشارة السالبة تدل على أن الجسم سوف يدور في النهاية مع عقارب الساعة
ملاحظة مهمة
متى ينعدم عزم الدوران لجسم
لاحظ أي قوة تمر بمحور الدوران أو توازي محور الدوران فإن عزمها معدوم
في هذه المحاكاة يوجد أوزان مختلفة على لعبة الميزان لكل منهما عزم دوران
أكمل بيانات الجدول وفي كل مره طبق على التجربة للتأكد من النتائج
محصلة العزوم \[𝜏_{net}=𝜏_1+𝜏_0\]
عزم الدوران القوة على يسار الوتد \[𝜏_0=𝑟_0.𝐹_0 .𝑆𝑖𝑛 {90 }\]
عزم الدوران القوة على يمين الوتد \[𝜏_1=𝑟_1.𝐹_1 .𝑆𝑖𝑛 {90 }\]
\[𝜏_{net}=........\]
\[m_1=5 Kg,r_1=10m\]\[................\]
\[m_2=8 Kg,r_1=6m\]\[................\]
\[𝜏_{net}=........\]
\[m_1=7 Kg,r_1=3m\]\[................\]
\[m_2=9 Kg,r_2=3m\]\[................\]
\[𝜏_{net}=........\]
\[m_1=3 Kg,r_1=8m\]\[................\]
\[m_2=8 Kg,r_2=3m\]\[................\]
\[𝜏_{net}=........\]
\[m_1=5 Kg,r_1=10m\]\[................\]
\[m_2=2 Kg,r_1=2m\]\[................\]
مركز الكتلة
مركز الكتلة : هو نقطة على الجسم تتركز فيها كتلة هذا الجسم كلها
إذا خضع جسم صلب لقوى متوازنة، توجد دوماً نقطة وحيدة من الجسم تكون حركتها مستقيمة منتظمة. تسمى هذه النقطة مركز ثقل الجسم
متى يكون الجسم أكثر اتزان واستقرار
في هذه المحاكاة يتم الضغط على الأيقونة الموجودة بجوار كل جسم للتغير من القاعدة وبعد المركز ونغير من ميل المستوي عن طريق المجرى الموجود على اليسار حتى تصبح قوة الوزن قادرة على تدوير وقلب الجسم
لاحظ ماذا يحدث كلما كانت قاعدة الجسم أكبر ومركز الكتلة قريب للقاعدة ماذا يحدث
تجربة استقرار جسم
الاتزان الدوراني
متى يكون الجسم في حالة اتزان دوراني
ليتحقق الاتزان لابد من توافر شرطيين أساسيين وهما
أن تكون محصلة عزوم القوى تساوي صفر ويسمى الاتزان الدوراني
أن تكون محصلة القوى المؤثرة على الجسم تساوي صفر ويسمى الاتزان الانتقالي
في هذه المحاكاة علق كتل مختلفة وبأبعاد مختلفة عن محور الدوران محققاً الأتزان الدوراني وتأكد من خلال النتائج
في هذه المحاكاة توقع إمكانية استخدام كائنات مختلفة لإنشاء توازن اللوح الخشبي.
توقع كيفية تغيير موضع الأشياء على السبورة للتأثير على حركة اللوحة.
اكتب القواعد التي تتنبأ بأي جانب من الكائن سوف يميل عند وضعه على السبورة.
استخدم القواعد الخاصة بك لحل الألغاز المتعلقة بالتوازن
المصدر
https://ophysics.com/em4.html
Rotational Motion
Angular Displacement
Remember: Linear displacement = Final position – Initial position
\[∆X=X_2−X_1\]
Angular displacement = Final angle – Initial angle
\[∆𝜃=𝜃_2−𝜃_1\]
If an object moves from one point to another and cuts an arc of length \[S\] on the circumference of a circle of radius \[r\], then the angle opposite the arc is called the angular displacement and is denoted by the symbol \[𝜃\]
\[𝜃 =\frac{s}{r}\]
Angular displacement is a vector quantity. If the rotation is counterclockwise, it takes a positive sign, and if the rotation is clockwise, it takes a negative sign.
The radian represents the unit for measuring angular coordinates
(rev) You may find angular displacement in degrees or revolutions
The angle is converted to radians according to the following conversion factors
Conversion factor from revolutions to radians
Conversion factor from degrees to radians
\[2𝜋 (rad)= 1 rev\]
\[𝜋 (rad )= 180^0\]
Example: An object moving in circular motion cuts an angular displacement of 2.25 revolutions. How much is that in radians?
Example: An object cuts an angular displacement of 120 degrees. How much is that in radians?
\[ 𝜃 = 2.25 × 2𝜋 =14.13 rad \]
\[ 𝜃 = 120 ^0 × \frac{𝜋}{180}=2.1 rad \]
Angular Velocity
Remember: The linear velocity of an object is the change in the linear coordinates of the object with respect to time
Angular velocity of an object: is the change in the angular coordinate of the object with time \[W_{avg}=\frac{∆𝜃 (rad)}{∆t (s)}= \frac{𝜃_2 - 𝜃_1}{t_2 -t_1}\]
Experiment 1: Measuring Angular Velocity
Angular velocity of an object: is the change in the angular coordinate of the object with time
( a𝛾=0.0 ) Make the circular motion uniform
( 𝜃-t ) Click on the graph
Time period
Final angular displacement
Initial angular displacement
\[t_2 -t_1= ....s\]
\[𝜃_2= .....rad\]
\[𝜃_1= ....rad\]
Angular velocity
Direction of angular velocity
\[W= \frac{𝜃_2 - 𝜃_1}{t_2 -t_1}= ......rad/s\] Angular velocity is the rate of change of angle over time
If rotation is counterclockwise
If rotation is clockwise
\[1 \star\]
An object moves in uniform circular motion so that it makes one revolution every second. Its angular velocity in \[rad/s\] is:
Choose the correct answer
A
w= 4𝜋 rad/s
B
w= 𝜋 rad/s
C
w= 2𝜋 rad/s
D
w= 3𝜋 rad/s
\[2 \star\]
A fan rotates with angular velocity of
(60 𝜋 rad/s)
The angle covered by one of its blades in time \[t=3 \;s \] equals:
Choose the correct answer
A
∆𝜃=120 𝜋 rad
B
∆𝜃=60 𝜋 rad
C
∆𝜃=180 𝜋 rad
D
∆𝜃=220 𝜋 rad
Angular Acceleration
Average angular acceleration: It is the rate of change of angular velocity and is denoted by the symbol \[ 𝛼\]\[{{𝛼}_\text{avg}} = \frac{W_2 - W_1}{t_2-t_1}\] and is measured in units of \[\frac{rad}{S^2}\] Angular acceleration in circular motion occurs when an object moves in circular motion with non-constant velocity
Experiment 2: Measuring Angular Acceleration
Make the circular motion non-uniform
( a𝛾 ≠ 0 ) Move the angular acceleration icon and set a value for angular acceleration not equal to zero
( w-t ) Click on the graph
Time period
Final angular velocity
Initial angular velocity
\[t_2 -t_1= ....s\]
\[w_2= .....rad\]
\[w_1= ....rad\]
Angular acceleration
\[𝛼 =a𝛾= \frac{w_2 - w_1}{t_2 -t_1}= ......\frac{rad}{s^2} \] Average angular acceleration is the rate of change of angular velocity over time
If we have an object moving in a circular path with variable speed, there is angular acceleration and therefore linear acceleration
\[3 \star\star\]
A car wheel moves with angular velocity \[W=10 \frac{rad}{s}\] and changes its speed to become \[W=15 \frac{rad}{s} \] over a time of \[t=10\;s\]. The angular acceleration of the wheel equals:
Choose the correct answer
A
𝛼=4 𝑟𝑎𝑑/𝑠2
B
𝛼=2 𝑟𝑎𝑑/𝑠2
C
𝛼=1 𝑟𝑎𝑑/𝑠2
D
𝛼=0.5 𝑟𝑎𝑑/𝑠2
Important Results: Relationship between Linear Motion and Circular Motion
In linear motion, the object covers a linear displacement \[s\] while in circular motion, the object covers an angular displacement \[ 𝜃\]
In linear motion, the object moves with linear velocity \[𝜗\] while in circular motion, the object moves with angular velocity \[W\]
In linear motion, the object moves with linear acceleration \[a\] while in circular motion, the object moves with angular acceleration \[𝛼\]
Torque
We say that a force has torque if the force is capable of causing rotational motion of an object around an axis of rotation.
It is a vector quantity that measures the ability of a force to rotate an object around an axis, defined as the product of the force and the lever arm length, and is called torque
Torque is denoted by the Greek letter "tau" and its unit in the International System of Units is Newton meter
\[\vec{𝜏}=\vec r×\vec F=r.F .𝑆𝑖𝑛 {𝜃 }\]
We can use the right-hand rule to find the direction of the torque vector. If we place our fingers in the direction of the lever arm, and curl them in the direction of the force, the thumb will point in the direction of the torque vector
4
In the figure below, two equal forces acted on a rotatable object and the object started rotating. One of the following answers is correct:
Choose the correct answer
A
𝜏𝐵 > 𝜏𝐴
B
𝜏𝐴 = 𝜏𝐵
C
𝜏𝐴 > 𝜏𝐵
D
No correct answer
Net Torque
There may be more than one force acting on an object, each of these forces may act on the object from different points. Then each of these forces will generate a torque on the object, and the total torque will be the sum of the individual torques.
The direction of rotation is in the direction of the larger torque
Example of net torque
Find the net torque, the object is affected by two forces and can rotate around an axis located at the center of the object
F1 = F2 =50. N
r1 = 30 cm, r2 = 50 cm
The first force has a magnitude of 50 Newtons and is 30 centimeters away from the axis of rotation. The force makes a 90-degree angle with the lever arm and causes the object to rotate counterclockwise, so its torque is positive.
\[𝜏_1=𝑟_1.𝐹_1 .𝑆𝑖𝑛 {𝜃_1 }=+0.3×50 ×𝑆𝑖𝑛 {90 }= +15 N.m\]
The second force has a magnitude of 50 Newtons and is 50 centimeters away from the axis of rotation. The force makes a 60-degree angle with the lever arm and causes the object to rotate clockwise, so its torque is negative.
\[𝜏_2=𝑟_2.𝐹_2 .𝑆𝑖𝑛 {𝜃_2 }=-0.5×50 ×𝑆𝑖𝑛 {60 }= -21.65 N.m\]
Calculation of the net torque \[𝜏_{net}=𝜏_1+𝜏_2=+15-21.65=-6.65 N.m\] The negative sign indicates that the object will eventually rotate clockwise
Important note
When does the torque on an object become zero?
Note that any force that passes through the axis of rotation or is parallel to the axis of rotation has zero torque
In this simulation, there are different weights on a balance game, each with its own torque
Complete the table data and each time apply it to the experiment to verify the results
Net torque \[𝜏_{net}=𝜏_1+𝜏_0\]
Torque of force on left side \[𝜏_0=𝑟_0.𝐹_0 .𝑆𝑖𝑛 {90 }\]
Torque of force on right side \[𝜏_1=𝑟_1.𝐹_1 .𝑆𝑖𝑛 {90 }\]
\[𝜏_{net}=........\]
\[m_1=5 Kg,r_1=10m\]\[................\]
\[m_2=8 Kg,r_1=6m\]\[................\]
\[𝜏_{net}=........\]
\[m_1=7 Kg,r_1=3m\]\[................\]
\[m_2=9 Kg,r_2=3m\]\[................\]
\[𝜏_{net}=........\]
\[m_1=3 Kg,r_1=8m\]\[................\]
\[m_2=8 Kg,r_2=3m\]\[................\]
\[𝜏_{net}=........\]
\[m_1=5 Kg,r_1=10m\]\[................\]
\[m_2=2 Kg,r_1=2m\]\[................\]
Center of Mass
Center of mass: It is a point on the object where the entire mass of this object is concentrated
If a rigid body is subjected to balanced forces, there is always a single point of the body whose motion is straight and uniform. This point is called the center of gravity of the body
When is an object more balanced and stable?
In this simulation, click on the icon next to each object to change the base and center, and change the slope of the plane using the slider on the left until the weight force is able to rotate and tip the object
Notice what happens when the object's base is larger and the center of mass is close to the base. What happens?
Object Stability Experiment
Rotational Equilibrium
When is an object in rotational equilibrium?
For equilibrium to be achieved, two basic conditions must be met:
The net torque of the forces must equal zero, which is called rotational equilibrium
The net force acting on the object must equal zero, which is called translational equilibrium
In this simulation, hang different masses at different distances from the axis of rotation to achieve rotational equilibrium and verify through the results
In this simulation, predict the possibility of using different objects to create balance on the wooden board.
Predict how changing the position of objects on the board will affect the movement of the board.
Write rules that predict which side of the object will tilt when placed on the board.
Use your rules to solve balance-related puzzles
Source
https://ophysics.com/em4.html
الحركة الدورانية |
إذا تحرك جسم من نقطة الى اخرى وقطع قوس طوله \[S\] على محيط دائره نصف قطرها \[r\] فإن الزاويه التي تقابل القوس تسمى بالازاحه الزاويه ويرمز لها بالرمز \[𝜃\]
\[𝜃 =\frac{s}{r}\]
الإزاحة الزاوية كمية متجهه إذا كان الدوران عكس عقارب الساعة تأخذ إشارة موجبة وإذا كان الدوران مع عقارب الساعة تأخذ إشارة سالبة
يمثل الراديان الوحدة لقياس الإحداثيات الزاوية
(rev) قد تجد الإزاحة الزاوية بوحدة الدرجات او بوحدة الدورات
يتم تحويل الزاوية إلى الراديان حسب معاملات التحويل التالية
معامل التحويل من الدورات إلى الراديان |
معامل التحويل من الدرجات إلى الراديان |
\[2𝜋 (rad)= 1 rev\] |
\[𝜋 (rad )= 180^0\] |
مثال :جسم يتحرك حركة دائرية قطع إزاحة زاوية قدرها 2.25 دورة فكم يعادل بالراديان |
مثال : جسم قطع إزاحة زاوية 120 درجة فكم يعادل بوحدة الراديان |
\[ 𝜃 = 2.25 × 2𝜋 =14.13 rad \] |
\[ 𝜃 = 120 ^0 × \frac{𝜋}{180}=2.1 rad \] |
تذكر : السرعة المتجهة الخطية لجسم ما هي تغير الإحداثيات الخطية للجسم بالنسبة للزمن
السرعة الزاوية لجسم ما : هي تغير الإحداثي الزاوي للجسم مع الزمن \[W_{avg}=\frac{∆𝜃 (rad)}{∆t (s)}= \frac{𝜃_2 - 𝜃_1}{t_2 -t_1}\]
التجربة 1 قياس السرعة الزاوية
السرعة الزاوية لجسم ما : هي تغير الإحداثي الزاوي للجسم مع الزمن
( a𝛾=0.0 )اجعل الحركة الدائرية منتظمة
( 𝜃-t )اضغط على الخط البياني
الفترة الزمنية |
الإزاحة الزاوية النهائية |
الإزاحة الزاوية الإبتدئية |
\[t_2 -t_1= ....s\] |
\[𝜃_2= .....rad\] |
\[𝜃_1= ....rad\] |
السرعة الزاوية |
اتجاه السرعة الزاوية |
\[W= \frac{𝜃_2 - 𝜃_1}{t_2 -t_1}= ......rad/s\] السرعة الزاوية معدل تغير الزاوية خلال الزمن |
|
يتحرك جسم حركه دائريه منتظمة بحيث يعمل دوره واحده كل ثانيه فان سرعته الزاوية بوحدة \[rad/s\]
أختر الإجابة الصحيحة
اضغط هنا تظهر طريقة الحل
مروحه تدور بسرعه بزاويه قدرها
(60 𝜋 rad/s)
فان الزاوية التي تقطعها أحد شفراتها خلال زمن قدره \[t=3 \;s \] تعادل
أختر الإجابة الصحيحة
االتسارع الزاوية المتوسط : وهي عبارة عن معدل السرعة الزاوية ويرمز لها بالرمز \[ 𝛼\]\[{{𝛼}_\text{avg}} = \frac{W_2 - W_1}{t_2-t_1}\] وتقدر بوحدة \[\frac{rad}{S^2}\] التسارع الزاوي للحركة الدائرية تحدث عندما يتحرك الجسم حركة دائرية بسرعة غير ثابتة
التجربة 2 قياس التسارع الزاوي
اجعل الحركة الدائرية غير منتظمة
( a𝛾 ≠ 0 ) حرك ايقونة التسارع الزاوي واجعل قيمة للتسارع الزاوي لا تساوي الصفر
( w-t )اضغط على الخط البياني
الفترة الزمنية |
السرعة الزاوية النهائية |
السرعة الزاوية الإبتدئية |
\[t_2 -t_1= ....s\] |
\[w_2= .....rad\] |
\[w_1= ....rad\] |
التسارع الزاوي |
\[𝛼 =a𝛾= \frac{w_2 - w_1}{t_2 -t_1}= ......\frac{rad}{s^2} \] متوسط التسارع الزاوية معدل تغير سرعة الزاوية خلال الزمن |
إذا كان لدينا جسم يتحرك بمسار دائري وبسرعة متغيرة هناك تسارع زاوي وبالتالي تسارع خط \[3 \star\star\]
دولاب سيارة يتحرك بسرعة زاوية \[W=10 \frac{rad}{s}\] غير سرعته فأصبحت \[W=15 \frac{rad}{s} \] خلال زمن قدرة \[t=10\;s\] فإن التسارع الزاوي للدولاب يعادل
أختر الإجابة الصحيحة
في الحركة الخطية يقطع الجسم إزاحة خطية \[s\] بينما في الحركة الدائرية يقطع الجسم إزاحة زاوية \[ 𝜃\]
في الحركة الخطية يتحرك الجسم بسرعة خطية \[𝜗\] بينما في الحركة الدائرية يتحرك الجسم بسرعة زاوية \[W\]
في الحركة الخطية يتحرك الجسم بعجلة خطية \[a\] بينما في الحركة الدائرية يتحرك الجسم بعجلة زاوية \[𝛼\]
نقول أن قوة لها عزم اذا كانت القوة قادرة على احداث حركة دورانية لجسم حول محور الدوران.
وهو قيمة متجهة لقياس مدى قدرة قوة على تدوير الجسم حول محور ما، على أنه حاصل ضرب القوة بطول الذراع ويدعى العزم
يرمز لعزم الدوران بالحرف الإغريقي "تاو" ووحدته في النظام الدولي للوحدات هي نيوتن متر
\[\vec{𝜏}=\vec r×\vec F=r.F .𝑆𝑖𝑛 {𝜃 }\]
باستطاعتنا باستخدام قاعدة اليد اليمنى لإيجاد اتجاه متجه عزم الدوران. إذا وضعنا أصابعنا في اتجاه الذراع، وقمنا بلفها باتجاه القوة ، سيشير الإبهام باتجاه مُتجه عزم الدوران
4
في الشكل أدناه قوتين متساويتين أثرت على جسم قابل للدوران فأصبح الجسم يدور فإن أحد الاجابات التالية صحيحة
أختر الإجابة الصحيحة
محصلة العزوم
قد يكون هناك أكثر من قوة واحدة تؤثر على جسم ما، كل واحدة من هذه القوى قد تؤثر على الجسم من نقاط مختلفة. ثم إن كل قوة من هذه القوى ستولد عزم دوران على الجسم، ويكون عزم الدوران الكلي مجموع عزوم الدوران الفردية.
ويكون اتجاة الدوران باتجاه العزم الأكبر
مثال محصلة العزوم
أوجد محصلة العزم , الجسم متأثر بقوتين وقابل للدوران حول محور يقع في مركز الجسم
F1 = F2 =50. N
r1 = 30 cm, r2 = 50 cm
القوة الأولى مقدارها 50 نيوتن وتبعد 30 سانتي متر عن محور الدوران والقوه تصنع زاوية 90 درجة مع الذراع وتجعل الجسم يدور عكس عقارب الساعة فإن عزمها موجب.
\[𝜏_1=𝑟_1.𝐹_1 .𝑆𝑖𝑛 {𝜃_1 }=+0.3×50 ×𝑆𝑖𝑛 {90 }= +15 N.m\]
القوة الثانية مقدارها 50 نيوتن وتبعد 50 سانتي متر عن محور الدوران والقوه تصنع زاوية 60 درجة مع الذراع وتجعل الجسم يدور مع عقارب الساعة فإن عزمها سالب.
\[𝜏_2=𝑟_2.𝐹_2 .𝑆𝑖𝑛 {𝜃_2 }=-0.5×50 ×𝑆𝑖𝑛 {60 }= -21.65 N.m\]
حساب محصلة العزم الكلي \[𝜏_{net}=𝜏_1+𝜏_2=+15-21.65=-6.65 N.m\] الإشارة السالبة تدل على أن الجسم سوف يدور في النهاية مع عقارب الساعة
ملاحظة مهمة
متى ينعدم عزم الدوران لجسم
لاحظ أي قوة تمر بمحور الدوران أو توازي محور الدوران فإن عزمها معدوم
في هذه المحاكاة يوجد أوزان مختلفة على لعبة الميزان لكل منهما عزم دوران
محصلة العزوم \[𝜏_{net}=𝜏_1+𝜏_0\] |
عزم الدوران القوة على يسار الوتد \[𝜏_0=𝑟_0.𝐹_0 .𝑆𝑖𝑛 {90 }\] |
عزم الدوران القوة على يمين الوتد \[𝜏_1=𝑟_1.𝐹_1 .𝑆𝑖𝑛 {90 }\] |
\[𝜏_{net}=........\] |
\[m_1=5 Kg,r_1=10m\]\[................\] |
\[m_2=8 Kg,r_1=6m\]\[................\] |
\[𝜏_{net}=........\] |
\[m_1=7 Kg,r_1=3m\]\[................\] |
\[m_2=9 Kg,r_2=3m\]\[................\] |
\[𝜏_{net}=........\] |
\[m_1=3 Kg,r_1=8m\]\[................\] |
\[m_2=8 Kg,r_2=3m\]\[................\] |
\[𝜏_{net}=........\] |
\[m_1=5 Kg,r_1=10m\]\[................\] |
\[m_2=2 Kg,r_1=2m\]\[................\] |
مركز الكتلة : هو نقطة على الجسم تتركز فيها كتلة هذا الجسم كلها
إذا خضع جسم صلب لقوى متوازنة، توجد دوماً نقطة وحيدة من الجسم تكون حركتها مستقيمة منتظمة. تسمى هذه النقطة مركز ثقل الجسم
متى يكون الجسم أكثر اتزان واستقرار
في هذه المحاكاة يتم الضغط على الأيقونة الموجودة بجوار كل جسم للتغير من القاعدة وبعد المركز ونغير من ميل المستوي عن طريق المجرى الموجود على اليسار حتى تصبح قوة الوزن قادرة على تدوير وقلب الجسم
لاحظ ماذا يحدث كلما كانت قاعدة الجسم أكبر ومركز الكتلة قريب للقاعدة ماذا يحدث
الاتزان الدوراني
متى يكون الجسم في حالة اتزان دوراني
ليتحقق الاتزان لابد من توافر شرطيين أساسيين وهما
أن تكون محصلة عزوم القوى تساوي صفر ويسمى الاتزان الدوراني
أن تكون محصلة القوى المؤثرة على الجسم تساوي صفر ويسمى الاتزان الانتقالي
في هذه المحاكاة علق كتل مختلفة وبأبعاد مختلفة عن محور الدوران محققاً الأتزان الدوراني وتأكد من خلال النتائج
في هذه المحاكاة توقع إمكانية استخدام كائنات مختلفة لإنشاء توازن اللوح الخشبي.
توقع كيفية تغيير موضع الأشياء على السبورة للتأثير على حركة اللوحة.
اكتب القواعد التي تتنبأ بأي جانب من الكائن سوف يميل عند وضعه على السبورة.
استخدم القواعد الخاصة بك لحل الألغاز المتعلقة بالتوازن
https://ophysics.com/em4.html
Rotational Motion |
If an object moves from one point to another and cuts an arc of length \[S\] on the circumference of a circle of radius \[r\], then the angle opposite the arc is called the angular displacement and is denoted by the symbol \[𝜃\]
\[𝜃 =\frac{s}{r}\]
Angular displacement is a vector quantity. If the rotation is counterclockwise, it takes a positive sign, and if the rotation is clockwise, it takes a negative sign.
The radian represents the unit for measuring angular coordinates
(rev) You may find angular displacement in degrees or revolutions
The angle is converted to radians according to the following conversion factors
Conversion factor from revolutions to radians |
Conversion factor from degrees to radians |
\[2𝜋 (rad)= 1 rev\] |
\[𝜋 (rad )= 180^0\] |
Example: An object moving in circular motion cuts an angular displacement of 2.25 revolutions. How much is that in radians? |
Example: An object cuts an angular displacement of 120 degrees. How much is that in radians? |
\[ 𝜃 = 2.25 × 2𝜋 =14.13 rad \] |
\[ 𝜃 = 120 ^0 × \frac{𝜋}{180}=2.1 rad \] |
Remember: The linear velocity of an object is the change in the linear coordinates of the object with respect to time
Angular velocity of an object: is the change in the angular coordinate of the object with time \[W_{avg}=\frac{∆𝜃 (rad)}{∆t (s)}= \frac{𝜃_2 - 𝜃_1}{t_2 -t_1}\]
Experiment 1: Measuring Angular Velocity
Angular velocity of an object: is the change in the angular coordinate of the object with time
( a𝛾=0.0 ) Make the circular motion uniform
( 𝜃-t ) Click on the graph
Time period |
Final angular displacement |
Initial angular displacement |
\[t_2 -t_1= ....s\] |
\[𝜃_2= .....rad\] |
\[𝜃_1= ....rad\] |
Angular velocity |
Direction of angular velocity |
\[W= \frac{𝜃_2 - 𝜃_1}{t_2 -t_1}= ......rad/s\] Angular velocity is the rate of change of angle over time |
|
An object moves in uniform circular motion so that it makes one revolution every second. Its angular velocity in \[rad/s\] is:
Choose the correct answer
A fan rotates with angular velocity of
(60 𝜋 rad/s)
The angle covered by one of its blades in time \[t=3 \;s \] equals:
Choose the correct answer
Average angular acceleration: It is the rate of change of angular velocity and is denoted by the symbol \[ 𝛼\]\[{{𝛼}_\text{avg}} = \frac{W_2 - W_1}{t_2-t_1}\] and is measured in units of \[\frac{rad}{S^2}\] Angular acceleration in circular motion occurs when an object moves in circular motion with non-constant velocity
Experiment 2: Measuring Angular Acceleration
Make the circular motion non-uniform
( a𝛾 ≠ 0 ) Move the angular acceleration icon and set a value for angular acceleration not equal to zero
( w-t ) Click on the graph
Time period |
Final angular velocity |
Initial angular velocity |
\[t_2 -t_1= ....s\] |
\[w_2= .....rad\] |
\[w_1= ....rad\] |
Angular acceleration |
\[𝛼 =a𝛾= \frac{w_2 - w_1}{t_2 -t_1}= ......\frac{rad}{s^2} \] Average angular acceleration is the rate of change of angular velocity over time |
If we have an object moving in a circular path with variable speed, there is angular acceleration and therefore linear acceleration \[3 \star\star\]
A car wheel moves with angular velocity \[W=10 \frac{rad}{s}\] and changes its speed to become \[W=15 \frac{rad}{s} \] over a time of \[t=10\;s\]. The angular acceleration of the wheel equals:
Choose the correct answer
In linear motion, the object covers a linear displacement \[s\] while in circular motion, the object covers an angular displacement \[ 𝜃\]
In linear motion, the object moves with linear velocity \[𝜗\] while in circular motion, the object moves with angular velocity \[W\]
In linear motion, the object moves with linear acceleration \[a\] while in circular motion, the object moves with angular acceleration \[𝛼\]
We say that a force has torque if the force is capable of causing rotational motion of an object around an axis of rotation.
It is a vector quantity that measures the ability of a force to rotate an object around an axis, defined as the product of the force and the lever arm length, and is called torque
Torque is denoted by the Greek letter "tau" and its unit in the International System of Units is Newton meter
\[\vec{𝜏}=\vec r×\vec F=r.F .𝑆𝑖𝑛 {𝜃 }\]
We can use the right-hand rule to find the direction of the torque vector. If we place our fingers in the direction of the lever arm, and curl them in the direction of the force, the thumb will point in the direction of the torque vector
4
In the figure below, two equal forces acted on a rotatable object and the object started rotating. One of the following answers is correct:
Choose the correct answer
Net Torque
There may be more than one force acting on an object, each of these forces may act on the object from different points. Then each of these forces will generate a torque on the object, and the total torque will be the sum of the individual torques.
The direction of rotation is in the direction of the larger torque
Example of net torque
Find the net torque, the object is affected by two forces and can rotate around an axis located at the center of the object
F1 = F2 =50. N
r1 = 30 cm, r2 = 50 cm
The first force has a magnitude of 50 Newtons and is 30 centimeters away from the axis of rotation. The force makes a 90-degree angle with the lever arm and causes the object to rotate counterclockwise, so its torque is positive.
\[𝜏_1=𝑟_1.𝐹_1 .𝑆𝑖𝑛 {𝜃_1 }=+0.3×50 ×𝑆𝑖𝑛 {90 }= +15 N.m\]
The second force has a magnitude of 50 Newtons and is 50 centimeters away from the axis of rotation. The force makes a 60-degree angle with the lever arm and causes the object to rotate clockwise, so its torque is negative.
\[𝜏_2=𝑟_2.𝐹_2 .𝑆𝑖𝑛 {𝜃_2 }=-0.5×50 ×𝑆𝑖𝑛 {60 }= -21.65 N.m\]
Calculation of the net torque \[𝜏_{net}=𝜏_1+𝜏_2=+15-21.65=-6.65 N.m\] The negative sign indicates that the object will eventually rotate clockwise
Important note
When does the torque on an object become zero?
Note that any force that passes through the axis of rotation or is parallel to the axis of rotation has zero torque
In this simulation, there are different weights on a balance game, each with its own torque
Net torque \[𝜏_{net}=𝜏_1+𝜏_0\] |
Torque of force on left side \[𝜏_0=𝑟_0.𝐹_0 .𝑆𝑖𝑛 {90 }\] |
Torque of force on right side \[𝜏_1=𝑟_1.𝐹_1 .𝑆𝑖𝑛 {90 }\] |
\[𝜏_{net}=........\] |
\[m_1=5 Kg,r_1=10m\]\[................\] |
\[m_2=8 Kg,r_1=6m\]\[................\] |
\[𝜏_{net}=........\] |
\[m_1=7 Kg,r_1=3m\]\[................\] |
\[m_2=9 Kg,r_2=3m\]\[................\] |
\[𝜏_{net}=........\] |
\[m_1=3 Kg,r_1=8m\]\[................\] |
\[m_2=8 Kg,r_2=3m\]\[................\] |
\[𝜏_{net}=........\] |
\[m_1=5 Kg,r_1=10m\]\[................\] |
\[m_2=2 Kg,r_1=2m\]\[................\] |
Center of mass: It is a point on the object where the entire mass of this object is concentrated
If a rigid body is subjected to balanced forces, there is always a single point of the body whose motion is straight and uniform. This point is called the center of gravity of the body
When is an object more balanced and stable?
In this simulation, click on the icon next to each object to change the base and center, and change the slope of the plane using the slider on the left until the weight force is able to rotate and tip the object
Notice what happens when the object's base is larger and the center of mass is close to the base. What happens?
Rotational Equilibrium
When is an object in rotational equilibrium?
For equilibrium to be achieved, two basic conditions must be met:
The net torque of the forces must equal zero, which is called rotational equilibrium
The net force acting on the object must equal zero, which is called translational equilibrium
In this simulation, hang different masses at different distances from the axis of rotation to achieve rotational equilibrium and verify through the results
In this simulation, predict the possibility of using different objects to create balance on the wooden board.
Predict how changing the position of objects on the board will affect the movement of the board.
Write rules that predict which side of the object will tilt when placed on the board.
Use your rules to solve balance-related puzzles
https://ophysics.com/em4.html
No comments:
Post a Comment