📄 اطبع pdf
00971504825082

<<<انكسار الضوء وقانون سنل >>>

الإنكسار

معامل الانكسار ：
زاوية السقوط ：

30

°　


"انكسار الضوء : هو تغير اتجاه انتشار الموجة عندما تنتقل الموجة من وسط إلى أخر

عندما يحدث الإنكسار تتغير سرعة الموجة

طول الموجة يتغير عندما يحدث الإنكسار

والمصدر واحد للأمواج الساقطة والمنكسرة أي التردد ثابت

(..............) الشعاع الساقط يمثل الرقم

(..............) الشعاع المنكسر يمثل الرقم

(..............) زاوية السقوط يمثل الرقم

(..............) زاوية الإنكسار يمثل الرقم

(..............) العمود على السطح يمثل الرقم

(..............) السطح الفاصل يمثل الرقم

السؤال متى ينكسر الضوء مقتربا من العمود
متى ينكسر مبتعدا عن العمود
ومتى لا يحدث انكسار

سقوط الضوء من وسط ذو سرعة أكبر إلى وسط ذو سرعة أقل
غير زاوية السقوط من المؤشر ولاحظ النتائج

سقوط الضوء من وسط ذو سرعة أقل إلى وسط ذو سرعة أكبر
غير زاوية السقوط من المؤشر ولاحظ النتائج


غير زاوية السقوط من المؤشر ولاحظ النتائج

نتائج مهمة

إذا انتقل الضوء من وسط سرعته أكبر الى وسط سرعته أقل ينكسر مقتربا من عمود الإنكسار

إذا انتقل الضوء من وسط سرعته أقل الى وسط سرعته أكبر ينكسر مبتعدا من عمود الإنكسار

لا يحدث انكسار إذا سقط الضوء عمودي على السطح الفاصل

لا يحدث انكسار إذا سقط الضوء بنفس الوسط

قانون سنل في الانكسار

وقد وجد سنل في عام 1621 أنه عند مرور الضوء من وسط شفاف الى وسط شفاف أخر فإن جيب كل زاوية يرتبط من خلال المعادلة \[n_1 . Sin (θ_1)=n_2 . Sin (θ_2)\] \[n_1\] معامل انكسار الوسط الأول \[n_2\] معامل انكسار الوسط الثاني \[θ_1\] زاوية السقوط \[θ_2\] زاوية الإنكسار

🔍 مثال حسابي:

عندما ينتقل الضوء من الهواء (n=1) إلى الماء (n=1.33) بزاوية سقوط 30°:
\[ sin(θ₂) = \frac{(1 × sin(30°))} {1.33} ≈ 0.3759\] θ₂ ≈ 22°

المحاكاة التفاعلية

معامل انكسار الوسط الأول (n₁):

معامل انكسار الوسط الثاني (n₂):

زاوية السقوط (θ₁ بالدرجات):

إجراء الحساب

النتائج:

التطبيقات العملية

1. الألياف البصرية

تستخدم ظاهرة الانعكاس الكلي في نقل البيانات عبر الألياف الزجاجية بنسبة فقدان طاقة ضئيلة

2. المناظير الطبية

تستعمل في التنظير الداخلي لفحص الأعضاء الداخلية بدون جراحة

3. العواكس الضوئية

تستخدم في إشارات المرور والدراجات لعكس الضوء بفعالية

4. تقنيات التصوير

تطبيقات في المجاهر الضوئية المتقدمة والتصوير الطبي

معامل الإنكسار

هي النسبة بين سرعة الضوء في الفراغ إلى سرعة الضوء في ذلك الوسط \[n=\frac{C}{v}\] معامل الإنكسار ليس له وحدة قياس لانها نسبة وهو دوما أكبر من الواحد قيمتة لأن سرعة الضوء في الفراغ دوما هي الأكبر

قانون سنل
في هذه المحاكاة طبق قانون سنل وتحقق من صحة القانون غير كل مرة الوسط وحدد زاوية السقوط والإنكسار ومعامل انكسار الوسط الأول ومعامل انكسار والثاني وطبق قانون سنل وتحقق من المساواة




في هذه المحاكاة غير معامل الانكسار من خلال المحرك على اليمين و إحسب معامل الإنكسار والزاوية التي خرج منها الشعاع

الزاوية الحرجة والانعكاس الكلي

أسقط ضوء من وسط ذو معامل إنكسار أكبر إلى وسط ذي معامل إنكسار أقل وقارن بين زاوية السقوط والانكسار

زاوية السقوط ( أكبر - أصغر) زاوية الإنكسار

قم بزيادة زاوية السقوط حتى تصل إلى زاوية انكسار مقدارها 90 درجة عندها نسمي

زاوية السقوط التي تقابل زاوية إنكسار مقداها 90 درجة بالزاوية الحرجة ويرمز لها بالرمز \[θ_C\]

\[n_1 . Sin (θ_1)=n_2 . Sin (θ_2)\] \[n_1 . Sin (θ_C)=n_2 . Sin (90)\] \[ Sin (θ_C)=\frac{n_2}{n_1}\] طبق في هذه المحاكاة جساب الزاوية الحرجة وتوقع كم قيمة الزاوية التي يحدث بها انعكاس كلي

حساب الزاوية الحرجة

معامل انكسار الوسط الأول (n₁): معامل انكسار الوسط الثاني (n₂): احسب الزاوية الحرجة

محاكاة الانعكاس الكلي

زاوية السقوط (بالدرجات): تحقق من حدوث الانعكاس الكلي

مثال محلول

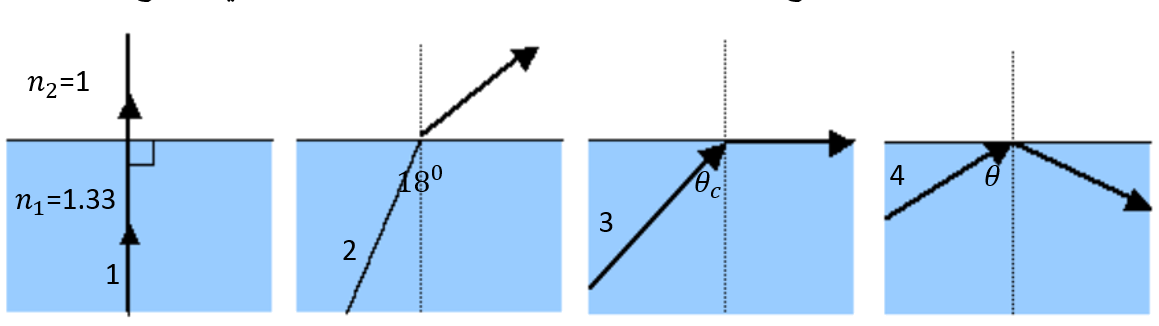
في الشكل أدناه يوجد أربع حالات لسقوط الضوء من الماء إلى الهواء

الشعاع 1 لم يحدث له انكسار لماذا

أحسب زاوية الانكسار للشعاع 2

أحسب الزاوية الحرجة للشعاع 3

لماذا حدث انعكاس كلي للشعاع 4

اضغط هنا تظهر طريقة الحل

المصدر
https:https://www.showmethephysics.com/home/notes/waves/waveLessons2.htm اكتب تعليقا واذا كان هناك خطأ اكتبه وحدد مكانه Write a comment, and if there is mistake, write and specify its location

No comments:

Post a Comment