Physics
📄 اطبع pdf
00971504825082
حفظ كمية الحركة الخطية والتصادمات
هناك أنواع مختلفة من التصادمات منها تام المرونة وتصادم لا مرن وتصادم لا مرن تماما
ومهما كان نوع التصادم فإن كمية الحركة تبقى محفوظة
تصادم مرن في بعد واحد
كمية الحركة محفوظة
\[\vec {P_{i1}}+\vec{P_{i2}}=\vec {P_{f1}}+\vec {P_{f2}}\]
الطاقة الحركية قبل التصادم لكلا الجسمين تساوي الطاقة الحركية للكلا الجسمين بعد التصادم
\[K_{i1}+K_{i2}=K_{f1}+K_{f2}\]
قبل التصادم.....\[m_1= 1 Kg , 𝜗_{i1} =10 m/s\]
\[m_2= 2 Kg , 𝜗_{i2} =-10 m/s\]
بعد التصادم.....\[m_1= 1 Kg , 𝜗_{f1} =- 16.67 m/s\]
\[m_2= 2 Kg , 𝜗_{f2} =3.33 m/s\]
\[m_1.\vec {𝜗_{i1}}+m_2.\vec {𝜗_{i2}}=m_1.\vec {𝜗_{f1}}+m_2.\vec {𝜗_{f1}}\]
\[1 ×10 + 2 ×(- 10 ) = 1 × ( -16.67 ) + 2 ×3.33 \]
\[-10 \frac{Kg .m}{S} =-10 \frac{Kg .m}{S}\]
\[\frac{1}{2}m_1.{𝜗_{i1}}^2+\frac{1}{2}m_2.{𝜗_{i2}}^2=\frac{1}{2}m_1.{𝜗_{f1}}^2+\frac{1}{2}m_2.{𝜗_{f2}}^2\]
\[\frac{1}{2}×1 ×10^2 +\frac{1}{2}× 2 ×(- 10 )^2 = \frac{1}{2}× 1 × ( -16.67 ) + \frac{1}{2}×2 ×(3.33)^2 \]
\[-10 \frac{Kg .m}{S} =-10 \frac{Kg .m}{S}\]
تصادم لا مرن تماما في بعد واحد
يلتحم الجسمين بعد التصادم ويصبح كلاهما جسم واحد
كمية الحركة محفوظة
\[\vec {P_{i1}}+\vec {P_{i2}}=\vec {P_{f}}\]
الطاقة الحركية قبل التصادم لكلا الجسمين أكبر من الطاقة الحركية للكلا الجسمين بعد التصادم
\[K_{i1}+K_{i2}>K_{f}\]
قبل التصادم.....m1= 1 kgm , 𝜗i1 =10 m/s
m2 = 1
kg ,𝜗i2 =-30 m/s
بعد التصادم.....m1 + m2 = 2 kg , 𝜗f =- 10 m/s
\[m_1.\vec{𝜗_{i1}}+m_2.\vec {𝜗_{i2}}=[m_1+m_2].\vec {𝜗_{f}}\]
\[1 x10 + 1 x(- 30 ) = ( 1 + 1 ) x (- 10 )\]
\[-20 \frac{Kg .m}{S} =-20 \frac{Kg .m}{S}\]
\[\frac{1}{2}m_1.{𝜗_{i1}}^2+\frac{1}{2}m_2.{𝜗_{i2}}^2>\frac{1}{2}[m_1+m_2]{𝜗_{f}}^2\]
\[\frac{1}{2}×1 ×10^2 +\frac{1}{2}× 1 ×(- 30 )^2 > \frac{1}{2}×[1+1](-10)^2\]
\[500 \frac{Kg .m^2}{S^2} >100 \frac{Kg .m^2}{S^2}\]
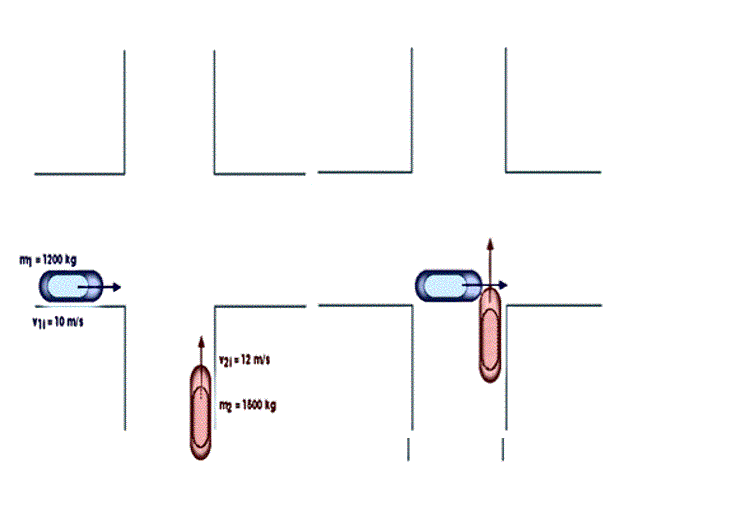
تصادم في بعدين
كمية الحركة محفوظة
\[\vec {P_{i1}}+\vec {P_{i2}}=\vec {P_{f1}}+\vec {P_{f2}}\]
قبل التصادم.\[m_1= 1.5 Kg \;\;\;\;\;\;\;\ ,\;\;\;\;\;\;\;\ 𝜗_{i1} =15 m/s\]
\[m_2 = 1
Kg \;\;\;\;\;\;\;\ ,𝜗_{i2} =0 m/s\]
بعد التصادم\[m_1= 1.5 Kg \;\;\;\;\;\;\;\ , \;\;\;\;\;\;\;\ 𝜗_f =8.66 m/s\;\;\;\;\;\;\;\ ,\;\;\;\;\;\;\;\ 𝜃= 30^0\]شمال الشرق
\[m_2 = 1 Kg \;\;\;\;\;\;\;\ ,\;\;\;\;\;\;\;\ 𝜗_f =13 m/s \;\;\;\;\;\;\;\ ,\;\;\;\;\;\;\;\ 𝜃= 330^0\]جنوب الشرق
\[\vec P_{i1X}+\vec P_{i2X}=\vec P_{f1X}+\vec P_{f2X}\]
\[1.5 ×15 + 1 ×0 = 1.5 ×8.66 × Cos 30 + 1 × 13 × Cos 330 \]
\[22.5 \frac{Kg .m}{S} =22.5 \frac{Kg .m}{S}\]
\[P_{i1Y}+P_{i2Y}=P_{f1Y}+P_{f2Y}\]
\[1.5 ×0 + 1 ×0 = 1.5 x8.66 × Sin 30 + 1 × 13 × Sin 330 \]
\[0.0 \frac{Kg .m}{S} =0.0 \frac{Kg .m}{S}\]
التصادم المرن
يحدث عندما لا يوجد إحتكاك
في التصادم المرن الطاقة الحركية محفوظة
\[K_{i1X}+K_{i2X}=K_{f1X}+K_{f2X}\]
\[\frac{1}{2}m_1.{𝜗_{i1X}}^2+\frac{1}{2}m_2.{𝜗_{i2X}}^2=\frac{1}{2}m_1.{𝜗_{f1X}}^2+\frac{1}{2}m_2.{𝜗_{f2X}}^2\;\;\;\;{1} \]
\[K_{i1Y}+K_{i2Y}=K_{f1Y}+K_{f2Y}\]
\[\frac{1}{2}m_1.{𝜗_{i1Y}}^2+\frac{1}{2}m_2.{𝜗_{i2Y}}^2=\frac{1}{2}m_1.{𝜗_{f1Y}}^2+\frac{1}{2}m_2.{𝜗_{f2Y}}^2\;\;\;\;{1} \]
وكمية الحركة محفوظة
\[P_{i1X}+P_{i2X}=P_{f1X}+P_{f2X}\]
\[m_1.𝜗_{i1X}+m_2.𝜗_{i2X}=m_1.𝜗_{f1X}+m_2.𝜗_{f1X}\\;\;\;\;{2} \]
\[P_{i1Y}+P_{i2Y}=P_{f1Y}+P_{f2Y}\]
\[m_1.𝜗_{i1Y}+m_2.𝜗_{i2Y}=m_1.𝜗_{f1Y}+m_2.𝜗_{f1Y}\\;\;\;\;{2} \]
من خلال حل المعادلتين حل مشترك
\[𝜗_{f1X}=[\frac{m_1-m_2}{m_1+m_2}]𝜗_{i1X}+[\frac{2m_2}{m_1+m_2}]𝜗_{i2X}\]
\[𝜗_{f2X}=.[\frac{2m_1}{m_1+m_2}]𝜗_{i1X}+[\frac{m_2-m_1}{m_1+m_2}]𝜗_{i2X}.\]
في هذه المحاكاة المطلوب تحديد صحة نوع التصادم
الأفقي إن الزاوية التي تصنعها الكرة الوردية بعد التصادم مع المحور الأفقي
600 فوق المحور
إن الزاوية التي تصنعها الكرة الخضراء بعد التصادم مع المحور الأفقي
490تحت المحور
أحسب كمية الحركة قبل وبعد التصادم تذكر أن التصادم يتم في بعدين
أحسب الطاقة الحركية قبل وبعد التصادم
ماذا تستنتج
1
منضدة هوائية يتحرك عليها ركابين كتلة الركاب الأول 0.6 كيلو جرام يتحرك بسرعة
10 m/s
إلى اليسار
بينما يتحرك الركاب الأخر الذي كتلتة 0.4 كيلو جرام بسرعة
20 m/s
نحو اليمين
يتصادم الاثنان بمرونة . ما سرعة كل منهما بعد التصادم
اضغط هنا تظهر طريقة الحل
أختر الإجابة الصحيحة
حالة خاصة قد يكون أحد الجسمين قبل التصادم كان ساكن
أو قد يكون الجسمين لهما نفس الكتلة
\[ 𝜗_{i1}= 0.0 \]
السؤال ما هي العلاقة المعبرة عن سرعة الجسمين بعد التصادم
\[𝜗_{f1X}=[\frac{2m_2}{m_1+m_2}]𝜗_{i2X}\]
\[𝜗_{f2X}=[\frac{m_2-m_1}{m_1+m_2}]𝜗_{i2X}.\]
وإذا كان الجسمين لهما نفس الكتلة
\[ 𝜗_{𝑓1,𝑥} = 𝜗_{i2,𝑥} , 𝜗_{𝑓2,𝑥} = 𝜗_{i1,𝑥}\]
التصادم اللا مرن تماما
معلومات مفيدة: التصادم اللا مرن تماما
يحدث عندما يلتحم الجسمين ويصبح كلاهما جسم واحد
في التصادم اللا مرن الطاقة الحركية غير محفوظة
Ki1+Ki2≠
Kf
و لكن كمية الحركة تكون محفوظة
pi1+pi2=pf
m1 vi1 + m2
vi2 =( m1
+ m2)
vf
في هذه المحاكاة المطلوب تحديد صحة نوع التصادم
أحسب كمية الحركة قبل وبعد إلتحام الجسمين تذكر أن التصادم يتم في بعد واحد
ماذا تستنتج
غير كتل الأجسام وسرعتها وقم بالحساب كل مرة
2
حدث تصادم بين سيارتين عند تقاطع كما هو موضح أدناه. الاصطدام أدى إلى إلتحام السيارتين معا
أحسب السرعة المشتركة للسيارتين بعد الإلتحام
اضغط هنا تظهر طريقة الحل
أختر الإجابة الصحيحة
المصدر
https://www.showmethephysics.com/home/animations3/ModphysSims.htm
🧮 Calculator
حفظ كمية الحركة الخطية والتصادمات |
هناك أنواع مختلفة من التصادمات منها تام المرونة وتصادم لا مرن وتصادم لا مرن تماما
ومهما كان نوع التصادم فإن كمية الحركة تبقى محفوظة
تصادم مرن في بعد واحد
كمية الحركة محفوظة
\[\vec {P_{i1}}+\vec{P_{i2}}=\vec {P_{f1}}+\vec {P_{f2}}\] الطاقة الحركية قبل التصادم لكلا الجسمين تساوي الطاقة الحركية للكلا الجسمين بعد التصادم
\[K_{i1}+K_{i2}=K_{f1}+K_{f2}\]
تصادم لا مرن تماما في بعد واحد
يلتحم الجسمين بعد التصادم ويصبح كلاهما جسم واحد
كمية الحركة محفوظة
\[\vec {P_{i1}}+\vec {P_{i2}}=\vec {P_{f}}\]
الطاقة الحركية قبل التصادم لكلا الجسمين أكبر من الطاقة الحركية للكلا الجسمين بعد التصادم
\[K_{i1}+K_{i2}>K_{f}\]
تصادم في بعدين
كمية الحركة محفوظة
\[\vec {P_{i1}}+\vec {P_{i2}}=\vec {P_{f1}}+\vec {P_{f2}}\]
قبل التصادم.\[m_1= 1.5 Kg \;\;\;\;\;\;\;\ ,\;\;\;\;\;\;\;\ 𝜗_{i1} =15 m/s\]
\[m_2 = 1
Kg \;\;\;\;\;\;\;\ ,𝜗_{i2} =0 m/s\]
بعد التصادم\[m_1= 1.5 Kg \;\;\;\;\;\;\;\ , \;\;\;\;\;\;\;\ 𝜗_f =8.66 m/s\;\;\;\;\;\;\;\ ,\;\;\;\;\;\;\;\ 𝜃= 30^0\]شمال الشرق
\[m_2 = 1 Kg \;\;\;\;\;\;\;\ ,\;\;\;\;\;\;\;\ 𝜗_f =13 m/s \;\;\;\;\;\;\;\ ,\;\;\;\;\;\;\;\ 𝜃= 330^0\]جنوب الشرق
\[\vec P_{i1X}+\vec P_{i2X}=\vec P_{f1X}+\vec P_{f2X}\]
\[1.5 ×15 + 1 ×0 = 1.5 ×8.66 × Cos 30 + 1 × 13 × Cos 330 \]
\[22.5 \frac{Kg .m}{S} =22.5 \frac{Kg .m}{S}\]
\[P_{i1Y}+P_{i2Y}=P_{f1Y}+P_{f2Y}\]
\[1.5 ×0 + 1 ×0 = 1.5 x8.66 × Sin 30 + 1 × 13 × Sin 330 \]
\[0.0 \frac{Kg .m}{S} =0.0 \frac{Kg .m}{S}\]
منضدة هوائية يتحرك عليها ركابين كتلة الركاب الأول 0.6 كيلو جرام يتحرك بسرعة أختر الإجابة الصحيحة يحدث عندما يلتحم الجسمين ويصبح كلاهما جسم واحد
في التصادم اللا مرن الطاقة الحركية غير محفوظة
Ki1+Ki2≠
Kf
و لكن كمية الحركة تكون محفوظة
pi1+pi2=pf
m1 vi1 + m2
vi2 =( m1
+ m2)
vf
حدث تصادم بين سيارتين عند تقاطع كما هو موضح أدناه. الاصطدام أدى إلى إلتحام السيارتين معا أختر الإجابة الصحيحة
قبل التصادم.....\[m_1= 1 Kg , 𝜗_{i1} =10 m/s\]
\[m_2= 2 Kg , 𝜗_{i2} =-10 m/s\]
بعد التصادم.....\[m_1= 1 Kg , 𝜗_{f1} =- 16.67 m/s\]
\[m_2= 2 Kg , 𝜗_{f2} =3.33 m/s\]
\[m_1.\vec {𝜗_{i1}}+m_2.\vec {𝜗_{i2}}=m_1.\vec {𝜗_{f1}}+m_2.\vec {𝜗_{f1}}\]
\[1 ×10 + 2 ×(- 10 ) = 1 × ( -16.67 ) + 2 ×3.33 \]
\[-10 \frac{Kg .m}{S} =-10 \frac{Kg .m}{S}\]
\[\frac{1}{2}m_1.{𝜗_{i1}}^2+\frac{1}{2}m_2.{𝜗_{i2}}^2=\frac{1}{2}m_1.{𝜗_{f1}}^2+\frac{1}{2}m_2.{𝜗_{f2}}^2\]
\[\frac{1}{2}×1 ×10^2 +\frac{1}{2}× 2 ×(- 10 )^2 = \frac{1}{2}× 1 × ( -16.67 ) + \frac{1}{2}×2 ×(3.33)^2 \]
\[-10 \frac{Kg .m}{S} =-10 \frac{Kg .m}{S}\]
m2 = 1
kg ,𝜗i2 =-30 m/s
\[m_1.\vec{𝜗_{i1}}+m_2.\vec {𝜗_{i2}}=[m_1+m_2].\vec {𝜗_{f}}\]
\[1 x10 + 1 x(- 30 ) = ( 1 + 1 ) x (- 10 )\]
\[-20 \frac{Kg .m}{S} =-20 \frac{Kg .m}{S}\]
\[\frac{1}{2}m_1.{𝜗_{i1}}^2+\frac{1}{2}m_2.{𝜗_{i2}}^2>\frac{1}{2}[m_1+m_2]{𝜗_{f}}^2\]
\[\frac{1}{2}×1 ×10^2 +\frac{1}{2}× 1 ×(- 30 )^2 > \frac{1}{2}×[1+1](-10)^2\]
\[500 \frac{Kg .m^2}{S^2} >100 \frac{Kg .m^2}{S^2}\]
يحدث عندما لا يوجد إحتكاك
في التصادم المرن الطاقة الحركية محفوظة
\[K_{i1X}+K_{i2X}=K_{f1X}+K_{f2X}\]
\[\frac{1}{2}m_1.{𝜗_{i1X}}^2+\frac{1}{2}m_2.{𝜗_{i2X}}^2=\frac{1}{2}m_1.{𝜗_{f1X}}^2+\frac{1}{2}m_2.{𝜗_{f2X}}^2\;\;\;\;{1} \]
\[K_{i1Y}+K_{i2Y}=K_{f1Y}+K_{f2Y}\]
\[\frac{1}{2}m_1.{𝜗_{i1Y}}^2+\frac{1}{2}m_2.{𝜗_{i2Y}}^2=\frac{1}{2}m_1.{𝜗_{f1Y}}^2+\frac{1}{2}m_2.{𝜗_{f2Y}}^2\;\;\;\;{1} \]
وكمية الحركة محفوظة
\[P_{i1X}+P_{i2X}=P_{f1X}+P_{f2X}\]
\[m_1.𝜗_{i1X}+m_2.𝜗_{i2X}=m_1.𝜗_{f1X}+m_2.𝜗_{f1X}\\;\;\;\;{2} \]
\[P_{i1Y}+P_{i2Y}=P_{f1Y}+P_{f2Y}\]
\[m_1.𝜗_{i1Y}+m_2.𝜗_{i2Y}=m_1.𝜗_{f1Y}+m_2.𝜗_{f1Y}\\;\;\;\;{2} \]
من خلال حل المعادلتين حل مشترك
\[𝜗_{f1X}=[\frac{m_1-m_2}{m_1+m_2}]𝜗_{i1X}+[\frac{2m_2}{m_1+m_2}]𝜗_{i2X}\]
\[𝜗_{f2X}=.[\frac{2m_1}{m_1+m_2}]𝜗_{i1X}+[\frac{m_2-m_1}{m_1+m_2}]𝜗_{i2X}.\]
الأفقي إن الزاوية التي تصنعها الكرة الوردية بعد التصادم مع المحور الأفقي
600 فوق المحور
إن الزاوية التي تصنعها الكرة الخضراء بعد التصادم مع المحور الأفقي
490تحت المحور
أحسب كمية الحركة قبل وبعد التصادم تذكر أن التصادم يتم في بعدين
أحسب الطاقة الحركية قبل وبعد التصادم
ماذا تستنتج
10 m/s
إلى اليسار
بينما يتحرك الركاب الأخر الذي كتلتة 0.4 كيلو جرام بسرعة
20 m/s
نحو اليمين
يتصادم الاثنان بمرونة . ما سرعة كل منهما بعد التصادم
اضغط هنا تظهر طريقة الحل
حالة خاصة قد يكون أحد الجسمين قبل التصادم كان ساكن
أو قد يكون الجسمين لهما نفس الكتلة
\[ 𝜗_{i1}= 0.0 \]
السؤال ما هي العلاقة المعبرة عن سرعة الجسمين بعد التصادم
\[𝜗_{f1X}=[\frac{2m_2}{m_1+m_2}]𝜗_{i2X}\]
\[𝜗_{f2X}=[\frac{m_2-m_1}{m_1+m_2}]𝜗_{i2X}.\]
وإذا كان الجسمين لهما نفس الكتلة
\[ 𝜗_{𝑓1,𝑥} = 𝜗_{i2,𝑥} , 𝜗_{𝑓2,𝑥} = 𝜗_{i1,𝑥}\]
معلومات مفيدة: التصادم اللا مرن تماما
في هذه المحاكاة المطلوب تحديد صحة نوع التصادم
أحسب كمية الحركة قبل وبعد إلتحام الجسمين تذكر أن التصادم يتم في بعد واحد
ماذا تستنتج
غير كتل الأجسام وسرعتها وقم بالحساب كل مرة
أحسب السرعة المشتركة للسيارتين بعد الإلتحام
اضغط هنا تظهر طريقة الحل
المصدر
https://www.showmethephysics.com/home/animations3/ModphysSims.htm
No comments:
Post a Comment