Search

 
 

📄 اطبع pdf
00971504825082

<<<طاقة الوضع>>>


وهي الطاقة التي يختزنها الجسم وهناك انواع مختلفة
كما تم إظهاره في الصور هل يمكن أن تحدد نوع الطاقة المختزنة في كل صورة
سوف ندرس الأن نوعين منها وهي طاقة الوضع الجذبية وطاقة الوضع المرونية

طاقة الوضع الجذبية

تجربة تفاعلية لطاقة الوضع الجذبية

\[ GPE = U_G = m \cdot g \cdot h\]

طاقة الوضع الجذبية هي الطاقة التي يختزنها جسم نتيجة موضعه من مستوى إسناد صفري. في هذه المحاكاة سوف ندرس العوامل المؤثرة على طاقة الوضع الجذبية.

يرمز لطاقة الوضع الجذبية بالرموز التالية:\[( GPE ) \;\;\; ( UG )\] وتقدر بوحدة الجول \[(J)\].

التجربة 1: دراسة اعتماد طاقة الوضع الجذبية على الارتفاع

غير ارتفاع الجسم مع بقاء الكتلة ومجال الجاذبية ثابت وحدد كل مرة طاقة الوضع الجذبية.

طاقة الوضع \[ GPE = U (J) \] الارتفاع \[ h (m) \] مجال الجاذبية \[ g (m/s^2) \] الكتلة \[ m (kg) \] رقم المحاولة
200 J 10 m \( g = 10 m/s^2 \) \( m = 2 kg \) 1

ماذا تستنتج؟

\[..............................................................\]
الاستنتاج الصحيح:

طاقة الوضع الجذبية تتناسب طردياً مع الارتفاع. عندما يزيد الارتفاع تزيد طاقة الوضع الجذبية، وعندما يقل الارتفاع تقل طاقة الوضع الجذبية (بافتراض ثبات الكتلة ومجال الجاذبية).

التجربة 2: دراسة اعتماد طاقة الوضع الجذبية على كتلة الجسم

غير كتلة الجسم مع بقاء الارتفاع ومجال الجاذبية ثابت وحدد كل مرة طاقة الوضع الجذبية.

طاقة الوضع \[ GPE = U (J) \] الكتلة \[ m (kg) \] مجال الجاذبية \[ g (m/s^2) \] الارتفاع \[ h (m) \] رقم المحاولة
200 J 2 kg \[ g = 10 m/s^2 \] \[ h = 10 m \] 1

ماذا تستنتج؟

\[..............................................................\]
الاستنتاج الصحيح:

طاقة الوضع الجذبية تتناسب طردياً مع كتلة الجسم. عندما تزيد الكتلة تزيد طاقة الوضع الجذبية، وعندما تقل الكتلة تقل طاقة الوضع الجذبية (بافتراض ثبات الارتفاع ومجال الجاذبية).

التجربة 3: دراسة اعتماد طاقة الوضع الجذبية على مجال الجاذبية

غير مجال الجاذبية مع بقاء الارتفاع والكتلة ثابت وحدد كل مرة طاقة الوضع الجذبية.

طاقة الوضع \[ GPE = U (J) \] مجال الجاذبية\[ g (m/s^2) \] الكتلة \[ m (kg) \] الارتفاع \[ h (m) \] رقم المحاولة
200 J 10 m/s² \( m = 2 kg \) \( h = 10 m \) 1

ماذا تستنتج؟

\[..............................................................\]
الاستنتاج الصحيح:

طاقة الوضع الجذبية تتناسب طردياً مع مجال الجاذبية. عندما يزيد مجال الجاذبية تزيد طاقة الوضع الجذبية، وعندما يقل مجال الجاذبية تقل طاقة الوضع الجذبية (بافتراض ثبات الكتلة والارتفاع).


\[GPE=m.g.h\]


\[1 \star\]

برميل نفط كتلته 100 كيلوجرام يمتلك طاقة وضع مقدارها
\[2900\;j\]
فإن ارتفاع البرميل عن سطح الأرض يعادل \[g=9.81\frac{m}{s^2}\]


اختر الإجابة الصحيحة

A
h=2.25 m
B
h=2.95 m
C
h=1.58 m
D
h=1.96 m
  • اضغط هنا تظهر طريقة الحل
    • \[2\star\]

    كم يكون التغير في طاقة الوضع للوح خشبي كتلتة 30 كيلوجرام مرفوع فوق رأس الرجل على ارتفاع 2.2 متر ويتحرك به مسافة 12 متر نحو اليمين \[g=9.81\frac{m}{s^2}\]

    أختر الإجابة الصحيحة

    A
    ∆ PEG=435.7 J
    B
    ∆ PEG= 647.5 J
    C
    ∆ PEG=2884.1 J
    D
    ∆ PEG=0 J
  • اضغط هنا تظهر طريقة الحل

    • طاقة الوضع المرونية
    طاقة الوضع المرونية أو الطاقة الكامنة هي الطاقة المخزنة داخل الأجسام، والتي تعتمد على وضع جزيئات الجسم نسبة إلى
    جزيئاتة الأخرى في النظام ذاته
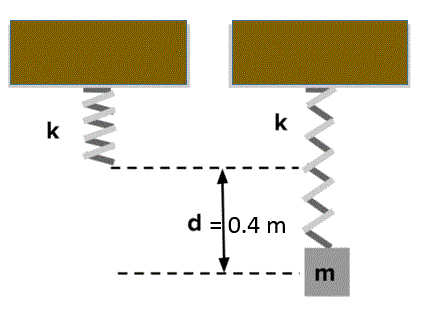
    الزنبركات من الأجسام المرنة تمتلك طاقة وضع مرونية إذا تم ضغطها أو شدها



    ( pEs أو us )يرمز لطاقة الوضع الجذبية بالرمز
    وتقدر بوحدة الجول

    إذا أثرنا بقوة شد على زنبرك فإن الزنبرك سوف يستطيل و حسب المعلومات السابقة تم بذل شغل على الزنبرك
    هذا الشغل قد تحول إلى طاقة وضع مرونية وكلما زدنا من قوة الشد تزداد الأستطالة وتزداد طاقة الوضع للزنبرك
    من خلال حساب الشغل المبذول على الزنبلرك والذي يعادل المساحة المحصورة تحت المنحنى والذي
    يعادل طاقة الوضع المرونية

    تجربة قانون هوك - معمل الفيزياء التفاعلي

    إذا أثرنا بقوة شد على زنبرك فإن الزنبرك سوف يستطيل و حسب المعلومات السابقة تم بذل شغل على الزنبرك.

    هذا الشغل قد تحول إلى طاقة وضع مرونية وكلما زدنا من قوة الشد تزداد الأستطالة وتزداد طاقة الوضع للزنبرك.

    من خلال حساب الشغل المبذول على الزنبرك والذي يعادل المساحة المحصورة تحت المنحنى والذي يعادل طاقة الوضع المرونية.

    في هذه المحاكاة علق كتل مختلفة في النابض وحدد الإزاحة كل مرة واملأ البيانات في الجدول التالي.

    في هذة المحاكاة علق كتل مختلفة في النابض \[m_1=10 g\;\;\;\; ,\;\;\;\; m_2=20 g\;\;\;\; ,\;\;\;\;m_3=60 g\;\;\;\; ,\;\;\;\;m_4=30 g \]

    وحدد الإزاحة كل مرة واملأ البيانات في الجدول التالي

    طاقة الوضع المرنة
    \[PEs = \frac{1}{2}k(ΔL)^2 (J)\]

    الإستطالة
    \[ΔL = L_2 - L_1 (m)\]

    القوة
    \[F = m \cdot g (N)\]

    عجلة الجاذبية
    \[g (m/s^2)\]

    الكتلة
    \[m (kg)\]

    رقم المحاولة

    \[PEs = .... J\]

    m

    \[F = .... N\]

    \[g = 10 m/s^2\]

    \[m_1 = 0.01 kg\]

    1

    \[PEs = .... J\]

    m

    \[F = .... N\]

    \[g = 10 m/s^2\]

    \[m_2 = 0.02 kg\]

    2

    \[PEs = .... J\]

    m

    \[F = .... N\]

    \[g = 10 m/s^2\]

    \[m_3 = 0.06 kg\]

    3

    \[PEs = .... J\]

    m

    \[F = .... N\]

    \[g = 10 m/s^2\]

    \[m_4 = 0.03 kg\]

    4

    حساب ثابت هوك من المنحنى البياني

    ثابت هوك (k) يساوي ميل الخط البياني (القوة ÷ الإزاحة)

    أدخل قيمة ثابت هوك المستنتج من المنحنى: N/m

    حساب طاقة الوضع المرونية

    طاقة الوضع المرونية= المساحة المحصورة تحت المنحنى \[ PEs = \frac{1}{2} F.(ΔL) \]

    احسب قيمة طاقة الوضع المرونية للكتلة الرابعة: J



    مثال محلول
    تم رسم العلاقة بين قوة الشد والاستطالة لزنبركين ايهما أكثر صلابة


    \[K = 𝑚=(\frac{𝐹_2−𝐹_1}{𝐿_2−𝐿_1 })\] كلما زاد الميل زادت قيمة ثابت هوك ( A) وزيادة الثابت يعني أن الزنبرك أكثر صلابة هو

    \[8\]

    نابض ثابت الصلابة له \[k=20 \frac{N}{m}\] فإن مقدار طاقة الوضع المرونة عندما يستطيل بمقدار \[0.4\;m\]تعادل

    أختر الإجابة الصحيحة

    A
    𝑃𝐸𝑆=4 j
    B
    𝑃𝐸𝑆=1.6 j
    C
    𝑃𝐸𝑆=2 j
    D
    𝑃𝐸𝑆=2.4 j
  • اضغط هنا تظهر طريقة الحل

    • المصدر https://www.seilias.gr/go-lab/html5/potentialEnergy.plain.html

    https://www.showmethephysics.com/home/notes/energy/ElasticPE.htm

    اكتب تعليقا واذا كان هناك خطأ اكتبه وحدد مكانه Write a comment, and if there is mistake, write and specify its location

    No comments:

    Post a Comment

    🧮 Calculator
    🗑️
    ✏️ قلم